当前位置:网站首页>Linear algebra study notes 4-4: Solving the inhomogeneous system of linear equations Ax=b, looking at the equations from the perspective of rank
Linear algebra study notes 4-4: Solving the inhomogeneous system of linear equations Ax=b, looking at the equations from the perspective of rank
2022-08-07 04:58:00 【Insomnia_X】
A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b与 A x = 0 \mathbf A \boldsymbol x=\boldsymbol 0 Ax=0的区别在于:
- 对于齐次线性方程组 A x = 0 \mathbf A \boldsymbol x=\boldsymbol 0 Ax=0,No matter how the left coefficient matrix is row transformed,The coefficient on the right is always 0 \boldsymbol 0 0;
A x = 0 \mathbf A \boldsymbol x=\boldsymbol 0 Ax=0必定有解,It's just that the solution space may be large or small(唯一零解?无穷解?) - 然而对于 A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b,消元时,右侧的 b \boldsymbol b band the left-hand coefficient matrix A \mathbf A ATransform together,We need to consider augmented matrices [ A b ] \begin{bmatrix}\mathbf A&\boldsymbol b\end{bmatrix} [Ab]
A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b可能无解,there may also be a solution;A solution may be the only solution/无穷解
A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b有解,一定要保证:Once the linear combination of some lines on the left is the full0,The coefficient on the right side must also be0(After elimination, the equation always satisfies"0=0"的约束)
例如, [ A b ] = [ 1 2 2 2 b 1 2 4 6 8 b 2 3 6 8 10 b 3 ] \begin{bmatrix}\mathbf A&\boldsymbol b\end{bmatrix}=\begin{bmatrix}1&2&2&2&b_1\\2&4&6&8&b_2\\3&6&8&10&b_3\end{bmatrix} [Ab]=⎣⎡1232462682810b1b2b3⎦⎤,get after elimination [ 1 2 2 2 b 1 0 0 2 4 b 2 − 2 b 1 0 0 0 0 b 3 − b 2 − b 1 ] \begin{bmatrix}1&2&2&2&b_1\\0&0&2&4&b_2-2b_1\\0&0&0&0&b_3-b_2-b_1\end{bmatrix} ⎣⎡100200220240b1b2−2b1b3−b2−b1⎦⎤,则必须满足 b 3 − b 2 − b 1 = 0 b_3-b_2-b_1=0 b3−b2−b1=0
A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b有解的条件
- for augmented matrices [ A b ] \begin{bmatrix}\mathbf A&\boldsymbol b\end{bmatrix} [Ab],若 A \mathbf A AThe linear combination of certain lines yields the full0行,对应的 b \boldsymbol b bside is also0,则方程 A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b有解
Why is it so certain that the equation has a solution??
First of all this is saying,There is no between the equations“互相矛盾”(Didn't show up after disappearing"0=1")
其次,We start solving from the last pivot,Bring back up,The unknowns must be solved according to the constraints of the equation,But it is not certain how many solutions there are.
- 仅当 A \mathbf A A的列空间 C ( A ) C(\mathbf A) C(A)包含向量 b \boldsymbol b b时,方程 A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b有解
[矩阵乘法角度]这就是说,A linear combination of column vectors can be obtained b \boldsymbol b b
[geometric angle]矩阵 A \mathbf A ALinearly transformed space(base is a column vector),包含 b \boldsymbol b b
因此,We can first find the column space,然后判断是否有解
求解 A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b
求解 A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b, A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b的一个特解 + A x = 0 \mathbf A \boldsymbol x=\boldsymbol 0 Ax=0all possible solutions of = A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=ball possible solutions of
具体步骤: A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b使用5-3The elimination method in question gets a special solution, A x = 0 \mathbf A \boldsymbol x=\boldsymbol 0 Ax=0Use the elimination method to obtain the basic solution system and null space,The two can be superimposed
- 原因: x p x_p xp为 A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b的特解, x n x_n xn为 A x = 0 \mathbf A \boldsymbol x=\boldsymbol 0 Ax=0all possible solutions of( A \mathbf A Aall vectors in the null space of),那么有 A x p = b \mathbf A \boldsymbol x_p=\boldsymbol b Axp=b和 A x n = 0 \mathbf A \boldsymbol x_n=\boldsymbol 0 Axn=0,两个方程相加,得到 A ( x p + x n ) = b \mathbf A \boldsymbol {(x_p+x_n)}=\boldsymbol b A(xp+xn)=b,从而所有 ( x p + x n ) \boldsymbol {(x_p+x_n)} (xp+xn)都是方程 A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b的解
- 注意, A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b的解空间一定不是向量空间,因为不含 0 \boldsymbol 0 0向量,This solution space can be understood as: A x = 0 \mathbf A \boldsymbol x=\boldsymbol 0 Ax=0的零空间(向量空间)and equation particular solution vector x p x_p xp的叠加(Zero space for translation,好比y=x到y=x+b的平移)
- its implied meaning:
①若 R a n k ( A ) = n Rank(\mathbf A)=n Rank(A)=n,那么 A x = 0 \mathbf A \boldsymbol x=\boldsymbol 0 Ax=0有唯一零解,则 A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=bonly solution(如果有解)
②若 R a n k ( A ) < n Rank(\mathbf A)<n Rank(A)<n,Then the matrix corresponds to the dimensionality reduction transformation,那么 A x = 0 \mathbf A \boldsymbol x=\boldsymbol 0 Ax=0solution space(dimension greater than zero,An infinite a non-zero solution),进而 A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b的通解= A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b的一个特解 + A x = 0 \mathbf A \boldsymbol x=\boldsymbol 0 Ax=0any linear combination of the fundamental solution system of
From the perspective of rank equation
定义秩 R a n k ( A ) Rank(\mathbf A) Rank(A): m m m行 n n n列的系数矩阵 A \mathbf A AAfter elimination,number of pivots,and must have r ≤ m r\leq m r≤m和 r ≤ n r\leq n r≤n
- If a column full rank R a n k ( A ) = n < m Rank(\mathbf A)=n<m Rank(A)=n<m,那么 A x = 0 \mathbf A \boldsymbol x=\boldsymbol 0 Ax=0有唯一零解,则 A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=bonly solution(如果有解)
原因:这意味着方程 A x = 0 \mathbf A \boldsymbol x=\boldsymbol 0 Ax=0Each column has a pivot,All variables are the main variables,Always be on the right side and equations0,So get the only solution 0 \boldsymbol 0 0,That is, the null space is a point,进一步导致 A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b无解/唯一解 - If the row is full R a n k ( A ) = m < n Rank(\mathbf A)=m<n Rank(A)=m<n,那么对于任意 b \boldsymbol b b, A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b必定有解,且有 n − R a n k ( A ) n-Rank(\mathbf A) n−Rank(A)个自由变量(This is also the number of vectors in the basic solution system/零空间的维数)
原因:This means that after the elimination is complete,左侧的 A \mathbf A Adid not appear in full0行,Therefore, there is no situation where the equations contradict each other.(如"0=1") - 行列满秩/满秩 R a n k ( A ) = n = m Rank(\mathbf A)=n=m Rank(A)=n=m, A x = 0 \mathbf A \boldsymbol x=\boldsymbol 0 Ax=0唯一零解(Null space is a point), A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b有唯一解
理解:After elimination, each row and column has pivot,Then the row least echelon form must be the identity matrix - 若 R a n k ( A ) < n 且 R a n k ( A ) < m Rank(\mathbf A)<n且Rank(\mathbf A)<m Rank(A)<n且Rank(A)<m,Then the matrix corresponds to the dimensionality reduction transformation,那么 A x = 0 \mathbf A \boldsymbol x=\boldsymbol 0 Ax=0有无穷个解,进而 A x = b \mathbf A \boldsymbol x=\boldsymbol b Ax=b有无穷个解
Reduced echelon form from row after elimination R \mathbf R R来看:
- Does the equation have a solution,就要看 R \mathbf R RDoes all appear0行
If there is a whole0行,右边的 b \boldsymbol b b对应为0,才有解;否则无解 - Does the equation have a unique solution or an infinite solution,就要看 R \mathbf R RThe number of free variables in n − r n-r n−r(列数-秩/主元个数)
0free variables, the equation has a unique solution;1more than one free variable,方程有无穷解(How many free variables,Several basic solution system of vector,Thus zero space dimension is few)
specific to each situation:
- R a n k ( A ) = m = n Rank(\mathbf A)=m=n Rank(A)=m=n,行简化阶梯型 R = I \mathbf R=\mathbf I R=I,not complete0行,Equation must have a solution,and the number of free variables is 0 0 0,有唯一解
- R a n k ( A ) = n < m Rank(\mathbf A)=n<m Rank(A)=n<m, R = [ I 0 ] \mathbf R=\begin{bmatrix}\mathbf I\\ \mathbf 0\end{bmatrix} R=[I0],when the corresponding row b \boldsymbol b b为0时方程才有解;若有解,The number of free variables is 0 0 0,唯一解
- R a n k ( A ) = m < n Rank(\mathbf A)=m<n Rank(A)=m<n, R = [ I F ] \mathbf R=\begin{bmatrix}\mathbf I& \mathbf F\end{bmatrix} R=[IF](After rearranging the variables you get this form),not complete0行,Equation must have a solution,The number of free variables is n − r > 0 n-r>0 n−r>0,有无穷解(Zero space, at least, is a straight line)
- R a n k ( A ) < n 且 R a n k ( A ) < m Rank(\mathbf A)<n且Rank(\mathbf A)<m Rank(A)<n且Rank(A)<m, R = [ I F 0 0 ] \mathbf R=\begin{bmatrix}\mathbf I& \mathbf F\\ \mathbf 0&\mathbf 0\end{bmatrix} R=[I0F0],when the corresponding row b \boldsymbol b b为0时方程才有解;若有解,The number of free variables is n − r > 0 n-r>0 n−r>0,有无穷解
总之,
A \mathbf A A的零空间维数 d i m [ N ( A ) ] dim[N(\mathbf A)] dim[N(A)]= A \mathbf A AAfter the elimination of free column number n − R a n k ( A ) n-Rank(\mathbf A) n−Rank(A)
秩 R a n k ( A ) Rank(\mathbf A) Rank(A)=矩阵 A \mathbf A Athe number of pivot columns= A \mathbf A AMaximum number of linearly independent column vectors= A \mathbf A Athe column space dimension of d i m [ C ( A ) ] dim[C(\mathbf A)] dim[C(A)]
秩 R a n k ( A ) Rank(\mathbf A) Rank(A)determines the structure of the solution to the equation(有没有解、有唯一/无穷解)
边栏推荐
- volatile原理
- volatile principle
- [Shader realizes the overall distortion effect of Distortion_Shader Effect Chapter 17]
- Sigrity PowerDC Simulation
- 【毕业设计】基于STM32的自动加油站加油系统 -物联网 单片机 嵌入式
- Golang 作用域的坑
- The fourth virtual camera: who is calling the v4l2_camera_HAL camera driver
- tiup cluster display
- Seq2Seq 粗浅理解
- Through document url for base64;Through image url access to base64;Js file for base64
猜你喜欢

2022 Niu Ke Duo School Six J-Number Game (Simple Reasoning)

M write log to text

How to adjust the game settings of Ark Survival Evolved

线性代数学习笔记2-3补充:抽象向量空间

Project management knowledge points

【TypeScript笔记】03 - TS类型声明文件

小 P 周刊 Vol.14

Detailed explanation of C51 basic functions, interrupt functions and library functions

Quantitative risk control rule development, how to better make policies and rules, catch bad guys
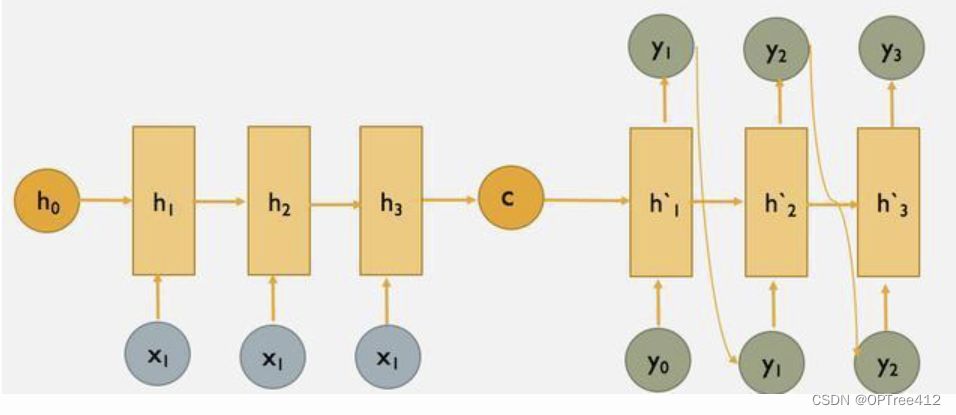
Seq2Seq 粗浅理解
随机推荐
Small P weekly, Vol. 14
npm install encountered Unexpected end of JSON input while parsing near '...onnect": "^2.0.0", "gru" problem solved
线性代数学习笔记3-4:描述线性变换的空间压缩情况(列空间、秩)
How to quickly develop an app?Mini programs + plugins are indispensable
[TypeScript Notes] 02 - TS Advanced Types
STC不同系列单片机的软串口位时间函数差异
【愚公系列】2022年08月 Go教学课程 031-结构体方法
2022牛客多校六 M-Z-Game on grid(动态规划)
typescript85-class组件类型
happens-before rule and thread singleton safety exercise
tiup cluster help
Supplement to Linear Algebra Study Notes 2-3: Abstract Vector Spaces
多线程进阶
tiup cluster enable
聊聊Redis内存优化的7个神技
线性代数学习笔记6-2:行列式的理解、行列式的性质
Backtracking and its Simple Question Example
[SemiDrive source code analysis] [MailBox inter-core communication] 48 - Modify the RPMSG IPCC RPC single transmission data size to 512 bytes (code actual combat part)
Differences in the soft serial port bit time function of different series of STC microcontrollers
关于log4j安全漏洞以及版本替换的记录