pytorch geometric中为何要将稀疏邻接矩阵写成转置的形式adj_t

一开始接触pytorch geometric的小伙伴可能和我有一样的疑问，为何数据中邻接矩阵要写成转置的形式。直到看了源码，我才理解作者这样写，是因为信息传递方式的原因，这里我跟大家分享一下。

edge_index

首先pytorch geometric的边信息可以有两种存储模式，第一种是edge_index，它的shape是[2, N]，其中N是边的数目。第一个N维的元素存储边的原点的信息，称为source，第二个N维的元素存储边的目标点的信息，称为target。举个例子，如果我们有以下这样一张有向图，那么edge_index是这样的: tensor([[1, 2, 3, 4], [0, 0, 0, 0]])，边是(1,0), (2,0), (3,0), (3,0)

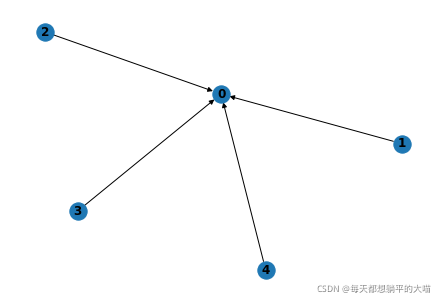
如果以上的图是无向图的话，那么0这个节点也指向1,2,3,4这几个节点，edge_index则应该是的: tensor([[1, 2, 3, 4,0, 0, 0, 0], [0, 0, 0, 0, 1, 2, 3, 4]])，边是(1,0), (2,0), (3,0), (3,0), (0,1), (0,2), (0,3), (0,4)。
edge_index这么写的原因是，在pytorch geometric中，用scatter一类的方式可以很方便地实现，从source到target，这种默认的边传递方式。（当然传递方式你也可以改成从target传递到source。）如果以上你还有不是很明白的地方，那就先记住，边传递的方式是从source到target的，后面在看源码的过程中，会慢慢明白的。

adj_t

pytorch geometric的边信息的第二种存储模式是adj_t，它是一个sparse tensor。这里我们看到作者在adj后面加上了t，说明它是邻接矩阵的转置。为什么要写成转置呢，我们接着上面edge_index讲。
首先我们为什么需要稀疏邻接矩阵，而不是直接用edge_index？那是因为如果可以用稀疏邻接矩阵可以极大地加快计算速度，节约内存。当然我们也有一些避免不了显式边传递的图算法，比如GAT这种需要在边上单独操作的图算法。
将edge_index转换成邻接矩阵的时候，自然而然地会写出以下形式：

adj = SparseTensor(row=edge_index[0], col=edge_index[1], value=...,
                   sparse_sizes=(num_nodes, num_nodes))

但是我们都知道，矩阵计算AW是将行上的邻居的特征聚合的过程，其中A是邻接矩阵，W是特征矩阵。如果是刚接触图算法的小伙伴，我借用了以下一张图，可以看出来，每个节点最终生成的embedding是它在A所在行中邻居对应的特征值的求和，所以本质上是聚合列对应的信息聚到行。图中A只有邻居E，不过可以想一下点D，它有B, C, E三个邻居，因此它的特征是B, C, E三个邻居特征的和，聚合了列中B, C, E对应的信息到行中的D。

那这样就产生了一个问题，edge_index中信息传递是source to target，也就是edge_index[0] to edge_index[1]，而adj中是col到row，这样就产生了不一致的问题。所以在做矩阵计算传递信息的时候，作者将adj转换成adj_t，并且将它作为默认形式，这样就保持了一致。

举例

看一个作者在文档中的关于GIN实现的例子：https://pytorch-geometric.readthedocs.io/en/latest/notes/sparse_tensor.html?highlight=adj_t#memory-efficient-aggregations

from torch_sparse import matmul

class GINConv(MessagePassing):
    def __init__(self):
        super().__init__(aggr="add")

    def forward(self, x, edge_index):
        out = self.propagate(edge_index, x=x)
        return MLP((1 + eps) x + out)

    def message(self, x_j):
        return x_j

    def message_and_aggregate(self, adj_t, x):
        return matmul(adj_t, x, reduce=self.aggr)

可以看到在message_and_aggregate这一步信息传递的过程中，使用的是默认的adj_t。

我正在跟新pytorch geometric系列教程pytorch_geometric代码详解，欢迎大家评论交流。