当前位置:网站首页>[Advanced Mathematics] Advanced Number Arrangement: Common Equivalent Infinitesimals, Derivatives and Differentials, Differential Equations
[Advanced Mathematics] Advanced Number Arrangement: Common Equivalent Infinitesimals, Derivatives and Differentials, Differential Equations
2022-08-07 14:42:00 【JKL27】
一、常见等价无穷小
当 x → 0 x\rightarrow0 x→0 时,
sin x ∼ x \sin x \sim x sinx∼x
tan x ∼ x \tan x\sim x tanx∼x
arcsin x ∼ x \arcsin x \sim x arcsinx∼x
arctan x ∼ x \arctan x \sim x arctanx∼x
e x − 1 ∼ x e^x-1 \sim x ex−1∼x, a x − 1 ∼ x ln a a^x-1 \sim x \ln a ax−1∼xlna
ln ( 1 + x ) ∼ x \ln (1+x) \sim x ln(1+x)∼x, l o g a ( 1 + x ) ∼ x ln a \displaystyle\ log_{a}(1+x) \sim \frac{x}{\ln a} loga(1+x)∼lnax
ln ( x + 1 + x 2 ) ∼ x \displaystyle \ln(x+\sqrt{1+x^2}) \sim x ln(x+1+x2)∼x
( 1 + x ) α − 1 ∼ α x \displaystyle (1+x)^\alpha -1 \sim \alpha x (1+x)α−1∼αx
1 − cos x ∼ 1 2 x 2 \displaystyle \displaystyle 1 - \cos x \sim \frac{1}{2}x^2 1−cosx∼21x2
tan x − x ∼ 1 3 x 3 \displaystyle \tan x-x \sim \frac{1}{3}x^3 tanx−x∼31x3
x − sin x ∼ 1 6 x 3 \displaystyle x-\sin x \sim \frac{1}{6}x^3 x−sinx∼61x3
tan x − sin x ∼ 1 2 x 3 \displaystyle \tan x - \sin x \sim \frac{1}{2}x^3 tanx−sinx∼21x3
arcsin x − x ∼ 1 6 x 3 \displaystyle \arcsin x - x \sim \frac{1}{6}x^3 arcsinx−x∼61x3
x − arctan x ∼ 1 3 x 3 \displaystyle x - \arctan x \sim \frac{1}{3}x^3 x−arctanx∼31x3
当 x → ∞ x \rightarrow \infin x→∞ 时,
lim x → ∞ ( 1 + 1 x ) x = e \large \displaystyle \lim\limits_{x\rightarrow \infin}(1+ \frac{1}{x})^x=e x→∞lim(1+x1)x=e, A trend in parentheses 0 .
二、导数 / 微分
利用导数的定义:
lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x \lim\limits_{\Delta x \rightarrow 0}\dfrac{f(x+\Delta x) - f(x)}{\Delta x} Δx→0limΔxf(x+Δx)−f(x)
lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 \lim\limits_{x\rightarrow x_0}\dfrac{f(x)-f(x_0)}{x-x_0} x→x0limx−x0f(x)−f(x0)
常见函数的导数
| 函数 | 导数 |
|---|---|
| sin x \sin x sinx | d ( sin x ) d x = cos x \displaystyle \cfrac{\text{d}(\sin x)}{\text{d}x}=\cos x dxd(sinx)=cosx |
| cos x \cos x cosx | d ( cos x ) d x = − sin x \dfrac{\text{d}(\cos x)}{\text{d}x}=-\sin x dxd(cosx)=−sinx |
| tan x \tan x tanx | d ( tan x ) d x = sec 2 x \dfrac{\text{d}(\tan x)}{\text{d}x}=\sec^2x dxd(tanx)=sec2x |
| cot x \cot x cotx | d ( cot x ) d x = − csc 2 x \dfrac{\text{d}(\cot x)}{\text{d}x}=-\csc^2 x dxd(cotx)=−csc2x |
| sec x \sec x secx | d ( sec x ) d x = sec x tan x \dfrac{\text{d}(\sec x)}{\text{d}x}=\sec x\tan x dxd(secx)=secxtanx |
| csc x \csc x cscx | d ( csc x ) d x = − csc x cot x \dfrac{\text{d}(\csc x)}{\text{d}x}=-\csc x \cot x dxd(cscx)=−cscxcotx |
| arcsin x \arcsin x arcsinx | d ( arcsin x ) d x = 1 1 − x 2 \displaystyle \frac{\text{d}(\arcsin x)}{\text{d}x} = \frac{1}{\sqrt{1-x^2}} dxd(arcsinx)=1−x21 |
| arccos x \arccos x arccosx | d ( arccos x ) d x = − 1 1 − x 2 \displaystyle \dfrac{\text{d}(\arccos x)}{\text{d}x}=-\dfrac{1}{\sqrt{1-x^2}} dxd(arccosx)=−1−x21 |
| arctan x \arctan x arctanx | d ( arctan x ) d x = 1 1 + x 2 \dfrac{\text{d}(\arctan x)}{\text{d}x} = \dfrac{1}{1+x^2} dxd(arctanx)=1+x21 |
| arccot x \text{arccot}\space x arccot x | d ( arccot x ) d x = − 1 1 + x 2 \dfrac{\text{d}(\text{arccot}\space x)}{\text{d}x} = - \dfrac{1}{1+x^2} dxd(arccot x)=−1+x21 |
双曲函数 和 反双曲函数
函数名 表达式 双曲正弦 sh x \operatorname{sh}x shx sh x = e x − e − x 2 \operatorname{sh} x = \dfrac{e^x-e^{-x}}{2} shx=2ex−e−x 双曲余弦 ch x \operatorname{ch}x chx ch x = e x + e − x 2 \operatorname{ch} x = \dfrac{e^x + e^{-x}}{2} chx=2ex+e−x 双曲正切 th x \operatorname{th}x thx th x = sh x ch x = e x − e − x e x + e − x \operatorname{th} x = \dfrac{\operatorname{sh}x}{\operatorname{ch}x}=\dfrac{e^x-e^{-x}}{e^x+e^{-x}} thx=chxshx=ex+e−xex−e−x 反双曲正弦 arcsh x \operatorname{arcsh}x arcshx arcsh x = ln ( x + x 2 + 1 ) \displaystyle \operatorname{arcsh}x = \ln(x+\sqrt{x^2+1}) arcshx=ln(x+x2+1) 1 反双曲余弦 arcch x \operatorname{arcch}x arcchx arcch x = ln ( x + x 2 − 1 ) \operatorname{arcch}x=\ln(x+\sqrt{x^2-1}) arcchx=ln(x+x2−1) 反双曲正切 arcth x \operatorname{arcth}x arcthx arcth x = 1 2 ln 1 + x 1 − x \displaystyle \operatorname{arcth}x=\frac{1}{2}\ln\frac{1+x}{1-x} arcthx=21ln1−x1+x
三、微分方程
可分离变量的微分方程 [ 形如 : d y d x = f ( x ) ] [\mathbf{形如}: \displaystyle \frac{\text{d}y}{\text{d}x}=f(x)] [形如:dxdy=f(x)]
① After separating the variables,两端积分.
[② Determine the constants according to the definite solution conditions]
齐次方程 [ 形如 : d y d x = φ ( y x ) ] [\mathbf{形如}:\displaystyle \frac{\text{d}y}{\text{d}x}=φ(\frac{y}{x})] [形如:dxdy=φ(xy)],
看 x 、 y x、y x、y Whether the coefficient of degree is symmetric.
① 令 u = y x u = \dfrac{y}{x} u=xy, 则 y = u x y = ux y=ux, d y d x = u + x d u d x \displaystyle \frac{\text{d}y}{\text{d}x} = u + x\frac{\text{d}u}{\text{d}x} dxdy=u+xdxdu.
② 代入方程,分离变量 x x x 和 $u $后,两端积分.
③ 用 y x \dfrac{y}{x} xy代替 u u u .
[④ Determine the constants according to the definite solution conditions]
一阶线性微分方程 [ 形如: d y d x + P ( x ) ⋅ y = Q ( x ) ] [\mathbf{形如:} \dfrac{\text{d}y}{\text{d}x}+P(x)\cdot y=Q(x)] [形如:dxdy+P(x)⋅y=Q(x)]
(1) 当 Q ( x ) = 0 Q(x)=0 Q(x)=0 时,方程为『齐次』. (对应于 非齐次线性方程 的齐次线性方程 )
A general solution to a homogeneous linear equation: y = C e − ∫ P ( x ) d x \displaystyle y = Ce^{-\int P(x)\text{d}x} y=Ce−∫P(x)dx
(2) 当 Q ( x ) ≢ 0 Q(x)\not\equiv0 Q(x)≡0 时,方程为『非齐次』. (非齐次线性方程)
非A general solution to a homogeneous linear equation: y = e − ∫ P ( x ) d x ( ∫ Q ( x ) ⋅ e ∫ P ( x ) d x d x + C ) \displaystyle y = e^{-\int P(x)\text{d}x}(\int Q(x)\cdot e^{\int P(x)\text{d}x}\text{d}x+C) y=e−∫P(x)dx(∫Q(x)⋅e∫P(x)dxdx+C)
展开式: y = C e − ∫ P ( x ) d x + e − ∫ P ( x ) d x ∫ Q ( x ) ⋅ e ∫ P ( x ) d x d x \displaystyle y = Ce^{-\int P(x)\text{d}x} + e^{-\int P(x)\text{d}x}\int Q(x) \cdot e^{\int P(x)\text{d}x}\text{d}x y=Ce−∫P(x)dx+e−∫P(x)dx∫Q(x)⋅e∫P(x)dxdx
伯努利方程 [ 形如 : d y d x + P ( x ) ⋅ y = Q ( x ) ⋅ y n , ( n ≠ 0 , 1 ) ] [\mathbf{形如}:\dfrac{\text{d}y}{\text{d}x}+P(x)\cdot y= Q(x)\cdot y^n,\space(n\not=0,1)] [形如:dxdy+P(x)⋅y=Q(x)⋅yn, (n=0,1)]
① 两端同除以 y n y^n yn
② 设 z = y 1 − n z = y^{1-n} z=y1−n,则 d z d x = ( 1 − n ) y − n d y d x \displaystyle \frac{\text{d}z}{\text{d}x}=(1-n)y^{-n}\frac{\text{d}y}{\text{d}x} dxdz=(1−n)y−ndxdy
代入,得 1 1 − n ⋅ d z d x + P ( x ) z = Q ( x ) \dfrac{1}{1-n}\cdot \dfrac{\text{d}z}{\text{d}x} + P(x)z=Q(x) 1−n1⋅dxdz+P(x)z=Q(x)
d z d x + ( 1 − n ) P ( x ) z = ( 1 − n ) Q ( x ) \dfrac{\text{d}z}{\text{d}x}+(1-n)P(x)z = (1-n)Q(x) dxdz+(1−n)P(x)z=(1−n)Q(x)
③先求 z z z,再求 y y y.
可降阶的高阶微分方程
(1) [ 形如 : y ( n ) = f ( x ) ] [\mathbf{形如}:y^{(n)}=f(x)] [形如:y(n)=f(x)]
两端积分,得 y ( n − 1 ) = ∫ f ( x ) d x + C 1 \displaystyle y^{(n-1)}=\int f(x)\text{d}x+C_1 y(n−1)=∫f(x)dx+C1
Score until 得到通解 时.
(2) [ 形如 : y ′ ′ = f ( x , y ′ ) ] [\mathbf{形如}:y''= f(x,y')] [形如:y′′=f(x,y′)],没有 y
设 p = y ′ p = y' p=y′,则 y ′ ′ = p ′ y''=p' y′′=p′,
代入,得到 p ′ p' p′ 关于 p p p 和 x x x 的方程 p ′ = f ( x , p ) p'=f(x,p) p′=f(x,p)
(3) [ 形如 : y ′ ′ = f ( y , y ′ ) ] [\mathbf{形如}:y''=f(y,y')] [形如:y′′=f(y,y′)],没有 x
设 p = y ′ p = y' p=y′,则 y ′ ′ = d p d x = d p ⋅ d y d x ⋅ d y = p d p d y \displaystyle y'' = \frac{\text{d}p}{\text{d}x}=\frac{\text{d}p\space \cdot \space \text{d}y}{\text{d}x\space \cdot \space \text{d}y}=p\frac{\text{d}p}{\text{d}y} y′′=dxdp=dx ⋅ dydp ⋅ dy=pdydp
代入,得到 p d p d y = f ( y , p ) p\dfrac{\text{d}p}{\text{d}y} = f(y,p) pdydp=f(y,p)
Separation of variables to solve,之后把 p = y ′ p = y' p=y′ 代入,
[Find one of the constants based on known conditions,Continue to solve for separated variables.根据已知,Find the second constant]
线性相关 与 线性无关
- 定义:对于定义在区间 I I I 上的 n 个函数,Linear correlation is obtained if the following formula holds,否则无关.
k 1 y 1 + k 2 y 2 + ⋯ + k n y n ≡ 0 , ( ∀ x ∈ I ) ( k 1 , k 2 , ⋯ , k n 不全为 0 ) k_1 y_1+k_2 y_2 + \cdots + k_n y_n \equiv 0, (\forall x \in I )\space(k_1,k_2,\cdots,k_n不全为\space0) k1y1+k2y2+⋯+knyn≡0,(∀x∈I) (k1,k2,⋯,kn不全为 0)
二阶微分方程:A method to determine whether an equation is linear
若 y 1 ( x ) , y 2 ( x ) y_1(x),y_2(x) y1(x),y2(x)线性无关 ⇔ \Leftrightarrow ⇔ y 1 ( x ) y 2 ( x ) ≢ \dfrac{y_1(x)}{y_2(x)} \not\equiv y2(x)y1(x)≡ 常数.
- 高阶线性微分方程
二阶
[ 形如: d 2 y d x 2 + P ( x ) d y d x + Q ( x ) y = f ( x ) ] (6-1) \displaystyle [\mathbf{形如:} \frac{\text{d}^2y}{\text{d}x^2} + P(x)\frac{\text{d}y}{\text{d}x} +Q(x)y=f(x)]\tag{6-1} [形如:dx2d2y+P(x)dxdy+Q(x)y=f(x)](6-1)
① 齐次: f ( x ) ≡ 0 f(x) \equiv 0 f(x)≡0,设 ( 6 − 2 ) (6-2) (6−2) 是 ( 6 − 1 ) (6-1) (6−1) The corresponding homogeneous equation.
- 性质:homogeneous equationAdd any two solutions(或乘 C C C )的结果仍是solution of this homogeneous equation.
- 定理 1 :如果函数 y 1 ( x ) y_1(x) y1(x) 和 y 2 ( x ) y_2(x) y2(x) 是方程 ( 6 − 2 ) (6-2) (6−2) 的两个解,那么 函数 y = C 1 y 1 ( x ) + C 2 y 2 ( x ) y=C_1 y_1(x)+C_2 y_2(x) y=C1y1(x)+C2y2(x),也是方程 ( 6 − 2 ) (6-2) (6−2) 的解.
- 注意:函数 y = C 1 y 1 ( x ) + C 2 y 2 ( x ) y=C_1 y_1(x)+C_2 y_2(x) y=C1y1(x)+C2y2(x) Not necessarily an equation ( 6 − 2 ) (6-2) (6−2) 的通解.
- 定理 2 :如果 函数 y 1 ( x ) y_1(x) y1(x) 和 y 2 ( x ) y_2(x) y2(x) 是 线性无关 的特解,则函数 y = C 1 y 1 ( x ) + C 2 y 2 ( x ) y=C_1 y_1(x)+C_2 y_2(x) y=C1y1(x)+C2y2(x)是方程 ( 6 − 2 ) (6-2) (6−2) 的通解
② 非齐次: f ( x ) ≢ 0 f(x) \not\equiv 0 f(x)≡0
n 阶
[ 形如: y ( n ) + a 1 ( x ) y ( n − 1 ) + ⋯ + a n − 1 ( x ) y ′ + a n y = f ( x ) ] (6-n-1) \displaystyle [\mathbf{形如:} y^{(n)}+a_1(x)y^{(n-1)}+\cdots + a_{n-1}(x)y'+a_n y= f(x)]\tag{6-n-1} [形如:y(n)+a1(x)y(n−1)+⋯+an−1(x)y′+any=f(x)](6-n-1)
① 齐次:
如果 函数 y 1 ( x ) , y 2 ( x ) , ⋯ , y n ( x ) y_1(x),y_2(x),\cdots, y_n(x) y1(x),y2(x),⋯,yn(x) 是 线性无关 的特解,the functional equation ( 6 − n − 1 ) (6-n-1) (6−n−1) 的通解为:
y = C 1 y 1 ( x ) + C 2 y 2 ( x ) + ⋯ + C n y n ( x ) y=C_1 y_1(x)+C_2 y_2(x)+\cdots+C_n y_n(x) y=C1y1(x)+C2y2(x)+⋯+Cnyn(x)
边栏推荐
- 美团&上交开源PromptDet:无需标注,开放世界的目标检测器
- HJ3 obvious random number
- Flink CDC
- C专家编程 第8章 为什么程序员无法分清万圣节和圣诞节 8.2 根据位模式构筑图形
- Nature | 朱轩/陈福和/袁国勇等证实冠状病毒利用宿主半胱天冬酶-6 促进复制
- mysql连接WARN: Establishing SSL connection without server‘s identity verification is not recommended.
- dotnet 获取当前进程方法
- 微信自动发卡机器人说明
- 适配器模式:Swift 实现
- Solidigm officially launches PCIe 4.0 solid state drive Solidigm P41 Plus
猜你喜欢
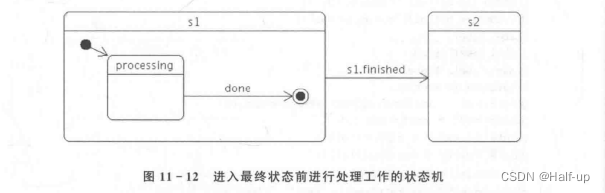
QT—状态机框架

多线程-同步问题
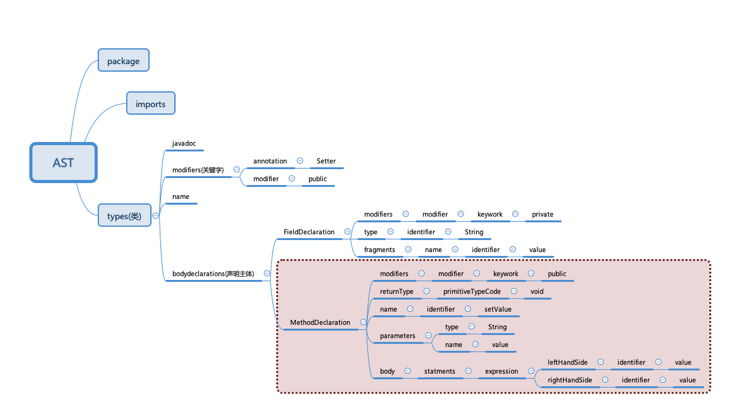
Introduction to common methods and principles of Lombok

MySQL: Calculate shortest distance between latitude and longitude using custom function

LeetCode 热题 HOT 100(10.删除链表的倒数第 N 个结点)

Lianshengde W801 series 2-WIFI one-key distribution network, information preservation
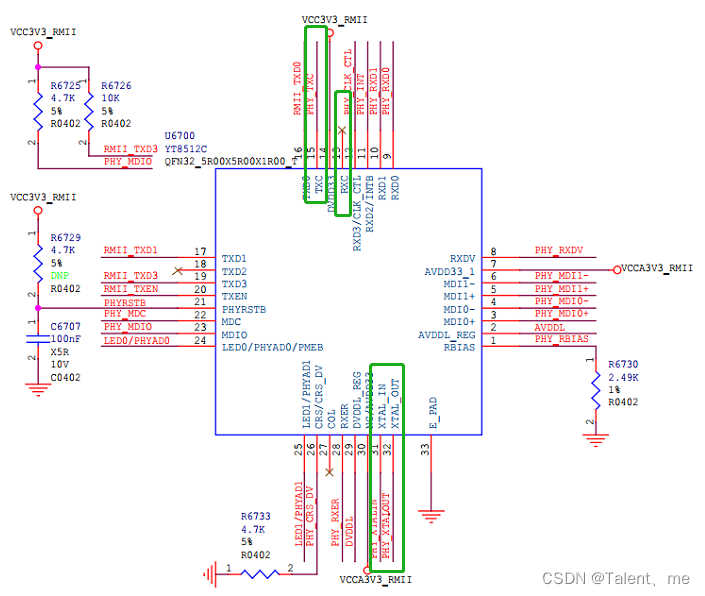
Based on RTL8201F Ethernet port 100M debugging notes in RK3566

【YOLOv7_0.1】网络结构与源码解析

深度之眼(二十一)——概率论

C Expert Programming Chapter 8 Why Programmers Can't Tell the Difference Between Halloween and Christmas 8.7 Implementing Finite State Machines in C
随机推荐
The ADC external RC circuit resistance and capacitance selection calculation method
X64 assembly language instruction encoding
AQS同步组件-Semaphore(信号量)解析和案例
HJ5 进制转换
go优先级队列实现
Programming Experts in C Chapter 8 Why Programmers Can't Tell the Difference Between Halloween and Christmas 8.9 How and Why Casting
dotnet 获取本机 IP 地址方法
dotnet 如何调试某个文件是哪个代码创建
C专家编程 第8章 为什么程序员无法分清万圣节和圣诞节 8.7 用C语言实现有限状态机
up to date!A summary of all Kaggle competition open source solutions and Top ideas, a total of 477 competitions!
How about Qiniu's CITIC Securities VIP commission account?Is it safe and reliable?
LeetCode 热题 HOT 100(10.删除链表的倒数第 N 个结点)
The solution to the view that the view is clipped and displayed incompletely in any inheritance hierarchy of SwiftUI
005_Ribbon负载均衡
LeetCode 热题 HOT 100(7.盛最多水的容器)
【PTA】L2-002 链表去重(25分)
联盛德W801系列2-WIFI一键配网,信息保存
Solidigm officially launches PCIe 4.0 solid state drive Solidigm P41 Plus
HJ2 计算某字符出现次数
C Expert Programming Chapter 7 Thinking About Memory 7.8 Take it easy --- "Thing King" and "Page Game"