当前位置:网站首页>最小圆覆盖(计算几何基础)
最小圆覆盖(计算几何基础)
2022-04-22 06:18:00 【S atur】


思路:
① 随机化点集(可降低复杂度)
② 初始随意找到两点,设为  和
和  ,以
,以  和
和  为直径做出初始圆
为直径做出初始圆  (以
(以 表示覆盖前 i 个点的最小圆)。
③ 依次加入新的点 ,若当前点
,若当前点  在圆
在圆  中,则
中,则  ,否则以
,否则以  作为新的直径端点做圆
作为新的直径端点做圆 (显然点
 在新圆的边界上)。
在新圆的边界上)。
④ 但是新圆 又不一定能包含之前的所有 i 个点,于是我们遍历找到前 i 个点中不在
中的点
 ,那么点
,那么点  和
和  一定都会在新圆的边界上,于是直接以
一定都会在新圆的边界上,于是直接以  为直径做出新圆
为直径做出新圆  。
。
⑤ 同样  也不一定能包含之前的所有 j 个点,于是再找到个点
也不一定能包含之前的所有 j 个点,于是再找到个点  , 确定点
, 确定点  ,
, ,
, 同在新圆的边界上,便可求得这三个点的外接圆即得到新圆
同在新圆的边界上,便可求得这三个点的外接圆即得到新圆  。
。
⑥ 由这三个循环不断更新迭代求出的圆即为覆盖当前所有点的最小圆。
⑦ 不知道为什么随机化会降低复杂度,这里引用大佬的证明:

其他具体的思路和证明参见其他大佬博客。
代码实现:
#include<bits/stdc++.h>
#define endl '\n'
#define null NULL
#define ll long long
#define int long long
#define pii pair<int, int>
#define lowbit(x) (x &(-x))
#define ls(x) x<<1
#define rs(x) (x<<1+1)
#define me(ar) memset(ar, 0, sizeof ar)
#define mem(ar,num) memset(ar, num, sizeof ar)
#define rp(i, n) for(int i = 0, i < n; i ++)
#define rep(i, a, n) for(int i = a; i <= n; i ++)
#define pre(i, n, a) for(int i = n; i >= a; i --)
#define IOS ios::sync_with_stdio(0); cin.tie(0);cout.tie(0);
const int way[4][2] = {
{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
using namespace std;
const int inf = 0x3f3f3f3f3f3f3f3f;
const double PI = acos(-1.0);
const double eps = 1e-6;
const ll mod = 1e9+7;
const int N = 2e5 + 5;
inline void read(int &x){
char t=getchar();
while(!isdigit(t)) t=getchar();
for(x=t^48,t=getchar();isdigit(t);t=getchar()) x=x*10+(t^48);
}
int n;
double r;
struct node{
double x, y;
}o, a[N];
double dis(node a, node b){ //得到两点之间的距离
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
void get(node a, node b, node c){ //三点确定一圆
double x1 = a.x-b.x, y1 = a.y-b.y;
double d1 = (a.x*a.x-b.x*b.x+a.y*a.y-b.y*b.y)/2;
double x2 = a.x-c.x, y2 = a.y-c.y;
double d2 = (a.x*a.x-c.x*c.x+a.y*a.y-c.y*c.y)/2;
o.x = (d1*y2-y1*d2)/(x1*y2-y1*x2);
o.y = (d2*x1-x2*d1)/(x1*y2-y1*x2);
r = dis(o, a);
}
signed main()
{
IOS;
cin >> n;
for(int i = 1; i <= n; i ++)
cin >> a[i].x >> a[i].y;
random_shuffle(a+1, a+n+1);
o = a[1]; //先以第一个点为圆心
for(int i = 2; i <= n; i ++){
if(dis(o, a[i])>r+eps){ //找到第一个不在圆内的点
o = {(a[1].x+a[i].x)/2, (a[1].y+a[i].y)/2}; //更新圆心
r = dis(o, a[i]); //更新半径
for(int j = 1; j < i; j ++){
if(dis(o, a[j])>r+eps){ //找到第二个不在圆内的点
o = {(a[i].x+a[j].x)/2, (a[i].y+a[j].y)/2}; //更新圆心
r = dis(o, a[j]); //更新半径
for(int k = 1; k <j; k ++){
if(dis(o, a[k])>r+eps){ //找到第三个不在圆内的点
get(a[i], a[j], a[k]); //圆外的三个点来更新最小圆
}
}
}
}
}
}
printf("%.10f\n%.10f %.10f\n", r, o.x, o.y);
return 0;
}
版权声明
本文为[S atur]所创,转载请带上原文链接,感谢
https://blog.csdn.net/Satur9/article/details/115878134
边栏推荐
猜你喜欢

详解冒泡序列与数组名

LeetCode - 6 - (字符串相乘、下一個更大元素<ⅠⅡⅢ>、k個一組翻轉鏈錶)

字节暑期实习一面——20220304
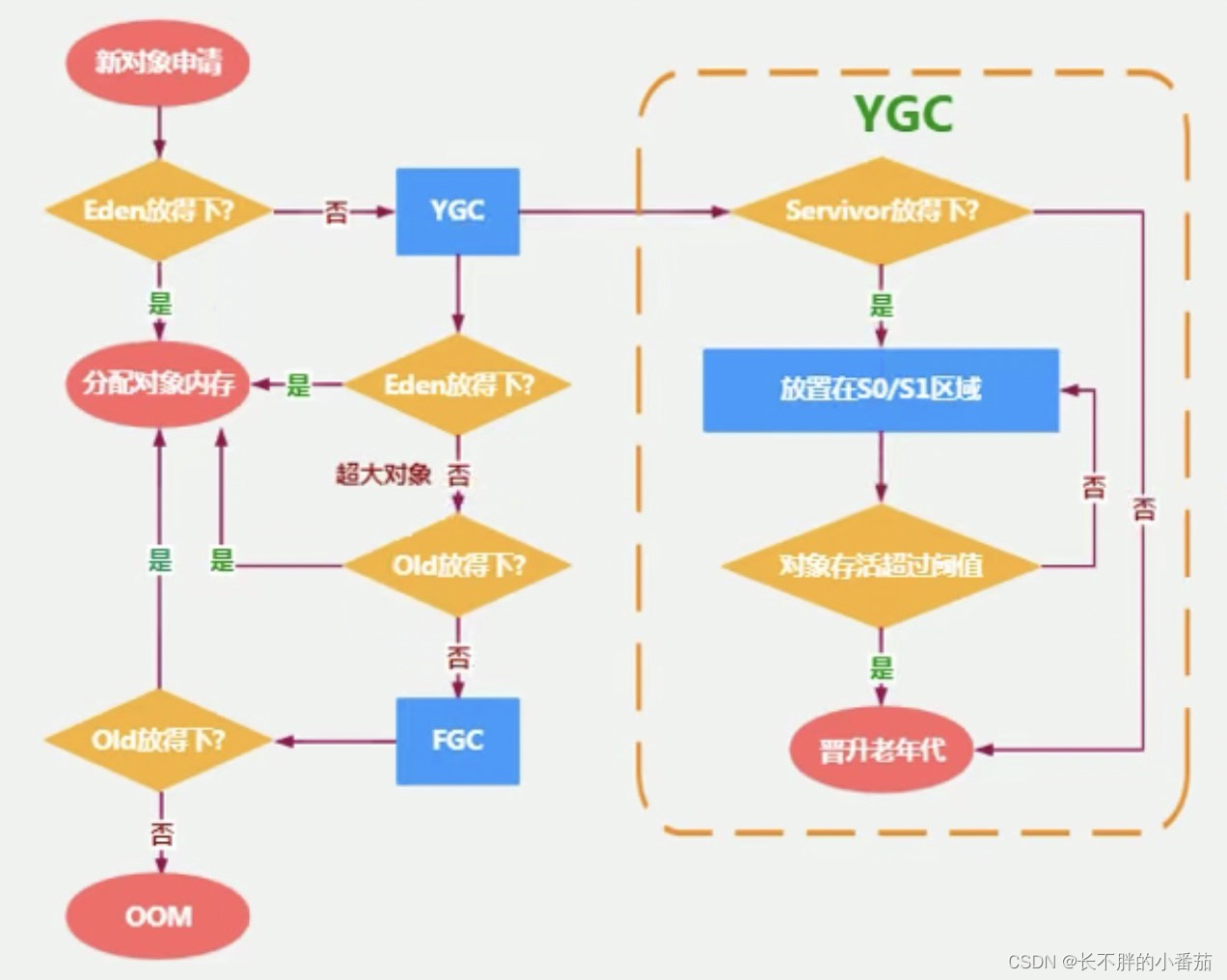
Interviewers often ask about the general process and special circumstances of object allocation

C language | pointer

LeetCode - 8 - (三数之和、Z字形变换、两数之和<链表>、盛最多水的容器、电话号码的字母组合)
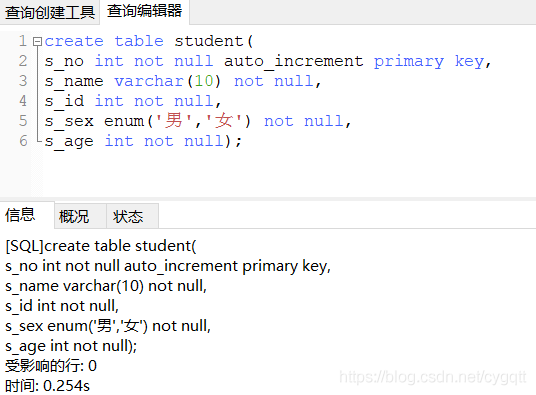
Complete a student information management system and systematically practice object-oriented, function, string and other knowledge. Realize the comprehensive application of knowledge. Use classes, fun
浅谈时间复杂度与空间复杂度

L1-064 估值一亿的AI核心代码 (20 分) 格式错误

When latex uses the template, the caption title of the picture cannot be left aligned
随机推荐
【数论】【不定方程】n元一次不定方程、佩尔方程、毕达哥拉斯定理、费马大定理
Educational Codeforces Round 122 (Rated for Div. 2)
CodeTON Round 1 (Div. 1 + Div. 2, Rated, Prizes)
链表难题记录一
[number theory] prime number (4): decomposition of numbers (Pollard rho)
14 lines of code to complete arbitrary selection of image crawling
In the process of class loading, the allocation area of class variables is different from that of instance variables
L2-004 这是二叉搜索树吗?(先序输入&判断搜索二叉树&后序输出)
小游戏——三子棋
Add author photos and author profiles to latex
Codeforces Round #623
Detailed tree array template -- Theory and code implementation
Interviewers often ask about the general process and special circumstances of object allocation
面试官常问的,对象分配的一般过程及特殊情况
牛客xb月赛45题解
最强数组学习之路
323 · 字符串游戏
字节暑期实习一面——20220304
详解冒泡序列与数组名
队列(详解)——手撕队列习题