链式二叉树

我们需要明白一点，就是普通的二叉树==增删查改==没有什么价值，因为普通二叉树用来存数据复杂且不方便

那么链式二叉树有什么好的地方呢

==价值体现：==在他的基础之上，增加一些性质，才有意义

1.==搜索二叉树 ：==最多查找高度次—>时间复杂度O(N)—>单链树也就引出平衡二叉树—>AVL树和红黑树

2.Huffman 树（以后再说，反正不是现在了解的）

我们不关注普通二叉树的增删查改，我们关注递归遍历结构

1.为后面学习更有用树打基础

2.很多oj题结构普遍二叉树

==二叉树被分成 根 左子树 右子树==

二叉树的遍历

前序、中序以及后序遍历

学习二叉树结构，最简单的方式就是遍历。所谓==二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。==访问结点所做的操作依赖于具体的应用问题。遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

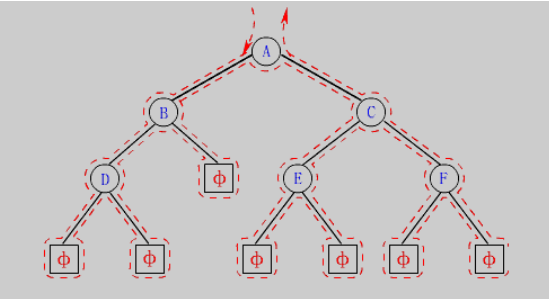
按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：（上图为例图）（前中后访问根的时机不一样）

1.前序遍历(Preorder Traversal 亦称==先序遍历==)——访问根结点的操作发生在遍历其左右子树之前。==根 左子树 右子树==

上图前序遍历的顺序是：A B D NULL NULL NULL C E NULL NULL F NULL NULL==只有把空放进去才能真正的知道思想，那些不加 空的就是耍流氓，没错说的就是你们老师，对你们耍流氓==

2.中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。==左子树 根 右子树==

上图中序遍历的顺序是：NULL D NULL B NULL A （这时候想访问C就得访问E）NULL E NULL C NULL F NULL

3.后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。==左子树 右子树 根==

上图后序遍历的顺序是：NULL NULL D NULL B NULL NULL E NULL NULL F C A

分治

这里我们用的思想是分治的思想，分而治之-----大事化小，小事化了

二叉树

二叉树节点

//二叉树数据类型typedef char BTDataType;//二叉树节点typedef struct BinaryTreeNode{	struct BinaryTreeNode* left;	struct BinaryTreeNode* right;	BTDataType data;}BTNode;

我们把上面的树建好

//创建树 我们不学二叉树的增删查改原因就在这，我们想要啥树自己链一个就行，没必要增删查改BTNode* CreatBinaryTree(){	BTNode* nodeA = BuyNode('A');	BTNode* nodeB = BuyNode('B');	BTNode* nodeC = BuyNode('C');	BTNode* nodeD = BuyNode('D');	BTNode* nodeE = BuyNode('E');	BTNode* nodeF = BuyNode('F');	nodeA->left = nodeB;	nodeA->right = nodeC;	nodeB->left = nodeD;	nodeC->left = nodeE;	nodeC->right = nodeF;	return nodeA;}

二叉树前序遍历

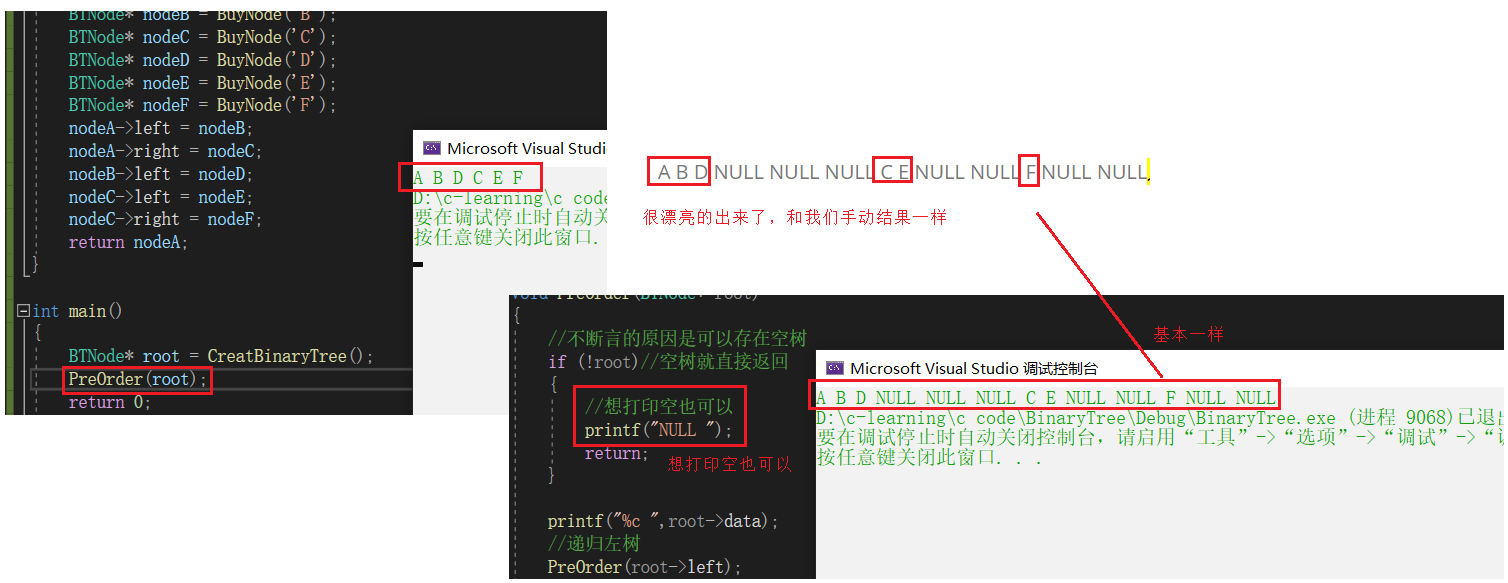
==这张图我实际上是想通过左右与上下滚动联合操作来截图的，然后我就找几个小时，基本能找的都找了，全网没有左右滚动截图的软件基本全是截图后窗口亮，不可以操作外面的滚动条，就算能操作也不可以左右滚动截图==

//二叉树前序遍历void PreOrder(BTNode* root){	//不断言的原因是可以存在空树	if (!root)//空树就直接返回	{		return;	}	printf("%c ",root->data);	//递归左树	PreOrder(root->left);	//递归右树	PreOrder(root->right);}

二叉树中序遍历

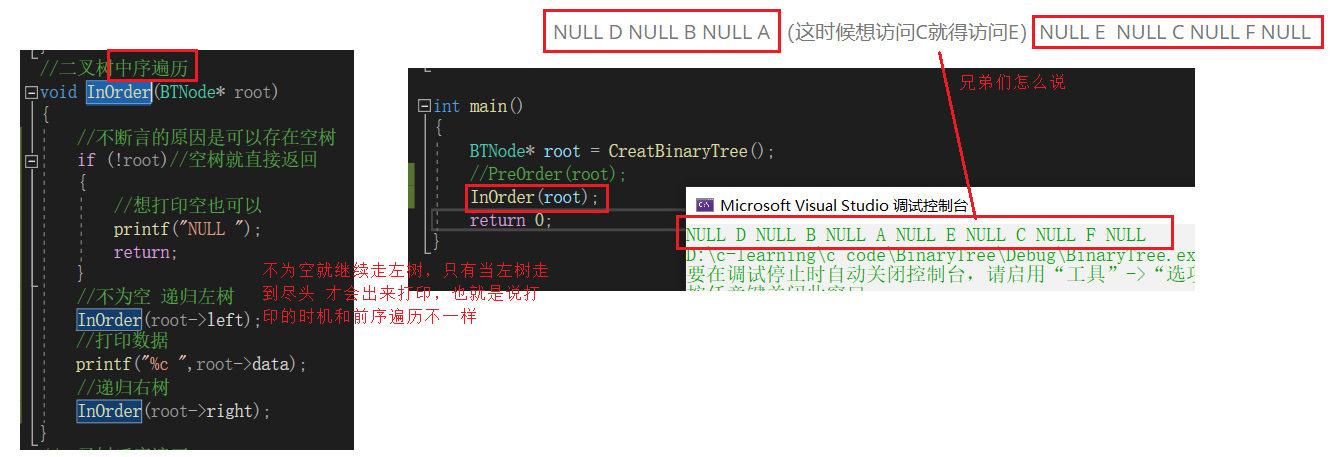
==我故意写成一个窗口的宽度，不然会很麻烦==

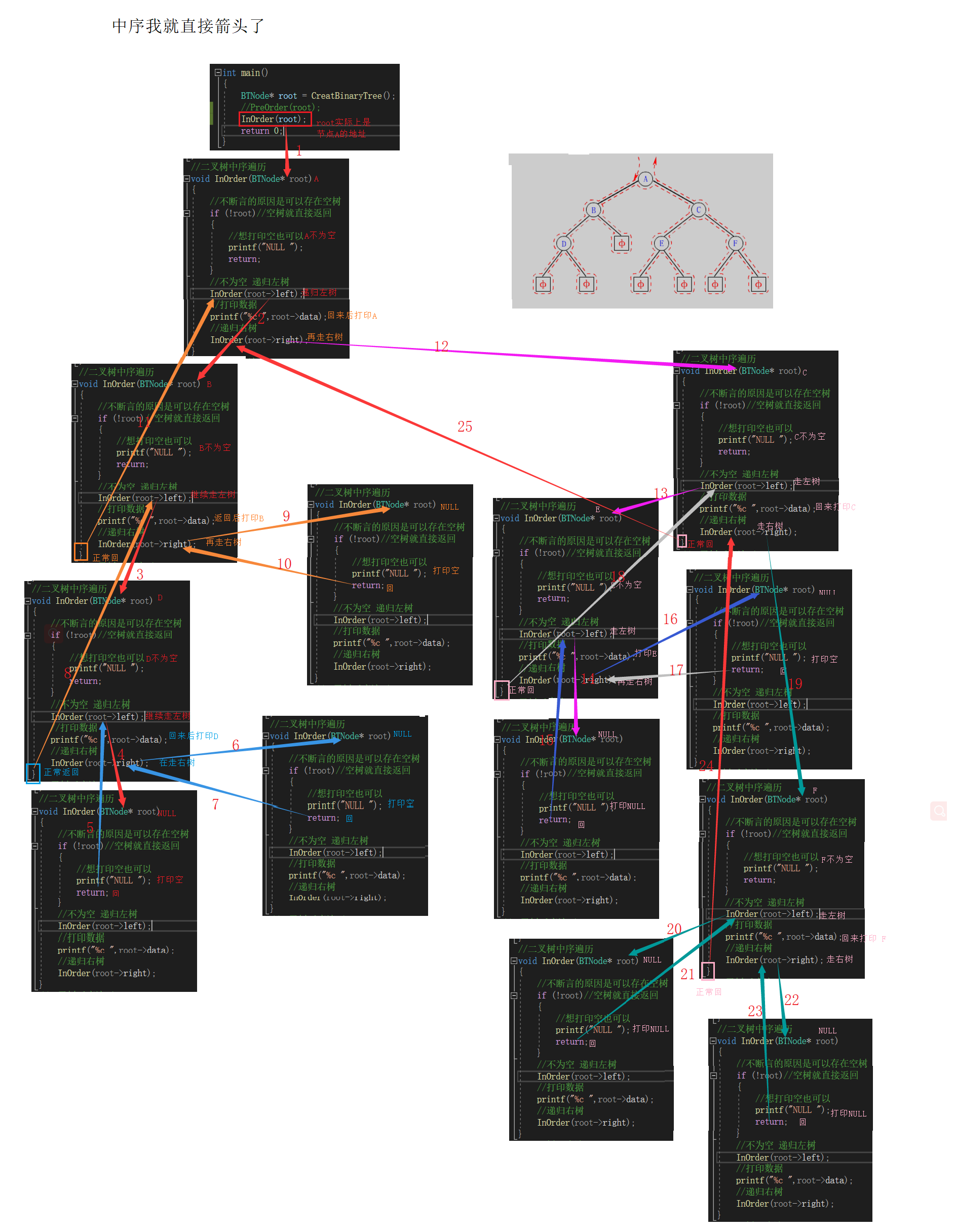
//二叉树中序遍历void InOrder(BTNode* root){	//不断言的原因是可以存在空树	if (!root)//空树就直接返回	{		//想打印空也可以		printf("NULL ");		return;	}	//不为空 递归左树	InOrder(root->left);	//打印数据	printf("%c ",root->data);	//递归右树	InOrder(root->right);}

二叉树后序遍历

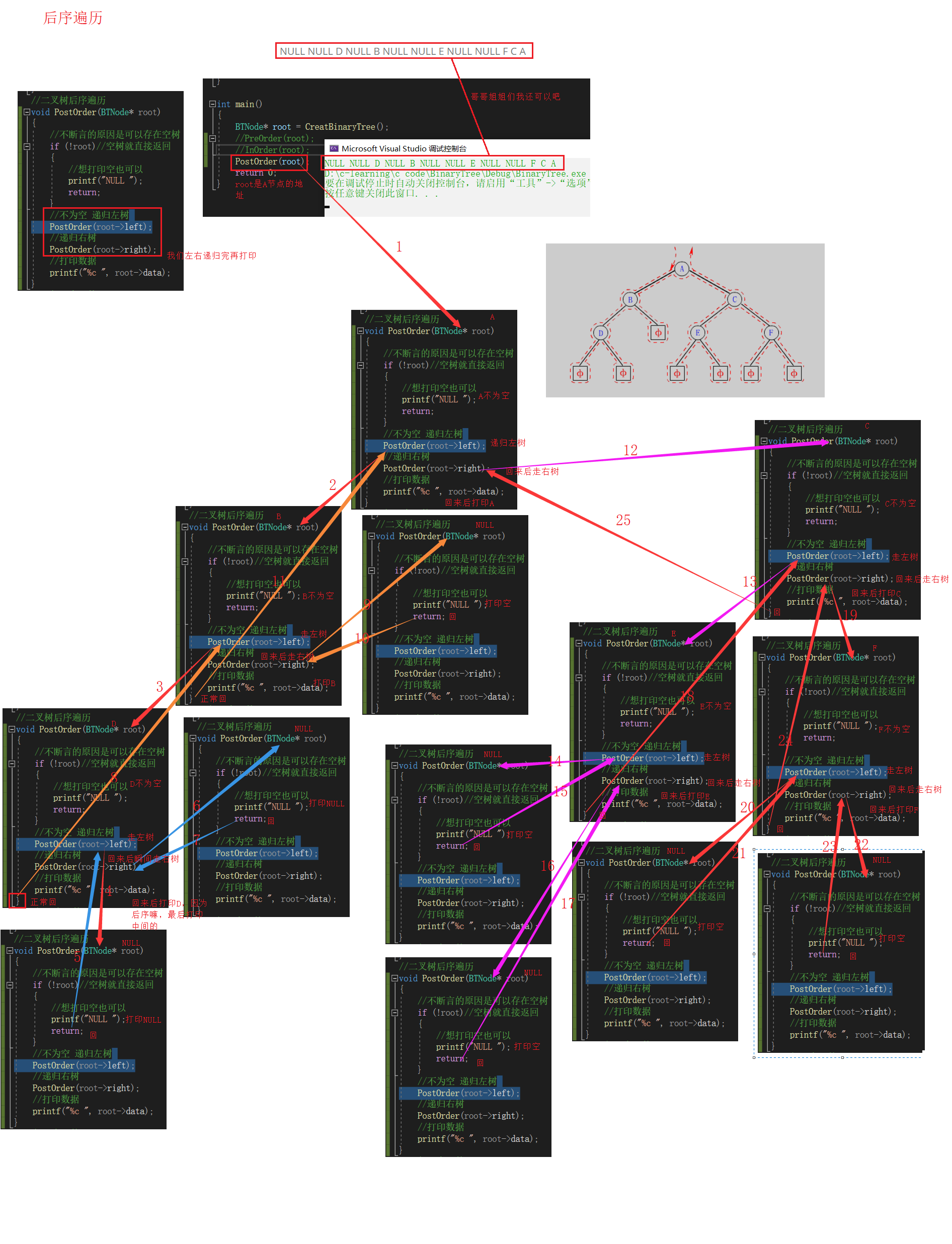
//二叉树后序遍历void PostOrder(BTNode* root){	//不断言的原因是可以存在空树	if (!root)//空树就直接返回	{		//想打印空也可以		printf("NULL ");		return;	}	//不为空 递归左树	PostOrder(root->left);	//递归右树	PostOrder(root->right);	//打印数据	printf("%c ", root->data);}

二叉树节点个数

次数用传址的方式

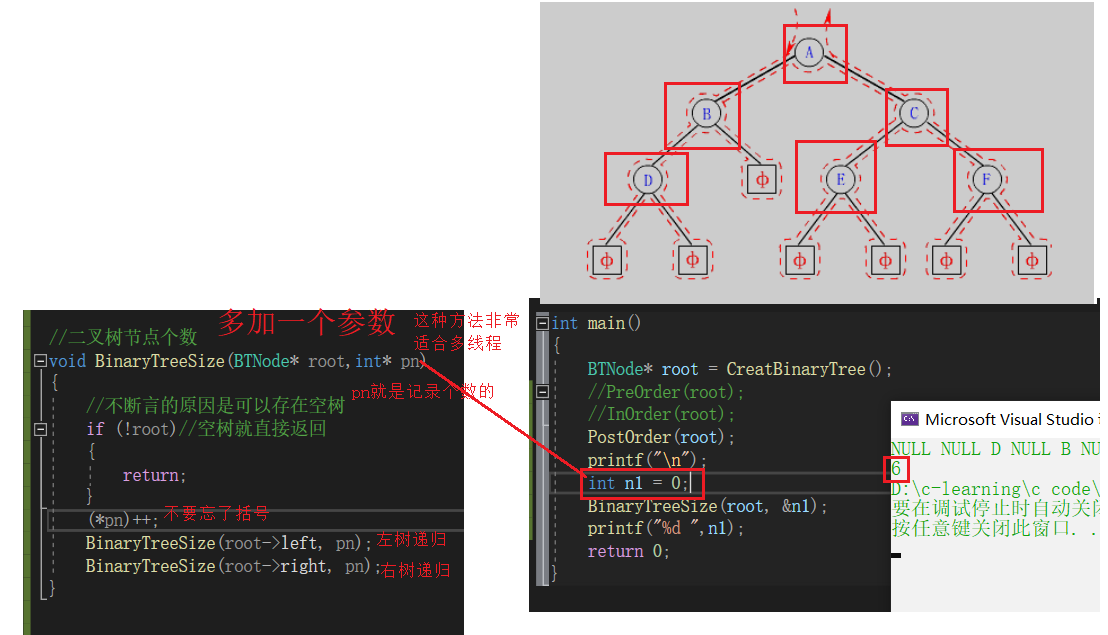
//二叉树节点个数void BinaryTreeSize(BTNode* root,int* pn){	//不断言的原因是可以存在空树	if (!root)//空树就直接返回	{		return;	}	(*pn)++;	BinaryTreeSize(root->left, pn);	BinaryTreeSize(root->right, pn);}

次数用返回值的方式（假如我是代码我必然要嫁给这条代码）

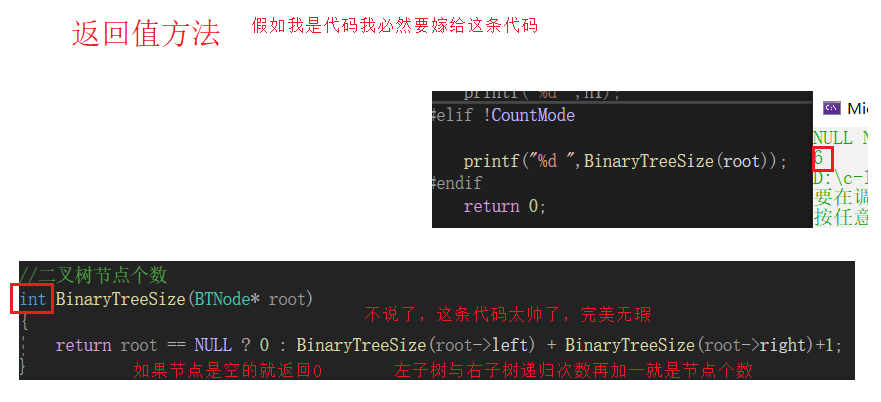
//二叉树节点个数int BinaryTreeSize(BTNode* root){	return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right)+1;}

二叉树叶子节点个数

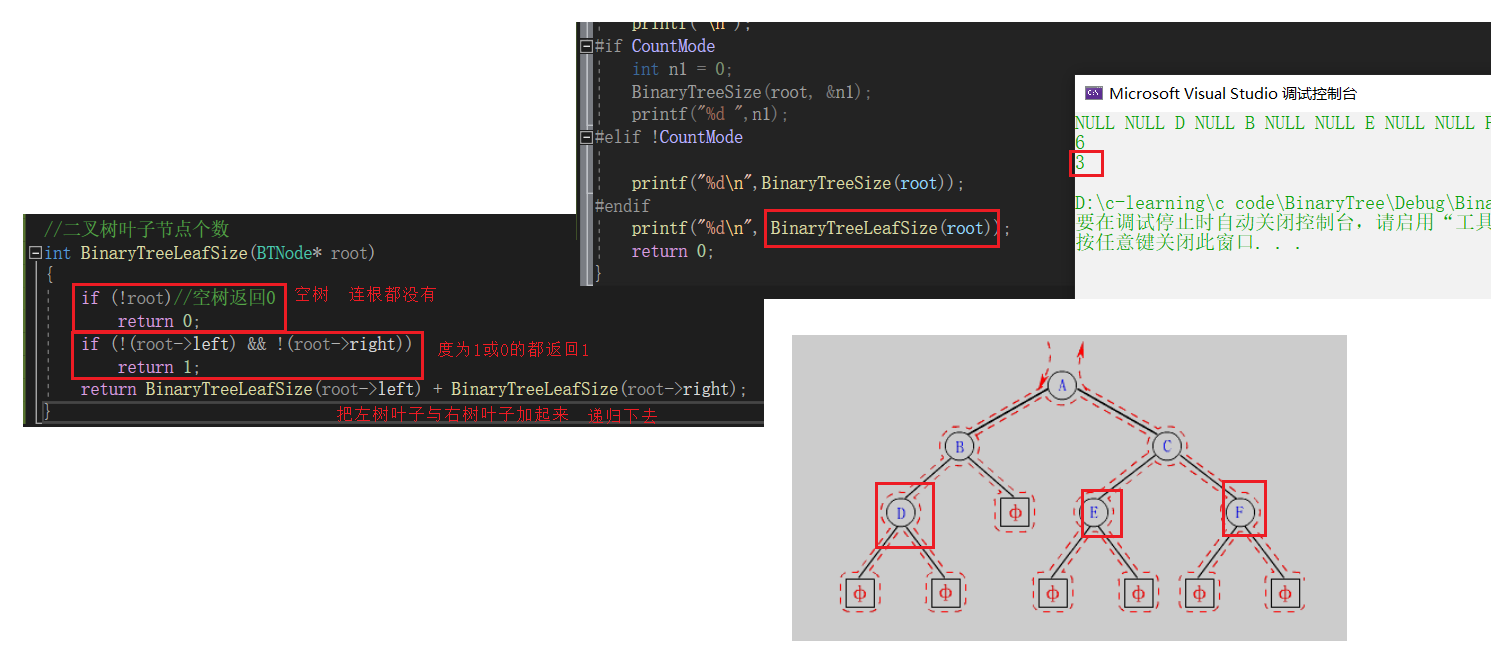
//二叉树叶子节点个数int BinaryTreeLeafSize(BTNode* root){	if (!root)//空树返回0		return 0;	if (!(root->left) && !(root->right))		return 1;	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);}

二叉树第k层节点个数

//二叉树第k层节点个数int BinaryTreeLevelSize(BTNode* root, int k){	if (!root)		return 0;	if (1 == k)		return 1;	//root不等于空，k也不等于1，说明root这棵树的第k层节点在子树里面	//转换成求左右子树的第k-1层节点数量	return BinaryTreeLevelSize(root->left, k - 1) + BinaryTreeLevelSize(root->right, k - 1);}

二叉树深度/高度

//二叉树深度/高度int BinaryTreeDepth(BTNode* root){	if (!root)		return 0;	//把递归的数用变量保存起来，减少资源的消耗	int leftDepth = BinaryTreeDepth(root->left);	int rightDepth = BinaryTreeDepth(root->right);	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;}

二叉树查找值为x的节点

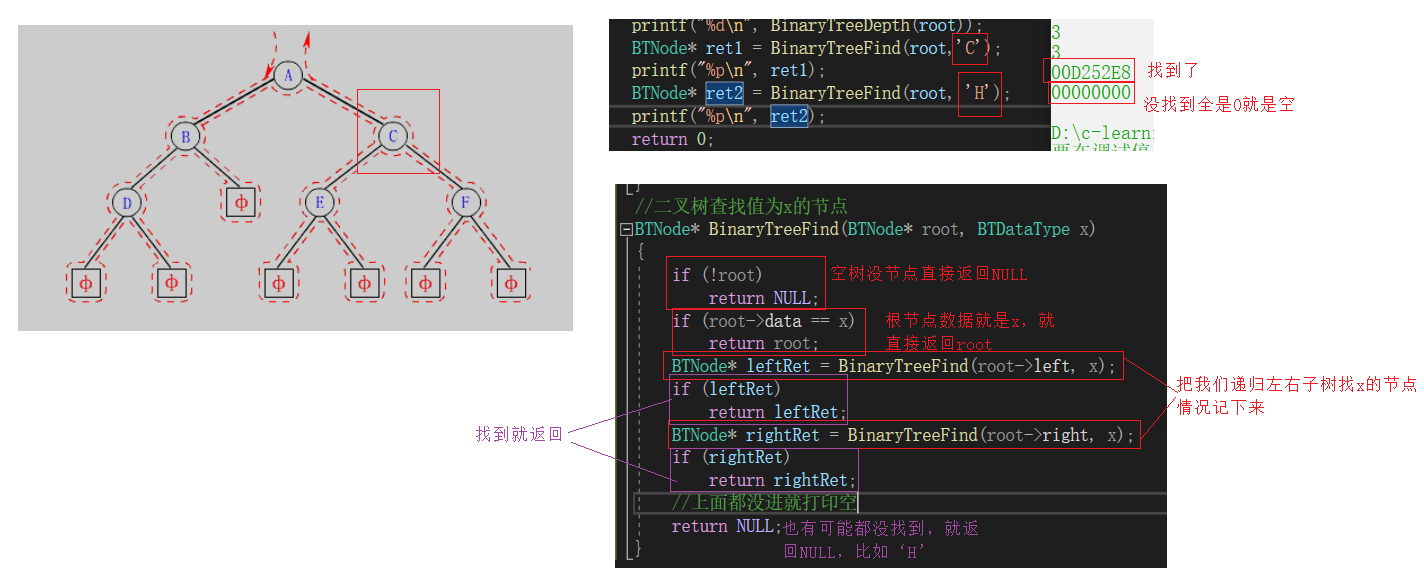
//二叉树查找值为x的节点BTNode* BinaryTreeFind(BTNode* root, BTDataType x){	if (!root)		return NULL;	if (root->data == x)		return root;	BTNode* leftRet = BinaryTreeFind(root->left, x);	if (leftRet)		return leftRet;	BTNode* rightRet = BinaryTreeFind(root->right, x);	if (rightRet)		return rightRet;	//上面都没进就打印空	return NULL;}

二叉树层序遍历

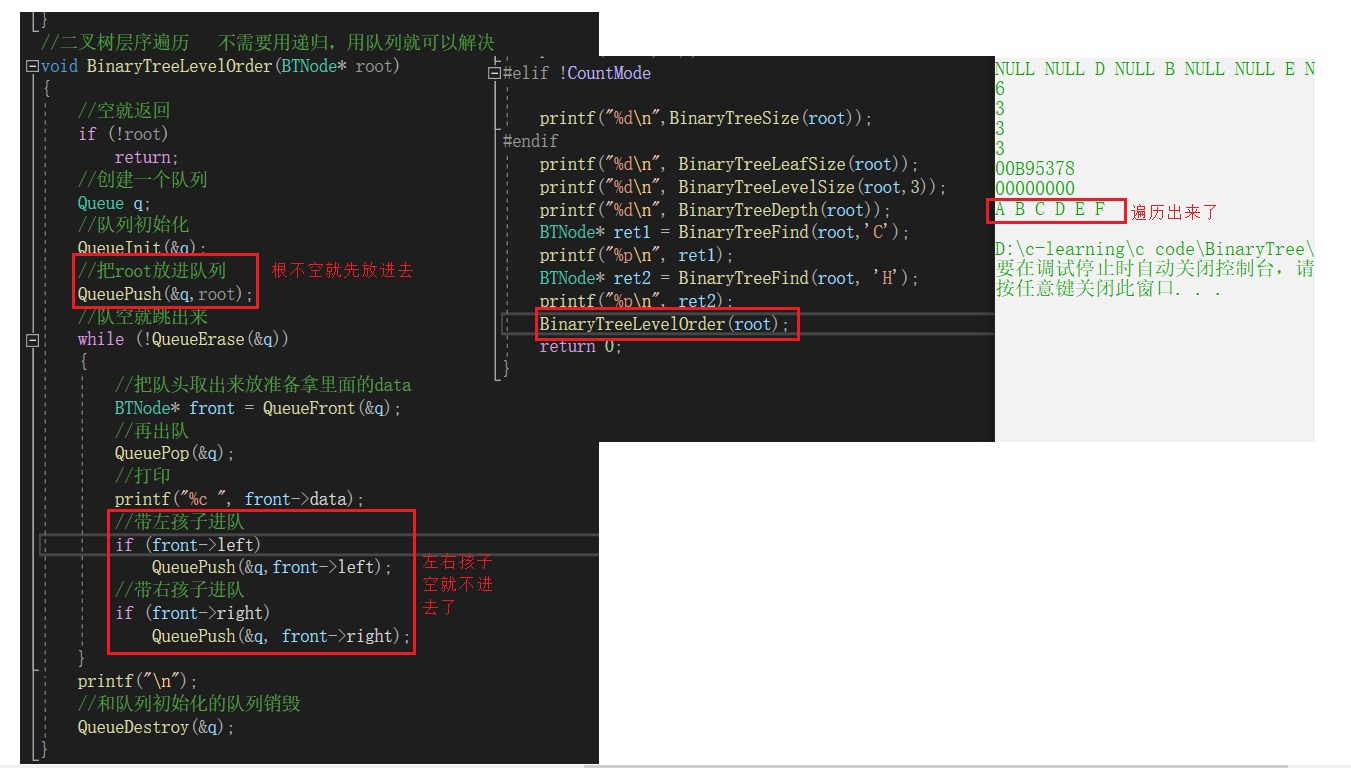
//二叉树层序遍历 不需要用递归，用队列就可以解决void BinaryTreeLevelOrder(BTNode* root){	//空就返回	if (!root)		return;	//创建一个队列	Queue q;	//队列初始化	QueueInit(&q);	//把root放进队列	QueuePush(&q,root);	//队空就跳出来	while (!QueueErase(&q))	{		//把队头取出来放准备拿里面的data		BTNode* front = QueueFront(&q);		//再出队		QueuePop(&q);		//打印		printf("%c ", front->data);		//带左孩子进队		if (front->left)			QueuePush(&q,front->left);		//带右孩子进队		if (front->right)			QueuePush(&q, front->right);	}	printf("\n");	//和队列初始化的队列销毁	QueueDestroy(&q);}

判断二叉树是否是完全二叉树BinaryTreeComplete

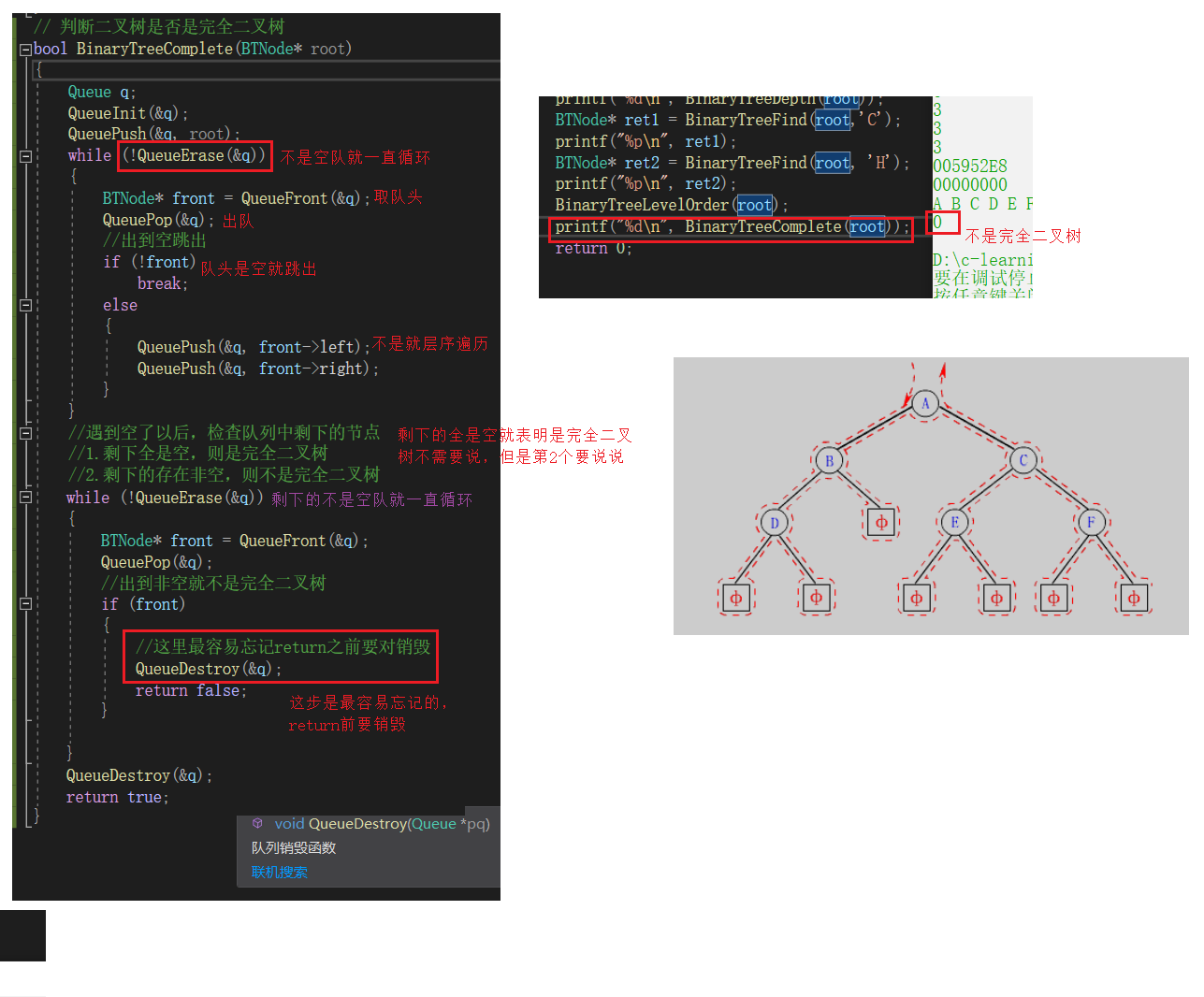
// 判断二叉树是否是完全二叉树bool BinaryTreeComplete(BTNode* root){	Queue q;	QueueInit(&q);	QueuePush(&q, root);	while (!QueueErase(&q))	{		BTNode* front = QueueFront(&q);		QueuePop(&q);		//出到空跳出		if (!front)			break;		else		{			QueuePush(&q, front->left);			QueuePush(&q, front->right);		}	}	//遇到空了以后，检查队列中剩下的节点	//1.剩下全是空，则是完全二叉树	//2.剩下的存在非空，则不是完全二叉树	while (!QueueErase(&q))	{		BTNode* front = QueueFront(&q);		QueuePop(&q);		//出到非空就不是完全二叉树		if (front)		{			//这里最容易忘记return之前要对销毁			QueueDestroy(&q);			return false;		}			}	QueueDestroy(&q);	return true;}

二叉树销毁BinaryTreeDestory

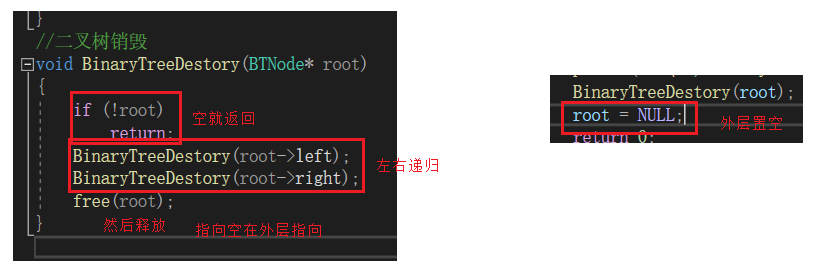
//二叉树销毁void BinaryTreeDestory(BTNode* root){	if (!root)		return;	BinaryTreeDestory(root->left);	BinaryTreeDestory(root->right);	free(root);}

代码

BinaryTree.h

#pragma once#include <stdio.h>#include <stdlib.h>#include <assert.h>#include <stdbool.h>#define CountMode 0//二叉树数据类型typedef char BTDataType;//二叉树节点typedef struct BinaryTreeNode{	struct BinaryTreeNode* left;	struct BinaryTreeNode* right;	BTDataType data;}BTNode;//二叉树前序遍历extern void PreOrder(BTNode* root);//二叉树中序遍历extern void InOrder(BTNode* root);//二叉树后序遍历extern void PostOrder(BTNode* root);//获得节点函数extern BTNode* BuyNode(BTDataType x);#if CountMode//二叉树节点个数extern void BinaryTreeSize(BTNode* root, int* pn);#elif !CountMode//二叉树节点个数extern int BinaryTreeSize(BTNode* root);#endif//二叉树叶子节点个数extern int BinaryTreeLeafSize(BTNode* root);//二叉树第k层节点个数extern int BinaryTreeLevelSize(BTNode* root,int k);//二叉树深度/高度extern int BinaryTreeDepth(BTNode* root);//二叉树查找值为x的节点extern BTNode* BinaryTreeFind(BTNode* root, BTDataType x);//二叉树层序遍历 extern void BinaryTreeLevelOrder(BTNode* root);// 判断二叉树是否是完全二叉树extern bool BinaryTreeComplete(BTNode* root);//二叉树销毁extern void BinaryTreeDestory(BTNode* root);

BinaryTree.c

#define _CRT_SECURE_NO_WARNINGS 1#include"BinaryTree.h"#include"Queue.h"//获得节点函数BTNode* BuyNode(BTDataType x){	//创建二叉树节点	BTNode* node = (BTNode*)malloc(sizeof(BTNode));	//检查是否成功创建	assert(node);	//把数据放到节点里	node->data = x;	//左右子树先空树	node->left = node->right = NULL;	return node;}//二叉树前序遍历void PreOrder(BTNode* root){	//不断言的原因是可以存在空树	if (!root)//空树就直接返回	{		//想打印空也可以		printf("NULL ");		return;	}	printf("%c ",root->data);	//递归左树	PreOrder(root->left);	//递归右树	PreOrder(root->right);}//二叉树中序遍历void InOrder(BTNode* root){	//不断言的原因是可以存在空树	if (!root)//空树就直接返回	{		//想打印空也可以		printf("NULL ");		return;	}	//不为空 递归左树	InOrder(root->left);	//打印数据	printf("%c ",root->data);	//递归右树	InOrder(root->right);}//二叉树后序遍历void PostOrder(BTNode* root){	//不断言的原因是可以存在空树	if (!root)//空树就直接返回	{		//想打印空也可以		printf("NULL ");		return;	}	//不为空 递归左树	PostOrder(root->left);	//递归右树	PostOrder(root->right);	//打印数据	printf("%c ", root->data);}#if CountMode//二叉树节点个数void BinaryTreeSize(BTNode* root,int* pn){	//不断言的原因是可以存在空树	if (!root)//空树就直接返回	{		return;	}	(*pn)++;	BinaryTreeSize(root->left, pn);	BinaryTreeSize(root->right, pn);}#elif !CountMode//二叉树节点个数int BinaryTreeSize(BTNode* root){	return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right)+1;}#endif//二叉树叶子节点个数int BinaryTreeLeafSize(BTNode* root){	if (!root)//空树返回0		return 0;	if (!(root->left) && !(root->right))		return 1;	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);}//二叉树第k层节点个数int BinaryTreeLevelSize(BTNode* root, int k){	//k小于等于零直接断言 因为都是从第一层开始的	assert(k > 0);	if (!root)		return 0;	if (1 == k)		return 1;	//root不等于空，k也不等于1，说明root这棵树的第k层节点在子树里面	//转换成求左右子树的第k-1层节点数量	return BinaryTreeLevelSize(root->left, k - 1) + BinaryTreeLevelSize(root->right, k - 1);}//二叉树深度/高度int BinaryTreeDepth(BTNode* root){	if (!root)		return 0;	//把递归的数用变量保存起来，减少资源的消耗	int leftDepth = BinaryTreeDepth(root->left);	int rightDepth = BinaryTreeDepth(root->right);	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;}//二叉树查找值为x的节点BTNode* BinaryTreeFind(BTNode* root, BTDataType x){	if (!root)		return NULL;	if (root->data == x)		return root;	BTNode* leftRet = BinaryTreeFind(root->left, x);	if (leftRet)		return leftRet;	BTNode* rightRet = BinaryTreeFind(root->right, x);	if (rightRet)		return rightRet;	//上面都没进就打印空	return NULL;}//二叉树层序遍历 不需要用递归，用队列就可以解决void BinaryTreeLevelOrder(BTNode* root){	//空就返回	if (!root)		return;	//创建一个队列	Queue q;	//队列初始化	QueueInit(&q);	//把root放进队列	QueuePush(&q,root);	//队空就跳出来	while (!QueueErase(&q))	{		//把队头取出来放准备拿里面的data		BTNode* front = QueueFront(&q);		//再出队		QueuePop(&q);		//打印		printf("%c ", front->data);		//带左孩子进队		if (front->left)			QueuePush(&q,front->left);		//带右孩子进队		if (front->right)			QueuePush(&q, front->right);	}	printf("\n");	//和队列初始化的队列销毁	QueueDestroy(&q);}// 判断二叉树是否是完全二叉树bool BinaryTreeComplete(BTNode* root){	Queue q;	QueueInit(&q);	QueuePush(&q, root);	while (!QueueErase(&q))	{		BTNode* front = QueueFront(&q);		QueuePop(&q);		//出到空跳出		if (!front)			break;		else		{			QueuePush(&q, front->left);			QueuePush(&q, front->right);		}	}	//遇到空了以后，检查队列中剩下的节点	//1.剩下全是空，则是完全二叉树	//2.剩下的存在非空，则不是完全二叉树	while (!QueueErase(&q))	{		BTNode* front = QueueFront(&q);		QueuePop(&q);		//出到非空就不是完全二叉树		if (front)		{			//这里最容易忘记return之前要对销毁			QueueDestroy(&q);			return false;		}			}	QueueDestroy(&q);	return true;}//二叉树销毁void BinaryTreeDestory(BTNode* root){	if (!root)		return;	BinaryTreeDestory(root->left);	BinaryTreeDestory(root->right);	free(root);}

test.c

#define _CRT_SECURE_NO_WARNINGS 1#include"BinaryTree.h"#include"Queue.h"//创建树 我们不学二叉树的增删查改原因就在这，我们想要啥树自己链一个就行，没必要增删查改BTNode* CreatBinaryTree(){	BTNode* nodeA = BuyNode('A');	BTNode* nodeB = BuyNode('B');	BTNode* nodeC = BuyNode('C');	BTNode* nodeD = BuyNode('D');	BTNode* nodeE = BuyNode('E');	BTNode* nodeF = BuyNode('F');	nodeA->left = nodeB;	nodeA->right = nodeC;	nodeB->left = nodeD;	nodeC->left = nodeE;	nodeC->right = nodeF;	return nodeA;}int main(){	BTNode* root = CreatBinaryTree();	//PreOrder(root);	//InOrder(root);	PostOrder(root);	printf("\n");#if CountMode	int n1 = 0;	BinaryTreeSize(root, &n1);	printf("%d ",n1);#elif !CountMode	printf("%d\n",BinaryTreeSize(root));#endif	printf("%d\n", BinaryTreeLeafSize(root));	printf("%d\n", BinaryTreeLevelSize(root,3));	printf("%d\n", BinaryTreeDepth(root));	BTNode* ret1 = BinaryTreeFind(root,'C');	printf("%p\n", ret1);	BTNode* ret2 = BinaryTreeFind(root, 'H');	printf("%p\n", ret2);	BinaryTreeLevelOrder(root);	printf("%d\n", BinaryTreeComplete(root));	BinaryTreeDestory(root);	root = NULL;	return 0;}