当前位置:网站首页>leetcode:296.最佳的碰头地点
leetcode:296.最佳的碰头地点
2022-08-08 16:40:00 【OceanStar的学习笔记】
题目来源
题目描述

题目解析
思路一
先看一维是由两个点A和B的情况:
A_____P_______B_
可以发现,只要开会位置P在[A,B]区间内,不管在哪,距离之和都是A和B之间的距离。如果P不在[A,B]区间内,那么距离之和就会大于A和B之间的距离
现在再加两个点C和D:
C_____A_____P_______B______D
通过分析可以得出,P点的最佳位置就是在 [A, B] 区间内,这样和四个点的距离之和为AB距离加上 CD 距离,在其他任意一点的距离都会大于这个距离
因此,只要给位置排好序,然后用最后一个坐标减去第一个坐标,即 CD 距离,倒数第二个坐标减去第二个坐标,即 AB 距离,以此类推,直到最中间停止,那么一维的情况分析出来了
二维的情况就是两个一维相加即可
思路二
根据计算距离的公式可以看出,一个点的横坐标和纵坐标计算是相互独立的。
因此我们可以把二维问题拆成一维问题。
假设一个一维数组如下:

我们要找出一个点,使得所有的 1 到该点的距离之和最小。
其实我们一眼可以看出,这个最优碰头点是索引 6 的地方。
那为什么索引 6 就是最优的碰头点呢?我们下面来逐一分析:
首先,无论碰头点在何处,索引 0 和索引 9 到达这个碰头点走的距离之和肯定是 9.

如果碰头点在索引 6 的左侧,那么索引 5、6、8 到碰头点的距离之和肯定大于 8-5:

如果碰头点在所有 6 的右侧,那么索引 5、6、8 到碰头点的距离之和肯定大于 8-5;

因此,位置 6 就是最优碰头点。
这个位置的索引恰好是所有 1 所在索引的中位数。
比如上面的 1 所在索引分别是 {0,5,6,8,9} ,中位数为 6。
由于题目是二维问题,且距离计算时,横纵坐标的计算是相互独立的,因此把问题拆分成两个一维问题之和。
1、找出所有 1 所在的行(列)索引;
2、最优点肯定为中位数的地方(如果 1 的个数是偶数个,那么最优点在中间的两个 1 其中任意一个);
3、分别计算行距离和纵距离,相加即可。
实现
class Solution{
int minTotalDistance(vector<int> v){
int res = 0;
std::sort(v.begin(), v.end());
int i = 0, j = v.size() - 1;
while (i < j){
res += (v[j--] - v[i++]);
}
return res;
}
public:
int minTotalDistance(vector<vector<int>>& grid){
vector<int> rows, cols;
for (int i = 0; i < grid.size(); ++i) {
for (int j = 0; j < grid[i].size(); ++j) {
if(grid[i][j] == 1){
rows.push_back(i);
cols.push_back(j);
}
}
}
return minTotalDistance(rows) + minTotalDistance(cols);
}
};
边栏推荐
猜你喜欢
随机推荐
字节一面:TCP 和 UDP 可以使用同一个端口吗?
linux安装部署redis&配置远程连接
二、junit接口自动化框架之二次开发
MySQL database
MySQL数据库的简介及select语句的执行流程
jupyter notebook 隐藏&显示全部输出内容
【 8.7 】 source code - card to LCM with GCD 】 【 】
二、pytest+selenium+allure实现web ui自动化
开源项目管理解决方案Leantime
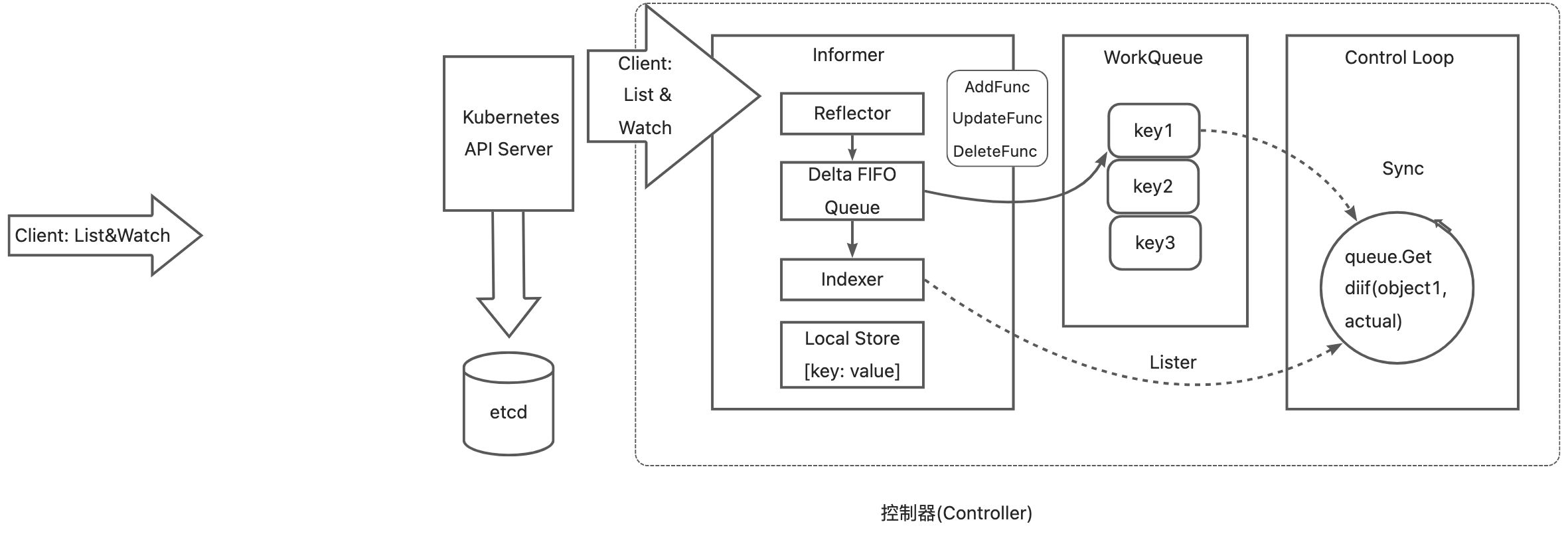
【云原生】云原生相关技术概念总结
Nervegrowold: machine advanced learning advice
题目:有序队列
垃圾账号不胜其烦,设备指纹快速发现
基于ECS实现一分钟自动化部署【华为云至简致远】
C#/VB.NET 将PDF转为PDF/X-1a:2001
多线程-并发编程
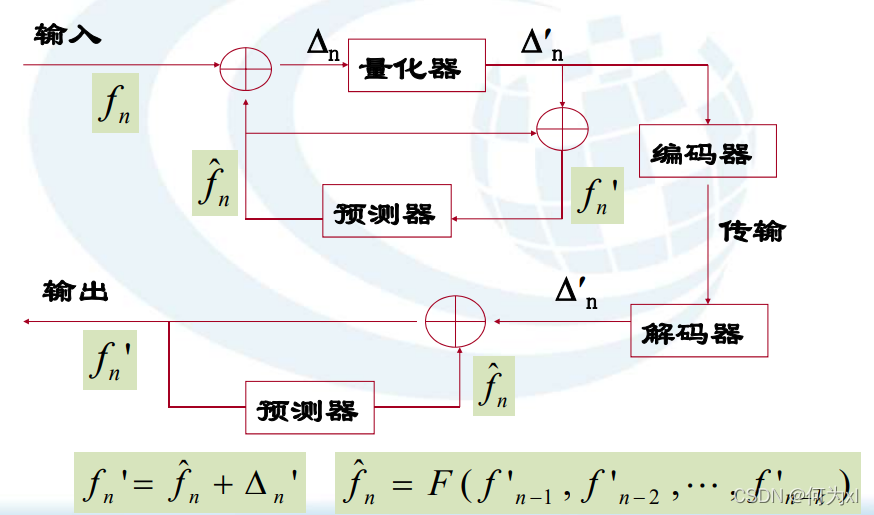
数字图像处理(六)—— 图像压缩
论文解读(soft-mask GNN)《Soft-mask: Adaptive Substructure Extractions for Graph Neural Networks》
Building and Visualizing Sudoku Games with Pygame
华为云分布式缓存服务Redis开通及使用规划教程【华为云至简致远】