当前位置:网站首页>【 8.4 】 source code - [math] [calendar] [delete library 】 【 is not a simple sequence (Bonus) 】
【 8.4 】 source code - [math] [calendar] [delete library 】 【 is not a simple sequence (Bonus) 】
2022-08-05 03:59:00 【ZhgDgE】
#47. 数学
题意:给定整数 n n n ,Fat professor wants to 1 ∼ n 1∼n 1∼n 这 n n n 个数字分成两组,Each group has at least one number,And make the greatest common divisor of the sum of the two sets of numbers the largest,Please output the largest greatest common divisor.
思路:首先 1 ∼ n × ( n + 1 ) 2 1\sim \frac {n\times (n+1)} 2 1∼2n×(n+1) Any number of can be represented by these numbers,Then the problem translates to having two positive integers satisfy a + b = m = n × ( n + 1 ) 2 a+b=m= \frac {n\times (n+1)} 2 a+b=m=2n×(n+1) ,最大化 gcd ( a , b ) \gcd(a,b) gcd(a,b)
Let's push the formula from the definition of tossing and dividing gcd ( a , b ) = gcd ( a , m − a ) = gcd ( a , m ) \gcd(a,b)=\gcd(a,m-a)=\gcd(a,m) gcd(a,b)=gcd(a,m−a)=gcd(a,m) , a a a 的取值为 a ∈ [ 1 , m − 1 ] a\in[1,m-1] a∈[1,m−1] ,Then the problem turns into finding m m m 的最大因子,Radical enumeration to find the smallest prime factor.
AC代码:http://oj.daimayuan.top/submission/317961
#913. 历法
题意:
题解:(数学) 代码源每日一题 Div1 历法
思路:和 这道题 挺像的.抽象一下:找到一对 x , y x,y x,y 满足 0 ≤ x , y < m i n ( m , d ) 0\leq x,y <min(m,d) 0≤x,y<min(m,d) 且 x × d + y = y × d + x ( m o d w ) x\times d+y=y\times d+x(\bmod w) x×d+y=y×d+x(modw) .化简一下, ( y − x ) × ( d − 1 ) = 0 ( m o d w ) (y-x)\times(d-1)=0(\bmod w) (y−x)×(d−1)=0(modw) ,即 w ∣ ( y − x ) × ( d − 1 ) w|(y-x)\times(d-1) w∣(y−x)×(d−1) ,把 d − 1 d-1 d−1 移到左边 w gcd ( w , d − 1 ) ∣ y − x \frac w {\gcd(w,d-1)}|y-x gcd(w,d−1)w∣y−x ,即 y = x ( m o d w gcd ( w , d − 1 ) ) y=x(\bmod \frac w {\gcd(w,d-1)}) y=x(modgcd(w,d−1)w) .我们把 [ 0 , m i n ( m , d ) ) [0,min(m,d)) [0,min(m,d)) into several congruent systems,Every congruence has it C c n t 2 C_{cnt}^2 Ccnt2 个贡献.计算一下即可.
总结了一下:
有连续的 n n n 个整数,Then these integers are modulo p p p 意义下,According to the size of the congruence system, it is divided into two types:
- 有 n % p n\%p n%p group congruence,大小为 ⌈ n p ⌉ \left \lceil \frac n p \right \rceil ⌈pn⌉
- 有 p − n % p p-n\%p p−n%p group congruence,大小为 ⌊ n p ⌋ \left \lfloor \frac n p \right \rfloor ⌊pn⌋
AC代码:http://oj.daimayuan.top/submission/318549
#855. 删库
题意:
题解:(贪心/字典树) 代码源每日一题 Div1 删库
思路:字典树上 dfs + 贪心.At the beginning, I forgot about the dictionary tree.
First we build the dictionary tree.We select a string and delete the corresponding string from the set,Equivalent to cutting a subtree from the dictionary tree,Marker points on the subtree ≤ k \leq k ≤k .
那么贪心思路就是:我们 dfs After finishing the son of a node,Count how many markers there are in the subtree.如果标记点 ≤ k \leq k ≤k ,Then our greedy strategy is to backtrack directly,Do not delete at this node,Because we can combine with markers on other sibling subtrees after backtracking,deleted together,minimize the number of deletions;反之,We must delete some child subtrees at this point.We sequentially delete the subtree with the largest number of markers,Makes backtracking with fewer markers.
AC代码:http://oj.daimayuan.top/submission/318499
#883. Uncomplicated numbers(Bonus)
题意:给定长度为 n ( 1 ≤ n ≤ 1 0 6 ) n(1\leq n\leq 10^6) n(1≤n≤106) 的序列 a ( 0 ≤ a ≤ 1 0 6 ) a(0\leq a\leq 10^6) a(0≤a≤106) ,Each operation can decrement a number by one,Add one to the number adjacent to this number.Ask the least number of operands to make the sequence gcd ( a ) ≥ 2 \gcd(a)\geq 2 gcd(a)≥2 .
题解:(枚举/贪心) 代码源每日一题 Div1 Uncomplicated numbers(Bonus)
思路:First there is a theorem:序列的 gcd \gcd gcd Equal to serial difference gcd \gcd gcd ,即 gcd ( a 1 , a 2 , ⋯ , a n − 1 , a n ) = gcd ( a 1 , a 2 − a 1 , ⋯ , a i − a i − 1 , ⋯ , a n − a n − 1 ) \gcd(a_1,a_2,\cdots,a_{n-1},a_n)=\gcd(a_1,a_2-a_1,\cdots,a_i-a_{i-1},\cdots,a_n-a_{n-1}) gcd(a1,a2,⋯,an−1,an)=gcd(a1,a2−a1,⋯,ai−ai−1,⋯,an−an−1) .同理,序列的 gcd \gcd gcd is equal to the sequence prefix sum gcd \gcd gcd .
Our operations on adjacent numbers of the sequence are equivalent to single-point addition or subtraction of the prefix and the sequence.我们枚举 s u m sum sum 的因子 x x x ,The question turns into how many times to operate so that each prefix is x x x 的倍数, ∑ i = 1 n − 1 min ( a i % p , p − a i % p ) \sum_{i=1}^{n-1}{\min(a_i\%p,p-a_i\%p)} ∑i=1n−1min(ai%p,p−ai%p) .
The problem solution is analogized from a classic problem.
给定两个序列 a , b a,b a,b ,It is also similar to the addition and subtraction of adjacent numbers,问对 a a a At least how many times the operation makes and b b b 完全相等.
定义 s t e p i step_i stepi 表示为前 i i i The minimum number of operations to be exactly equal,那么 s t e p i = s t e p i − 1 + ∣ s a i − s b i ∣ step_i=step_{i-1}+|sa_i-sb_i| stepi=stepi−1+∣sai−sbi∣ .可以理解为,当前面 i i i After the number operation is completed,会从 a i a_i ai Take this number here or send some numbers,We in order to make a i = b i a_i=b_i ai=bi ,Need to bring some numbers or send some numbers away a i + 1 a_{i+1} ai+1 ,The number of operations is ∣ s a i − s b i ∣ |sa_i-sb_i| ∣sai−sbi∣
边栏推荐
- 2022-08-04T17:50:58.296+0800 ERROR Announcer-3 io.airlift.discovery.client.Announcer appears after successful startup of presto
- 不看后悔,appium自动化环境完美搭建
- Redis1:Redis介绍、Redis基本特性、关系型数据库、非关系型数据库、数据库发展阶段
- YYGH-13-客服中心
- 冰蝎V4.0攻击来袭,安全狗产品可全面检测
- [CISCN2019 华东南赛区]Web11
- Android interview question - how to write with his hands a non-blocking thread safe queue ConcurrentLinkedQueue?
- Haproxy搭建Web群集
- [论文笔记] MapReduce: Simplified Data Processing on Large Clusters
- 队列题目:最近的请求次数
猜你喜欢

UE4 后期处理体积 (角色受到伤害场景颜色变淡案例)

Open-Falcon of operation and maintenance monitoring system

【8.1】代码源 - 【第二大数字和】【石子游戏 III】【平衡二叉树】
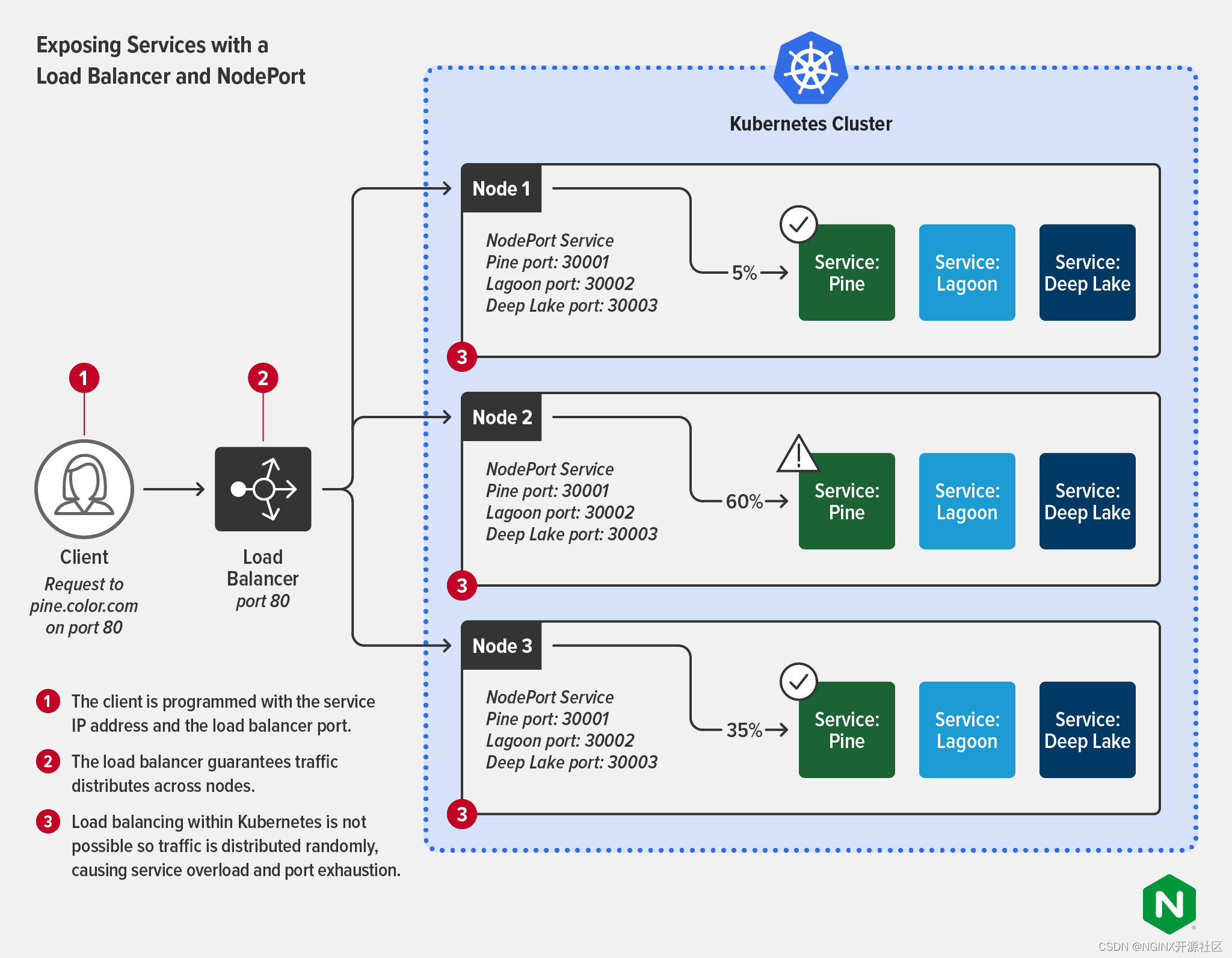
Getting Started with Kubernetes Networking

Web3.0 Dapps - the road to the future financial world

如何解决复杂的分销分账问题?

How do newcomers get started and learn software testing?

Solana NFT开发指南

UE4 通过重叠事件开启门

Industry Status?Why do Internet companies prefer to spend 20k to recruit people rather than raise their salary to retain old employees~
随机推荐
Swing有几种常用的事件处理方式?如何监听事件?
DEJA_VU3D - Cesium功能集 之 058-高德地图纠偏
关于#SQL#的迭代、父子结构查询问题,如何解决?
Based on holding YOLOv5 custom implementation of FacePose YOLO structure interpretation, YOLO data format conversion, YOLO process modification"
XMjs cross-domain problem solving
Redis1: Introduction to Redis, basic features of Redis, relational database, non-relational database, database development stage
4T硬盘剩余很多提示“No space left on device“磁盘空间不足
概率论的学习和整理8: 几何分布和超几何分布
【8.4】代码源 - 【数学】【历法】【删库】【不朴素的数列(Bonus)】
从企业的视角来看,数据中台到底意味着什么?
[MRCTF2020]Ezpop(详解)
Slapped in the face: there are so many testers in a certain department of byte
2022软件测试工程师最全面试题
How to discover a valuable GameFi?
UE4 通过与其它Actor互动开门
阿里本地生活单季营收106亿,大文娱营收72亿,菜鸟营收121亿
Call Alibaba Cloud oss and sms services
token、jwt、oauth2、session解析
Hard power or soft power, which is more important to testers?
bytebuffer 内部结构