当前位置:网站首页>哈夫曼编码
哈夫曼编码
2022-04-21 13:23:00 【若悲浪】
前言
哈夫曼编码是根据一段数据的成员的占比,来对其编码,频率高的成员编码应该尽量短,这样整体所占的内存就比固定长度编码要小。
| 字母 | A | B | C | D | E |
|---|---|---|---|---|---|
| 普通编码 | 000 | 001 | 010 | 011 | 100 |
那么一个长度为N的字符串,仅由ABCDE组成,进行编码,则占用3N位空间大小。
哈夫曼树
假如一个长度为26的字符串中,A有2个,B有3个,C有6个,D有7个,E有8个。
(1)首先找到出现频率最小的,即A和B,将它们作为一个新的结点AB的左右孩子,频率小的作为左孩子,大的作为右孩子。新的结点AB则包含A和B,出现的频率为5。
(2)现在频率最小的是AB和C,它们再组成一个子树,新结点ABC的频率为11。
(3)当前各部分的频率分别为ABC(11)、D(7)、E(8),因此D和E组成新的子树,新结点DE的频率为15。
(4)最后ABC和DE组成哈夫曼树,ABC为左子树,DE为右子树。
(5)将树的左分支权值设为0,右分支权值设为1。
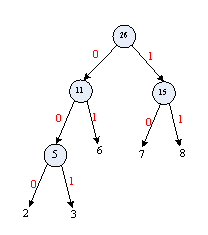
哈夫曼编码
我们将从哈夫曼树的树根到叶子所经过的路径作为叶子的编码。
| 字母 | A | B | C | D | E |
|---|---|---|---|---|---|
| 哈夫曼编码 | 000 | 001 | 01 | 10 | 11 |
普通编码所占用的空间大小:3 × \times × 26 = 78。
哈夫曼编码所占用的空间大小:3 × \times × 2 + 3 × \times × 3 + 2 × \times × 6 + 2 × \times × 7 + 2 × \times × 8 = 57。
减小了27%的存储空间大小。
哈夫曼树的创建
思路:
(1)首先树的创建,应该先定义树的结点;
(2)结点的成员包括此结点的权重weight,初始化为0;以及该结点的左右孩子,这里以结点在数组中位置表示,亦可以用指针表示,初始化为-1;
(3)为了方便从叶向根遍历,因此需要访问其父节点,因此包括parent成员,初始化为-1。
class Node
{
public:
int lchild = -1, rchild = -1;
int parent = -1;
int weight = 0;
};
然后我们从键盘输入权重:
void InitWeight(Node *p, int num)
{
for (int i = 0; i < num; i++)
{
int weight;
cout << i << " Weight: " ;
cin >> weight;
p[i].weight = weight;
}
cout << "---------------Finish !------------------" << endl;
}
寻找最小两结点,合并结点
在叶子结点数组尾部加上N-1位合并结点,每次在没有父结点的结点中,找到权值最小的两个结点,将其合并。

思路:
(1)先找到第一个根结点(无父结点,parent = -1),暂将其权重作为最小值
(2)遍历所有根结点,通过比较,找到权重最小的结点,min1等于其在数组的位置。
(3)找到第二个根结点(不等于min1),暂将其权重作为第二小值;
(4)遍历除min1以外的所有根结点,找到权重最小的结点,min2等于其在数组的位置。
void SearchMin(const Node *p, int num, int &min1, int &min2)
{
for (int i = 0; i < num; i++) //找到第一个根结点
{
if (p[i].parent == -1)
{
min1 = i;
break;
}
}
for (int i = 0; i < num; i++) //遍历全部根结点,找到权重最小的根结点
{
if ((p[i].parent == -1) && (p[i].weight < p[min1].weight))
{
min1 = i;
}
}
for (int i = 0; i < num; i++) //找到第二个根结点
{
if ((p[i].parent == -1) && (i != min1))
{
min2 = i;
break;
}
}
for (int i = 0; i < num; i++) //遍历全部根结点,找到权重第二小的根结点
{
if ((p[i].parent == -1) && (p[i].weight < p[min2].weight) && (i != min1))
{
min2 = i;
}
}
}
创建哈夫曼树
思路:
(1)在前numLeafs + i个结点中寻找权重最小的结点,numLeafs + i为当前包含叶子结点和合并结点的个数。
(2)将找到的两个结点,合并结点,新结点为这两个结点的父结点。
void CreateHuffman(Node *p, int numLeafs)
{
int PosMin1, PosMin2;
InitWeight(p, numLeafs);
for (int i = 0; i < numLeafs - 1; i++)
{
SearchMin(p, numLeafs + i, PosMin1, PosMin2); //权重最小的两个结点PosMin1和PosMin2
//合并结点
p[numLeafs + i].weight = p[PosMin1].weight + p[PosMin2].weight;
p[numLeafs + i].lchild = PosMin1;
p[numLeafs + i].rchild = PosMin2;
p[PosMin1].parent = numLeafs + i;
p[PosMin2].parent = numLeafs + i;
}
}
编码转换
思路:
从每个叶结点向根结点遍历,因此是从下往上遍历,因此如果是左分支,则在编码串的最前端插入0,如果是右分支,则插入1。
void HuffmanCode(Node *p, const int num, string *codes)
{
int parent;
for (int i = 0; i < num; i++)
{
int j = i;
while (p[j].parent != -1) // 从所有叶结点开始,向根结点遍历
{
parent = p[j].parent;
if (p[parent].lchild == j) // 如果为左分支,则在codes[i]字符串最前处插入0
{
codes[i].insert(codes[i].begin(),'0');
}
else // 如果为右分支,则插入1
{
codes[i].insert(codes[i].begin(),'1');
}
j = parent;
}
}
}
主函数
#include <iostream>
#include <iomanip>
#include <string.h>
using namespace std;
#define NUM (5)
int main(void)
{
Node N[2*NUM - 1]; //定义结点数组
CreateHuffman(N, NUM); //构建哈夫曼树
string codes[NUM]; //定义编码串数组
HuffmanCode(N, NUM, codes); //哈夫曼编码
cout << "哈夫曼编码:" << endl;
for (int i = 0; i < NUM; i++) //打印哈夫曼编码
{
cout << N[i].weight << setw(8) << codes[i] << endl;
}
return 0;
}
输出:
0 Weight: 6
1 Weight: 7
2 Weight: 3
3 Weight: 2
4 Weight: 8
---------------Finish !------------------
哈夫曼编码:
6 01
7 10
3 001
2 000
8 11
版权声明
本文为[若悲浪]所创,转载请带上原文链接,感谢
https://blog.csdn.net/qq_41563510/article/details/124316892
边栏推荐
- OJ daily practice - output new array in reverse order
- Skills of layout design
- The course of qiniu business school allows Xiaobai to open an account to buy national debt reverse repurchase. Is it safe?
- 36 day assault Tencent finally took the offer! Redis, high concurrency
- Revit secondary development - creating grids (phase 9)
- Creating host elements of Revit secondary development (doors and windows, etc.) (issue 14)
- [digital signal processing] linear constant coefficient difference equation (determine whether the system is a "linear time invariant system" according to "linear constant coefficient difference equat
- Network communication protocol model
- 14 tips for making your code better
- no server suitable for synchronization found
猜你喜欢

必选项输入内容后红色星号消失

LLVM之父Chris Lattner:编译器的黄金时代

Redis data persistence

美创科技受邀为海淀区教育科学研究院开展数据安全培训

Go language file operation

Chris LATTNER, father of llvm: the golden age of compilers

How do we media create hot articles and improve reading volume
![[csnote] DB exception (redundant data, modification exception, deletion exception, insertion exception)](/img/28/adf0221ed9b25e5f0c3229441f30a2.png)
[csnote] DB exception (redundant data, modification exception, deletion exception, insertion exception)

In depth analysis of focal loss loss function
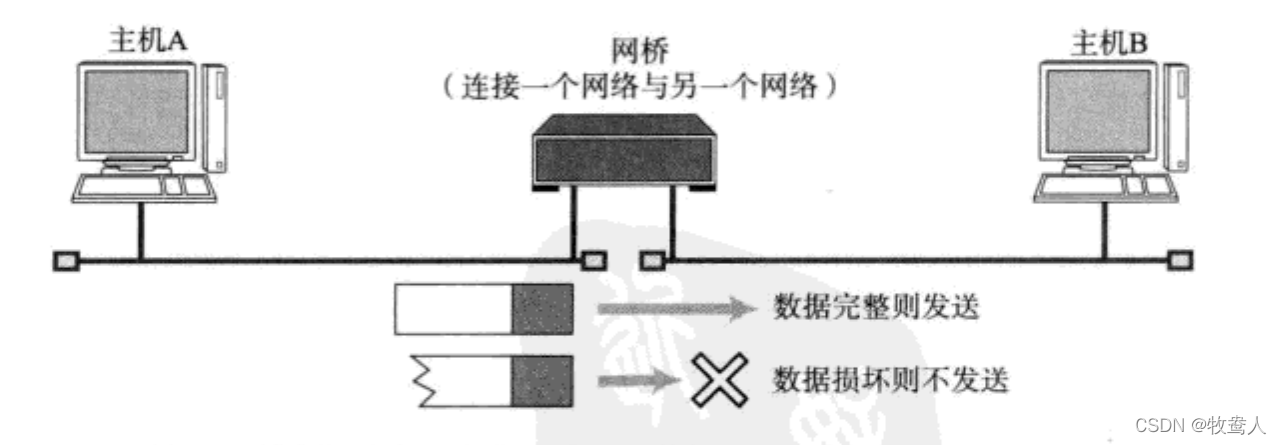
网络的构成要素
随机推荐
Underlying principle of high concurrent IO
How to install the database of Dameng 8 version in Kirin V10 SP2
通信滑动窗口
网络的构成要素
no server suitable for synchronization found
After the completion of hundreds of millions of yuan of financing, smart bank plans to land urban intelligent driving products in more than 100 cities
Filter and listener listeners
MySQL uses PIP and binlog2sql to install
Redis data persistence
53W words! Ali's first system performance optimization guide is so fragrant that it can be called the optimal solution of performance optimization
leetcode:824. 山羊拉丁文【简单字符串操纵】
Convert m3u8 format to MP4 through fmpeg
[digital signal processing] correlation coefficient (concept of correlation coefficient | energy signal and power signal | causality of system)
Configuring VRRP (Virtual Router Redundancy Protocol) with Cisco
UGUI-- Button 按钮组件
安装和配置Canal
20210812
万字干货!帮你深度掌握设计中的「光影」知识点
Introduction to Revit secondary development -- program debugging with hellorexport (phase IV)
搭建服务注册与发现中心