当前位置:网站首页>数学-求和符号的性质
数学-求和符号的性质
2022-08-05 02:48:00 【Code_LT】
1. 单重求和
∑ i = 1 n f ( x i ) = f ( x 1 ) + f ( x 2 ) + ⋯ + f ( x n ) \sum_{i=1}^nf(x_i)=f(x_1)+f(x_2)+\cdots+f(x_n) i=1∑nf(xi)=f(x1)+f(x2)+⋯+f(xn)
1.1 性质1,提取公因式
若 h ( y , z ) h(y,z) h(y,z)的取值和x无关,则有:
∑ i = 1 n h ( y , z ) f ( x i ) = h ( y , z ) ∑ i = 1 n f ( x i ) \sum_{i=1}^nh(y,z)f(x_i)=h(y,z)\sum_{i=1}^nf(x_i) i=1∑nh(y,z)f(xi)=h(y,z)i=1∑nf(xi)
将变量 i i i写成 x i x_i xi更形象:
∑ x i h ( y , z ) f ( x i ) = h ( y , z ) ∑ x i f ( x i ) \sum_{x_i}h(y,z)f(x_i)=h(y,z)\sum_{x_i}f(x_i) xi∑h(y,z)f(xi)=h(y,z)xi∑f(xi)
上面有了简写,实际上 x i ∈ X x_i \in X xi∈X, X = { x 1 , x 2 , ⋯ , x n } X=\{x_1,x_2,\cdots,x_n\} X={ x1,x2,⋯,xn}:
∑ x i ∈ X 通常可简写为 ∑ x i ,表示累加所有 x i 可取的值 \sum_{x_i \in X}通常可简写为\sum_{x_i},表示累加所有x_i可取的值 xi∈X∑通常可简写为xi∑,表示累加所有xi可取的值
2. 多重求和
以两重求和为例:
∑ i = 1 n ∑ j = 1 m f ( x i ) h ( y j ) = f ( x 1 ) ∑ j = 1 m h ( y j ) + f ( x 2 ) ∑ j = 1 m h ( y j ) + ⋯ + f ( x n ) ∑ j = 1 m h ( y j ) = 再展开就省略不写了 \sum_{i=1}^n\sum_{j=1}^mf(x_i)h(y_j)=f(x_1)\sum_{j=1}^mh(y_j)+f(x_2)\sum_{j=1}^mh(y_j)+\cdots+f(x_n)\sum_{j=1}^mh(y_j)=再展开就省略不写了 i=1∑nj=1∑mf(xi)h(yj)=f(x1)j=1∑mh(yj)+f(x2)j=1∑mh(yj)+⋯+f(xn)j=1∑mh(yj)=再展开就省略不写了
2.1 性质1,符号顺序可换
两重:
∑ i = 1 n ∑ j = 1 m f ( x i ) h ( y j ) = ∑ j = 1 m ∑ i = 1 n f ( x i ) h ( y j ) \sum_{i=1}^n{\color{red} \sum_{j=1}^m}f(x_i)h(y_j)={\color{red} \sum_{j=1}^m}\sum_{i=1}^nf(x_i)h(y_j) i=1∑nj=1∑mf(xi)h(yj)=j=1∑mi=1∑nf(xi)h(yj)
注意,当某个求和的范围受另一个变量限制时,符号交换律就不适用了,如:
∑ i = 1 n ∑ j = 1 i f ( x i ) h ( y j ) ≠ ∑ j = 1 i ∑ i = 1 n f ( x i ) h ( y j ) \sum_{i=1}^n\sum_{j=1}^{\color{red} i}f(x_i)h(y_j) {\color{red} \neq}\sum_{j=1}^ {\color{red} i}\sum_{i=1}^nf(x_i)h(y_j) i=1∑nj=1∑if(xi)h(yj)=j=1∑ii=1∑nf(xi)h(yj)
多重:
∑ x i ∑ y j ∑ z k f 1 ( x i ) f 2 ( y j ) f 3 ( z k ) = ∑ z k ∑ y j ∑ x i f 1 ( x i ) f 2 ( y j ) f 3 ( z k ) \sum_{x_i}\sum_{y_j}\sum_{z_k}f_1(x_i)f_2(y_j)f_3(z_k)=\sum_{z_k}\sum_{y_j}\sum_{x_i}f_1(x_i)f_2(y_j)f_3(z_k) xi∑yj∑zk∑f1(xi)f2(yj)f3(zk)=zk∑yj∑xi∑f1(xi)f2(yj)f3(zk)
f 1 ( x i ) f 2 ( y j ) f 3 ( z k ) f_1(x_i)f_2(y_j)f_3(z_k) f1(xi)f2(yj)f3(zk)可看做一个函数 f ( x 1 , x 2 , x 3 ) f(x_1,x_2,x_3) f(x1,x2,x3),则得到更通用的形式:
∑ x i ∑ y j ∑ z k f ( x 1 , x 2 , x 3 ) = ∑ z k ∑ y j ∑ x i f ( x 1 , x 2 , x 3 ) \sum_{x_i}\sum_{y_j}\sum_{z_k}f(x_1,x_2,x_3)=\sum_{z_k}\sum_{y_j}\sum_{x_i}f(x_1,x_2,x_3) xi∑yj∑zk∑f(x1,x2,x3)=zk∑yj∑xi∑f(x1,x2,x3)
牢记可调换的前提:x,y,z的取值范围,相互没有影响。
2.1 性质2,符号可分别求
有时候,为了求解的方便,我们并不希望函数 f ( x 1 , x 2 , x 3 ) f(x_1,x_2,x_3) f(x1,x2,x3)写成一个整体,而是拆开后分别求值。
∑ x i ∑ y j ∑ z k f 1 ( x i ) f 2 ( y j ) f 3 ( z k ) = ∑ x i f 1 ( x i ) ∑ y j f 2 ( y j ) ∑ z k f 3 ( z k ) \sum_{x_i}\sum_{y_j}\sum_{z_k}f_1(x_i)f_2(y_j)f_3(z_k)=\sum_{x_i}f_1(x_i)\sum_{y_j}f_2(y_j)\sum_{z_k}f_3(z_k) xi∑yj∑zk∑f1(xi)f2(yj)f3(zk)=xi∑f1(xi)yj∑f2(yj)zk∑f3(zk)
x,y,z的取值范围也要满足相互没有影响,可通过展开计算进行简单的证明。
上述性质的好处在于,可将复杂的问题分成三个部分分别计算,再求乘积。
( ∑ x i f 1 ( x i ) ) ( ∑ y j f 2 ( y j ) ) ( ∑ z k f 3 ( z k ) ) {\color{red}(\sum_{x_i}f_1(x_i))} {\color{green}(\sum_{y_j}f_2(y_j))} {\color{blue}(\sum_{z_k}f_3(z_k))} (xi∑f1(xi))(yj∑f2(yj))(zk∑f3(zk))
边栏推荐
猜你喜欢
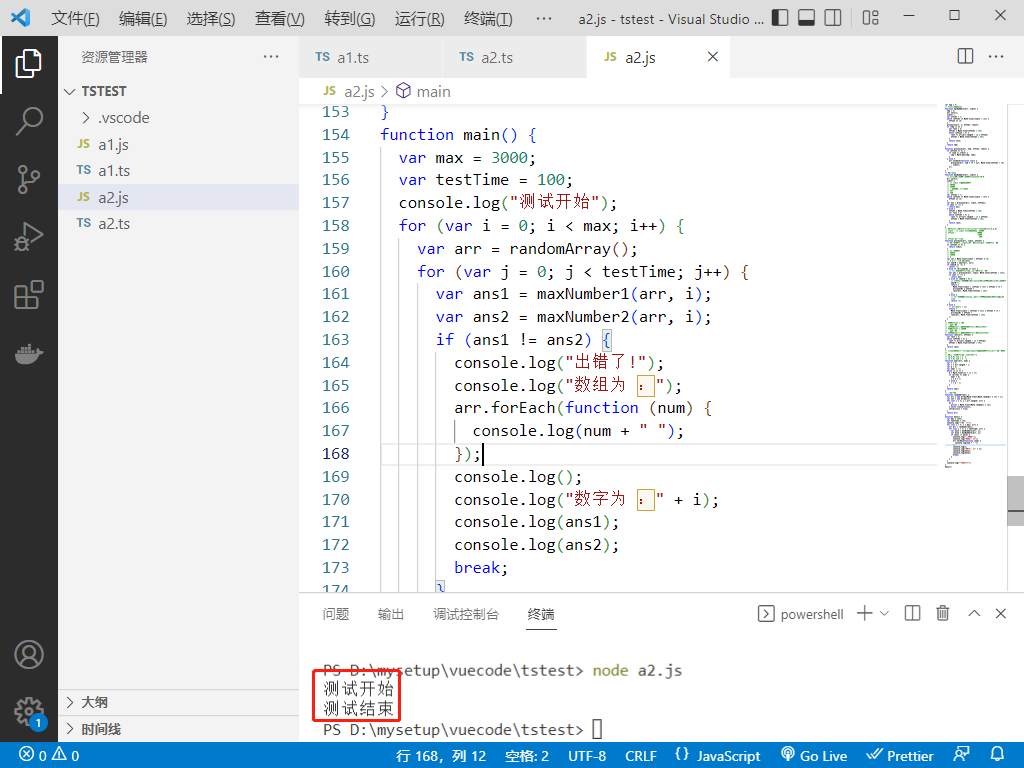
2022-08-04:输入:去重数组arr,里面的数只包含0~9。limit,一个数字。 返回:要求比limit小的情况下,能够用arr拼出来的最大数字。 来自字节。

使用二维码传输文件的小工具 - QFileTrans 1.2.0.1
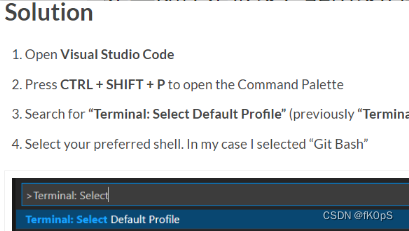
VSCode Change Default Terminal how to modify the Default Terminal VSCode
leetcode 15

View handler stepping record

dmp(dump)转储文件

Question about #sql shell#, how to solve it?

Everyone in China said data, you need to focus on core characteristic is what?

The Tanabata copywriting you want has been sorted out for you!

Multithreading (2)
随机推荐
627. 变更性别
倒计时 2 天|云原生 Meetup 广州站,等你来!
Access Characteristics of Constructor under Inheritance Relationship
leetcode - a subtree of another tree
2022-08-04: Input: deduplicated array arr, the numbers in it only contain 0~9.limit, a number.Return: The maximum number that can be spelled out with arr if the requirement is smaller than limit.from
1527. Patients suffering from a disease
[Fortune-telling-60]: "The Soldier, the Tricky Way"-2-Interpretation of Sun Tzu's Art of War
Apache DolphinScheduler, a new generation of distributed workflow task scheduling platform in practice - Medium
Compressed storage of special matrices
金仓数据库如何验证安装文件平台正确性
View handler stepping record
QT语言文件制作
[In-depth study of 4G/5G/6G topic-51]: URLLC-16-"3GPP URLLC related protocols, specifications, and technical principles in-depth interpretation"-11-High reliability technology-2-Link adaptive enhancem
QStyle平台风格
private封装
OpenGL 工作原理
Hash table lookup (hash table)
QT language file production
sql server installation prompts that the username does not exist
J9 Digital Currency: What is the creator economy of web3?