Discrete probability distribution

Geometric distribution

A situation ： Chad likes skiing , But the technology is not good . Slide from the top of the mountain to the bottom of the slope , The probability of no accident is 0.2（ Assuming Chad doesn't improve ）. If he's going to keep trying , Until it's done . After the first success , He will stop skiing .

So what is the probability that he will successfully slide to the bottom of the slope if he tries to slide once or twice ？

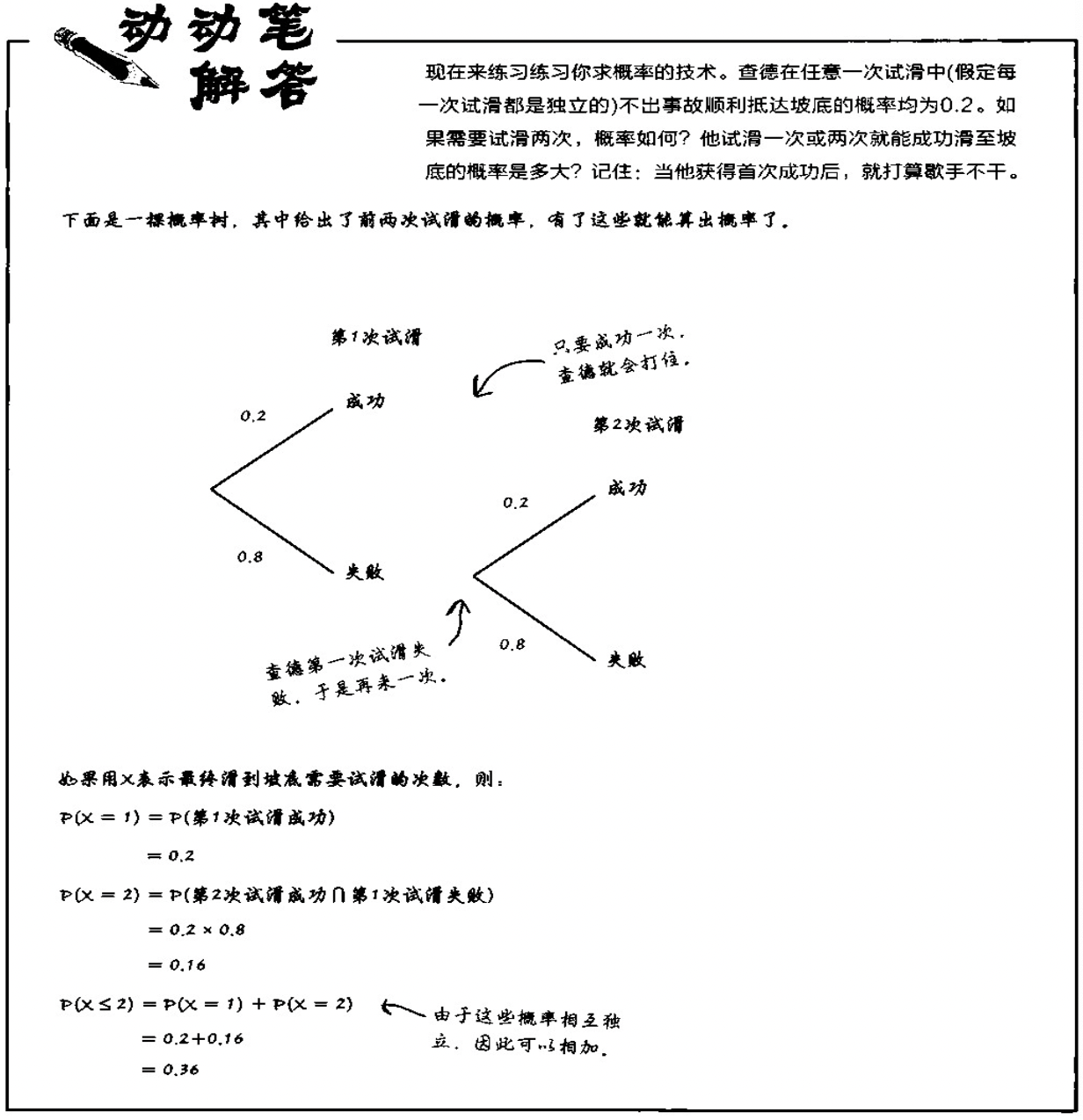
Then if he can try endless times , How many times will he succeed ？ We can deduce （ You can imagine the probability tree ,0.8 It's a case of failure ）：

there r Is the value of the deduction , and x Is any value in the probability distribution , Don't confuse the two .

You can see , Chaddy r The probability of success is ：
$$P(X=r)=0.8^{r-1}\ast 0.2$$
Let's summarize . If you use p Represents the success probability of a single test slip , The probability of failure is 1-p, We call this probability q, Therefore, any probability with this property can be calculated by the following formula ：
$$P(X=r)=q^{r-1}p$$
This formula is called probability Geometric distribution .

The geometric distribution contains the following conditions ：

1. Go through a series of Are independent of each other Test of .
2. Every experiment has the possibility of success , There is also the possibility of failure , And the success probability of a single test is the same .
3. Your main interest is , How many experiments are needed to achieve the first success .

If the above conditions are met in the case of seeking probability , Then you can use the formula of geometric distribution to help you make a quick decision .

Tips ： there “ success ” It means Events of interest to us Become a fact . If the events we want to see have negative implications , From a statistical point of view , This negative event can still be regarded as a “ success ” event .

To find out X Take a specific value r Probability , The following formula can be used for fast calculation ：
$$P(X=r)=p{q}^{r-1}$$
among p For the probability of success ,q=1-p Is the probability of failure . namely , For the first time r The experiment was successful , First, fail (r-1) Time .

When r=1 when ,P(X=r) To the maximum , With r increase ,P(X=r) Gradual decline . It means that the probability of success is the greatest in the first experiment .

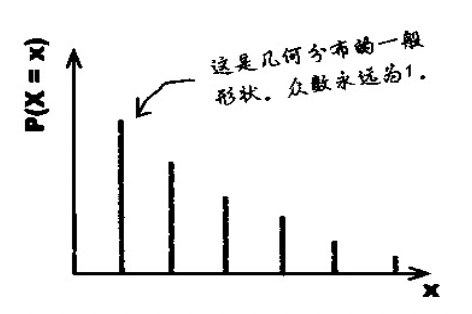
Geometric distribution in the case of inequality

The number of tests is greater than r, Means before r This time must fail .
$$P(X>r)=q^r$$
that , In order to achieve a success, you need to try r Time or r The following probability ：
$$\begin{gathered} \because P(X\le r)+P(X>r)=1 \\ \therefore P(X\le r)=1-P(X>r)=1-q^r \end{gathered}$$
If a variable X The probability of conforms to the geometric distribution , And the success probability of a single test is p, You can write ：
$$X\sim Geo(p)$$

The expected pattern of geometric distribution

Previously, we have calculated the number of times Chad needs to try to slide to the bottom of the slope , But what about expectation and variance ？ When mathematical expectations are known , We can get Chad's expectation of the number of test slides before he succeeds .

The expected formula is $E(X)=\sum xP(X=x)$, In this case, there are infinite probabilities . however , We can calculate the first few values first , See if there is some fixed pattern .

Here is x The first few values of , among X~Geo(0.2)

The first 3 Columns are intermediate values , The value represents $xP(X=x)$. But in x=5 When , The value is the highest . The first 4 Columns are expectations . When x Greater than 5 when , The first 3 Column - The median is getting smaller and smaller . There is little to change expectations later .

Here's number one 4 Column （$xP(X\le x)=\sum xP(X=x)$ = expect ） The graphic ：

take xP(X=x) The cumulative sum of （ expect ） After drawing a figure , It can be seen that , With x Bigger , Expect to get closer and closer to a specific value ：5（ I understand it ： With x More and more , The ordinate is getting closer and closer 5）. After countless tests （ A great deal of x【 Not very “ Big ” Of x】） after ,xP(X=x) Cumulative total of （ That is, expectations ） Exactly equal to 5, namely $E(X)=5$.

The meaning of the above formula is very intuitive ： The probability of success of a single test is 0.2, It can be understood as 5 One of the attempts tends to succeed , So we can expect Chad to try 5 You can succeed once .

The above situation can be generalized to any value p. If X~Geo§, be ：
$$E(X)=\frac{1}{p}$$

Variance of geometric distribution

Premise ：$FangBad=Var(X)=E(X^2)-E^2(X)$

Look at the table below , The first 4 The column is $x^{2}P(X\le x)=E(X^2)=\sum x^{2}P(X=x)$, The first 3 Column is $x^{2}P(X=x)$.

[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-VhBVS1tn-1650331163542)( Discrete probability distribution .assets/image-20220415220708530.png)]

stay x achieve 10 Before and after ,$x^{2}P(X=x)$ Increase first and then decrease .

So if you find the variance , The variance formula is ：$Var(X)=E(X^2)-E^2(X)$, According to the... Of the previous figure 4 The expected square of the column sum and the previous figure , Subtracting the , You can find the variance . At this time, draw another one by x A growing image ,

With x Bigger ,$x^{2}P(X\le x)-E^2(X)$ Getting closer to a specific value , Here is 20.

Just like when discussing mathematical expectations , The law of variance can be summarized as follows . If X～Geo§, be
$$Var(X)=\frac{q}{p^2}$$

Summary of geometric distribution

ask ： Why does geometric distribution use p and q？

answer ：p Stands for English words “probability”, namely “ probability ”, In geometric distribution , It represents the success probability of a single test .q In statistics, it often represents 1-p, That is to say p’. These letters will appear in large numbers in this chapter and later in this book .

Example ,“ success ” Events for “ Successfully slide to the bottom of the slope ”.