当前位置：网站首页>AVL树的插入操作
AVL树的插入操作
2022-08-09 15:07:00 【爱学代码的学生】
目录
1. 什么是AVL树？
二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查
找元素相当于在顺序表中搜索元素，效率低下。因此，两位俄罗斯的数学家G.M.Adelson-Velskii
和E.M.Landis在1962年发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。
一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：
它的左右子树都是AVL树
左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
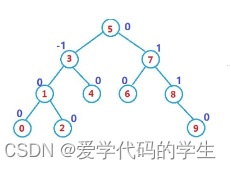
1.1 AVL树结点的定义
template<class K,class V>
struct AVLTreeNode
{
pair<K, V> _kv; //插入的数据
AVLTreeNode<K, V>* _left; //左孩子
AVLTreeNode<K, V>* _right;//右孩子
AVLTreeNode<K, V>* _parent;//双亲
//右子树-左子树的高度差
int _bf; //balance factor
//构造函数
AVLTreeNode(const pair<K,V>& kv)
:_kv(kv)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_bf(0)
{}2. AVL树的插入
AVL树的插入就是建立在二叉搜索树的基础上添加了平衡因子，因此AVL树也是二叉搜索树的一种，那么AVL树的插入分为两步：
1. 按照二叉搜索树的方式来插入结点
2. 调节结点的平衡因子
1. 按照二叉搜索树的方式来插入
//如果是首次插入
if (!_root)
{
_root = new Node(kv);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
//这里和普通的二叉搜索树插入差不多
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (kv.first < parent->_kv.first)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
//只不过多了一个三叉链
cur->_parent = parent;
2. 调节平衡因子
当新结点插入搜索树中可能回破坏AVL的平衡性，这时就需要更新平衡因子来判断是否破坏了平衡性。在插入新结点之前，父节点的平衡因子只能是0、1、-1这三种情况，而插入之后我们就需要先更新父节点的平衡因子：
1. 如果插入的结点在父节点的左边 : 平衡因子 - 1
2. 如果插入的结点在父节点的右边 : 平衡因子 + 1
此时父节点的平衡因子可能有三种情况：0、正负1、正负2：
1. 如果此时父节点的平衡因子的0，则说明插入结点后的高度没有发生改变，则不需要调整父节点以上的结点的平衡因子
2. 覆盖此时父节点的平衡因子是正负1，则说明插入结点后高度发生了改变，需要调整父节点以上的结点的平衡因子
3. 如果此时的父节点的平衡因子是正负2，则说明不满足AVL树的性质，需要对其进行旋转
我们先写出更新平衡因子的代码：
//更新平衡因子
while (parent)
{
//先更新目前父节点的平衡因子
if (cur == parent->_left)
{
parent->_bf--;
}
else
{
parent->_bf++;
}
//如果高度不变则退出
if (parent->_bf == 0)
{
break;
}
//如果有一边变高了，则需要继续往上进行修改
else if (parent->_bf == -1 || parent->_bf == 1)
{
cur = cur->_parent;
parent = parent->_parent;
}
//如果超出了平衡因子，则需要进行旋转
else if (parent ->_bf == 2 || parent-> _bf == -2)
{
//旋转操作....
break;
}
//在插入之前，此树就已经发生了平衡因子失调的情况
else
{
assert(false);
}
}那么接下来我们要考虑旋转的问题
3. AVL树的旋转
如果在一棵原本平衡的树中插入了一个新结点，可能会引起不平衡，此时必须调整树的结构，使其平衡化，而结点插入的位置不同，也导致了旋转分成了四类情况：
3.1 新结点插入较高左子树的左边 - 右单旋
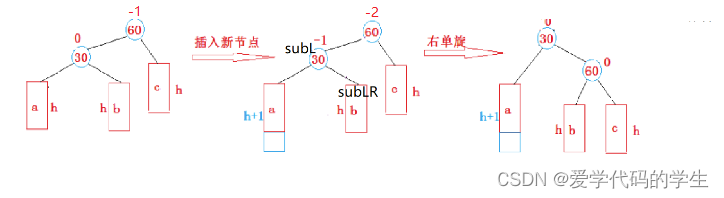
这里我们可以看见60这个结点已经不满足AVL树的性质了，那么我们要如何处理呢？
首先60(parent)的位置就是我们的旋转点，60的左子树称为subL，subL的右子树称为subLR
我们将parent的左子树指向subLR，subL的右子树指向parent：
代码实现如下：
//右右旋转
//需要将左子树的右子树接在父节点的左子树上，左子树的右子树变成父节点
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
//父节点接右子树的左子树
parent->_left = subLR;
if (subLR)
{
subLR->_parent = parent;
}
//左子树的右子树变成父节点
Node* ppnode = parent->_parent;//父节点的父节点
subL->_right = parent;
parent->_parent = subL;
//如果父节点是根节点
if (parent == _root)
{
_root = subL;
//根节点的父节点为空
subL->_parent = nullptr;
}
//如果父节点不是根节点
else
{
if (parent == ppnode->_left)
{
ppnode->_left = subL;
}
else
{
ppnode->_right = subL;
}
subL->_parent = ppnode;
}
//更新旋转后的平衡因子
subL->_bf = 0;
parent->_bf = 0;
}3.2 新结点插入较高右子树的右边 - 左单旋
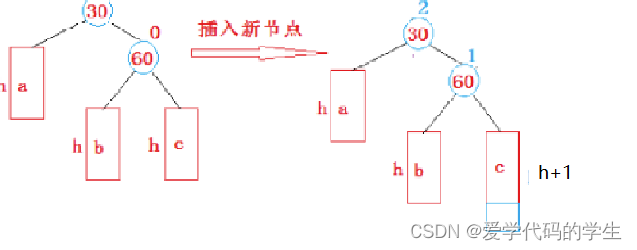
这里我们可以看见30这个结点已经不满足AVL树的性质了，那么我们要如何处理呢？
首先30(parent)的位置就是我们的旋转点，将30的右子树称为subR，subR的左子树称为subRL。
我们将30的右子树指向subRL，将subR的左子树指向parent：
代码实现如下：
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
//父节点接右子树的左子树
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
//右子树的左子树变成父节点
Node* ppnode = parent->_parent;//父节点的父节点
subR->_left = parent;
parent->_parent = subR;
//如果父节点是根节点
if (parent == _root)
{
_root = subR;
//根节点的父节点为空
subR->_parent = nullptr;
}
//如果父节点不是根节点
else
{
if (parent == ppnode->_left)
{
ppnode->_left = subR;
}
else
{
ppnode->_right = subR;
}
subR->_parent = ppnode;
}
//更新旋转后的平衡因子
subR->_bf = 0;
parent->_bf = 0;
}3.3 新结点插入较高左子树的右边 -左右双旋
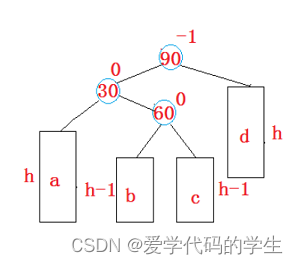
当我们的结点插入在b或者c位置或者当h=0时会发生平衡失调
实现步骤：
先以30为旋转点进行左单旋，然后再以90为旋转点进行右单旋
但是由于结点插入的位置有两个：一个是b一个是c，对于插入不同的位置，旋转后各个结点的平衡因子会发生变化
首先我们来看插入在b的情况：
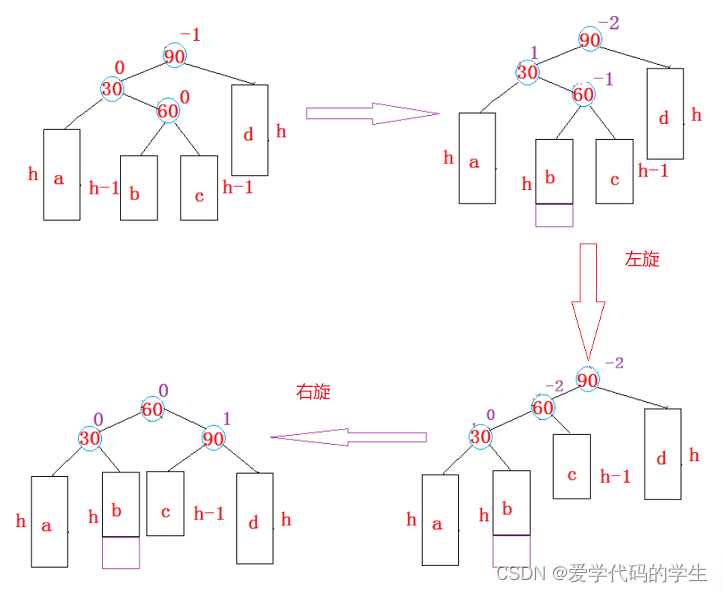
我们可以发现当插入在b位置时，旋转前60位置的平衡因子是-1，旋转后60(subLR)位置的平衡因子是-1时，30(subL)最后的平衡因子是0，90(parent)是1
然后来看插入在c位置时的情况：
我们可以发现当插入在c位置时，旋转前60位置的平衡因子是1，旋转后60(subLR)位置的平衡因子是0时，30(subL)最后的平衡因子-1，90(parent)是0
最后来看当h为0的情况下：
我们可以发现当h==0时，旋转前60位置的平衡因子是0，旋转后60(subLR)位置的平衡因子是0时，30(subL)最后的平衡因子是0，90(parent)是0
因此根据subLR的平衡因子的三种情况：1,-1,0,最后修改的平衡因子也不同
代码实现如下：
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;
RotateL(subL);
RotateR(parent);
if (bf == 0)
{
subL->_bf = 0;
subLR->_bf = 0;
parent->_bf = 0;
}
else if (bf == -1)
{
subL->_bf = 0;
subLR->_bf = 0;
parent->_bf = 1;
}
else if (bf == 1)
{
subL->_bf = -1;
subLR->_bf = 0;
parent->_bf = 0;
}
else
{
//在执行之前此树就有问题
assert(false);
}
}3.4 新结点插入较高右子树的左边 -右左双旋
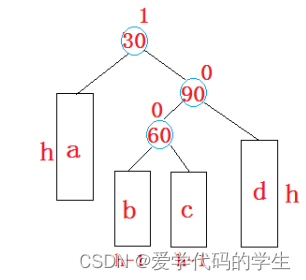
当我们结点插入在b、c位置会发生失调
实现步骤：
先以90为旋转点进行右单旋，然后再以30为旋转点进行左单旋
但是由于结点插入的位置有两个：一个是b一个是c，对于插入不同的位置，旋转后各个结点的平衡因子会发生变化
首先我们来看插入在b的情况：
我们可以发现当插入在b位置时，旋转前60位置的平衡因子是-1，旋转后60(subLR)位置的平衡因子是0时，30(subL)最后的平衡因子是0，90(parent)是1
然后来看插入在c位置时的情况：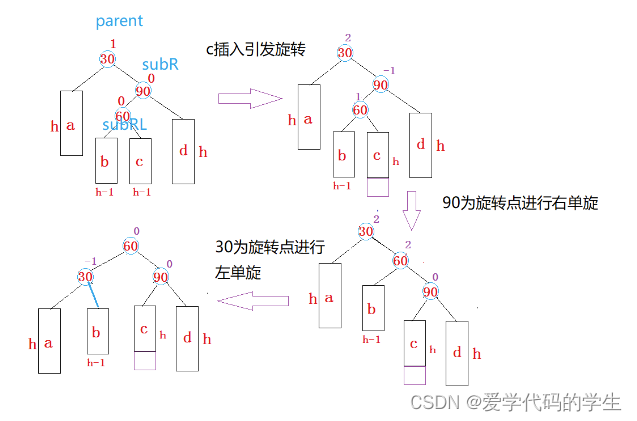
我们可以发现当插入在b位置时，旋转前60位置的平衡因子是-1，旋转后60(subLR)位置的平衡因子是0时，30(subL)最后的平衡因子是-1，90(parent)是0
最后来看当h为0的情况下：
我们可以发现当h==0时，旋转前60位置的平衡因子是0，旋转后60(subLR)位置的平衡因子是0时，30(subL)最后的平衡因子是0，90(parent)是0
代码实现如下：
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(subR);
RotateL(parent);
if (bf == 0)
{
subR->_bf = 0;
subRL->_bf = 0;
parent->_bf = 0;
}
else if (bf == -1)
{
subR->_bf = 1;
subRL->_bf = 0;
parent->_bf = 0;
}
else if (bf == 1)
{
subR->_bf = 0;
subRL->_bf = 0;
parent->_bf = -1;
}
else
{
//在执行之前此树就有问题
assert(false);
}
}总结
假如以parent为根的子树不平衡，即parent的平衡因子为2或者-2，分以下情况考虑
1. parent的平衡因子为2，说明parent的右子树高，设parent的右子树的根为pSubR
- 当pSubR的平衡因子为1时，执行左单旋
- 当pSubR的平衡因子为-1时，执行右左双旋
2. parent的平衡因子为-2，说明parent的左子树高，设parent的左子树的根为pSubL
- 当pSubL的平衡因子为-1是，执行右单旋
- 当pSubL的平衡因子为1时，执行左右双旋
旋转完成后，原parent为根的子树个高度降低，已经平衡，不需要再向上更新。
最后代码：
bool insert(const pair<K,V>& kv)
{
//1. 按照搜索树的规则插入
//2. 看看是否违背了平衡因子
if (!_root)
{
_root = new Node(kv);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
//这里和普通的二叉搜索树插入差不多
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (kv.first < parent->_kv.first)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
//只不过多了一个三叉链
cur->_parent = parent;
//更新平衡因子
while (parent)
{
//先更新目前父节点的平衡因子
if (cur == parent->_left)
{
parent->_bf--;
}
else
{
parent->_bf++;
}
//如果高度不变则退出
if (parent->_bf == 0)
{
break;
}
//如果有一边变高了，则需要继续往上进行修改
else if (parent->_bf == -1 || parent->_bf == 1)
{
cur = cur->_parent;
parent = parent->_parent;
}
//如果超出了平衡因子，则需要进行旋转
else if (parent ->_bf == 2 || parent-> _bf == -2)
{
if (parent->_bf == 2 && cur->_bf == 1)//左单旋
{
RotateL(parent);
}
if (parent->_bf == -2 && cur->_bf == -1)//右单旋
{
RotateR(parent);
}
if (parent->_bf == -2 && cur->_bf == 1)//左右双旋
{
RotateLR(parent);
}
if (parent->_bf == 2 && cur->_bf == -1)//右左双旋
{
RotateRL(parent);
}
break;
}
//在插入之前，此树就已经发生了平衡因子失调的情况
else
{
assert(false);
}
}
}
边栏推荐
- Why does a four-byte float represent a wider range than an eight-byte long
- uniapp封装全局js并在页面引用
- 第四章：使用本地地理空间数据（4.1-4.5）
- 0. About The Author And Preface
- 排序相关：数组的相对排序、最小的k个数（快排）、合并区间、翻转对 ...
- C语言的常量和操作符
- C语言扫雷
- 初始C语言（2） C生万物
- 【建模必胜秘籍】往届国赛建模方法 2021高教社杯 国赛数学建模
- Heap series_0x0A: 3 methods to solve the heap overflow problem at once
猜你喜欢
随机推荐
js实现滑动条验证
动态规划套题：零钱兑换、完全平方数
第二章：创建交互式地图（2.4-2.6）
The first day of the real in CSDN
分布式恢复【进阶篇】
float属性的使用
第一章：GEE 和 GEEMAP
Chapter 4: Using Local Geospatial Data (4.1-4.5)
js中的Date对象 及 将时间戳转换为yy-mm-dd hh:mm:ss格式的方法
五.初始指针
js和jq实现点击小眼睛后密码显示与隐藏切换
【完美解决v-if导致echart不显示问题】
六.数组越界问题引出对栈区内存的探索
(十)打包和项目部署
2022华数杯C题：插层熔喷非织造材料的性能控制研究 - 思路
良匠-手把手教你写NFT抢购软（一）
1. Introducing GEE and Geemap
4. Using Local Geospatial Data
【建模必胜秘籍】往届国赛建模方法 2021高教社杯 国赛数学建模
如何设置边框圆角