当前位置:网站首页>Decomposition of matrix -- LU decomposition
Decomposition of matrix -- LU decomposition
2022-04-22 07:05:00 【Lupin123123】
LU decompose
LU Decomposition is a kind of matrix decomposition , Decompose a matrix into a Lower triangular matrix And a Upper triangular matrix The product of the , Sometimes you need to multiply by a permutation matrix .
LU Decomposition can be regarded as Gauss elimination Matrix form of . In numerical calculation ,LU Decomposition is often used to solve linear equations 、 And it is a key step in finding the inverse matrix and calculating the determinant .
One 、 Definition
For squares A A A, A A A Of LU Decomposition is to decompose it into a lower triangular matrix L And upper triangular matrix U The product of the , That is to say A = L U A=LU A=LU.
For example, a 3 × 3 {\displaystyle 3\times 3} 3×3 Matrix A A A , Its LU The decomposition will be written in the following form :
A = [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] = [ l 11 0 0 l 21 l 22 0 l 31 l 32 l 33 ] [ u 11 u 12 u 13 0 u 22 u 23 0 0 u 33 ] {\displaystyle A={\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{bmatrix}}={\begin{bmatrix}l_{11}&0&0\\l_{21}&l_{22}&0\\l_{31}&l_{32}&l_{33}\\\end{bmatrix}}{\begin{bmatrix}u_{11}&u_{12}&u_{13}\\0&u_{22}&u_{23}\\0&0&u_{33}\\\end{bmatrix}}} A=⎣⎡a11a21a31a12a22a32a13a23a33⎦⎤=⎣⎡l11l21l310l22l3200l33⎦⎤⎣⎡u1100u12u220u13u23u33⎦⎤
LDU decompose
Matrix A Of LDU Decomposition is to decompose it into a unit lower triangular matrix L、 Diagonal matrix D And unit upper triangular matrix U The product of the , namely A = L D U {\displaystyle A=LDU} A=LDU
Among them, the unit is 、 The lower triangular matrix means that the diagonal is full of 1 Above 、 Lower triangular matrix . in fact ,LDU Decomposition can be extended to A It's a general matrix , Not a square matrix .
Existence and uniqueness
- One Invertible matrix Can be done LU Decompose if and only if its All subexpressions are nonzero .
- If one of them is required L matrix ( or U matrix ) Is a unit triangular matrix , So decomposition is the only .
- Even if the matrix is irreversible ,LU There may still be . actually , If a rank is k The front of the matrix k A sequential principal is not zero , Then it can LU decompose , But not the other way around .
Two 、 Algorithm
LU Decomposition is essentially an expression of Gauss elimination method . Is essentially take A It is transformed into an upper triangular matrix by elementary row transformation , Its transformation matrix is a unit lower triangular matrix . This is the so-called durritt algorithm (Doolittle algorithm), From bottom to top, the matrix A Do elementary line transformation , Change the element at the bottom left of the diagonal to zero , Then it is proved that the effect of these row transformations is equivalent to left multiplying a series of unit lower triangular matrices , The inverse of the product of this series of unit lower triangular matrices is L matrix , It is also a unit lower triangular matrix .
Durritt algorithm
For given N × N matrix A = ( a n , n ) {\displaystyle A=(a_{n,n})} A=(an,n) Yes A ( 0 ) : = A A^{
{(0)}}:=A A(0):=A
Then define for n = 1 , . . . , N − 1 n = 1,...,N-1 n=1,...,N−1 The situation is as follows :
In the n Step , Elimination matrix A ( n − 1 ) A^{(n-1)} A(n−1) Of the n The elements below the main diagonal of the column : take A ( n − 1 ) A^{(n-1)} A(n−1) Of the n Line times l i , n = − a i , n ( n − 1 ) a n , n ( n − 1 ) {\displaystyle l_{i,n}=-{\frac {a_{i,n}^{(n-1)}}{a_{n,n}^{(n-1)}}}} li,n=−an,n(n−1)ai,n(n−1) Then add to the second i i i Go up . among i = n + 1 , … , N {\displaystyle i=n+1,\ldots ,N} i=n+1,…,N. This is equivalent to A ( n − 1 ) A^{(n-1)} A(n−1) Multiply the left side of by a unit lower triangular matrix :
L n = [ 1 0 ⋱ 1 l n + 1 , n ⋱ ⋮ ⋱ 0 l N , n 1 ] {\displaystyle L_{n}={\begin{bmatrix}1&&&&&0\\&\ddots &&&&\\&&1&&&\\&&l_{n+1,n}&\ddots &&\\&&\vdots &&\ddots &\\0&&l_{N,n}&&&1\\\end{bmatrix}}} Ln=⎣⎢⎢⎢⎢⎢⎢⎢⎡10⋱1ln+1,n⋮lN,n⋱⋱01⎦⎥⎥⎥⎥⎥⎥⎥⎤
therefore , set up A ( n ) = L n A ( n − 1 ) {\displaystyle A^{(n)}=L_{n}A^{(n-1)}} A(n)=LnA(n−1) after N-1 After wheel operation , All coefficients below the main diagonal are 0 了 , So we get an upper triangular matrix A(N-1), Then there is :
A = L 1 − 1 L 1 A ( 0 ) = L 1 − 1 A ( 1 ) = L 1 − 1 L 2 − 1 L 2 A ( 1 ) = L 1 − 1 L 2 − 1 A ( 2 ) = … = L 1 − 1 … L N − 1 − 1 A ( N − 1 ) {\displaystyle A=L_{1}^{-1}L_{1}A^{(0)}=L_{1}^{-1}A^{(1)}=L_{1}^{-1}L_{2}^{-1}L_{2}A^{(1)}=L_{1}^{-1}L_{2}^{-1}A^{(2)}=\ldots =L_{1}^{-1}\ldots L_{N-1}^{-1}A^{(N-1)}} A=L1−1L1A(0)=L1−1A(1)=L1−1L2−1L2A(1)=L1−1L2−1A(2)=…=L1−1…LN−1−1A(N−1)
At this time , matrix A ( N − 1 ) A^{(N-1)} A(N−1) Namely U, L = L 1 − 1 … L N − 1 − 1 {\displaystyle L=L_{1}^{-1}\ldots L_{N-1}^{-1}} L=L1−1…LN−1−1. Lower triangular matrix L k {\displaystyle L_{k}} Lk The inverse of is still a lower triangular matrix , And the product of the lower triangular matrix is still the lower triangular matrix , therefore L {\displaystyle L} L It's a lower triangular matrix . So we get to decompose : A = L U {\displaystyle A=LU} A=LU.
obviously , If the algorithm works , In each step of operation, there must be a n , n ( n − 1 ) ≠ 0 {\displaystyle a_{n,n}^{(n-1)}\neq 0} an,n(n−1)=0. If this condition does not hold , It's going to take the first n One line exchanges with another , There will be a Permutation matrix P. That's why, in general LU The reason why there will be a permutation matrix in the decomposition .
Example :
Put a simple 3×3 matrix A Conduct LU decompose :
A = [ 1 2 3 2 5 7 3 5 3 ] {\displaystyle A={\begin{bmatrix}1&2&3\\2&5&7\\3&5&3\\\end{bmatrix}}} A=⎣⎡123255373⎦⎤
First, put the elements in the first column of the matrix a 11 a_{11} a11 All of the following elements become 0, namely
L 1 A = [ 1 0 0 − 2 1 0 − 3 0 1 ] × [ 1 2 3 2 5 7 3 5 3 ] = [ 1 2 3 0 1 1 0 − 1 − 6 ] {\displaystyle L_{1}A={\begin{bmatrix}1&0&0\\-2&1&0\\-3&0&1\\\end{bmatrix}}\times {\begin{bmatrix}1&2&3\\2&5&7\\3&5&3\\\end{bmatrix}}={\begin{bmatrix}1&2&3\\0&1&1\\0&-1&-6\\\end{bmatrix}}} L1A=⎣⎡1−2−3010001⎦⎤×⎣⎡123255373⎦⎤=⎣⎡10021−131−6⎦⎤
Then add the elements in the second column of the matrix a 22 a_{22} a22 All of the following elements become 0, namely
L 2 ( L 1 A ) = [ 1 0 0 0 1 0 0 1 1 ] × [ 1 2 3 0 1 1 0 − 1 − 6 ] = [ 1 2 3 0 1 1 0 0 − 5 ] = U {\displaystyle L_{2}(L_{1}A)={\begin{bmatrix}1&0&0\\0&1&0\\0&1&1\\\end{bmatrix}}\times {\begin{bmatrix}1&2&3\\0&1&1\\0&-1&-6\\\end{bmatrix}}={\begin{bmatrix}1&2&3\\0&1&1\\0&0&-5\\\end{bmatrix}}=U} L2(L1A)=⎣⎡100011001⎦⎤×⎣⎡10021−131−6⎦⎤=⎣⎡10021031−5⎦⎤=U
L = L 1 − 1 L 2 − 1 = [ 1 0 0 2 1 0 3 0 1 ] × [ 1 0 0 0 1 0 0 − 1 1 ] = [ 1 0 0 2 1 0 3 − 1 1 ] {\displaystyle L=L_{1}^{-1}L_{2}^{-1}={\begin{bmatrix}1&0&0\\2&1&0\\3&0&1\\\end{bmatrix}}\times {\begin{bmatrix}1&0&0\\0&1&0\\0&-1&1\\\end{bmatrix}}={\begin{bmatrix}1&0&0\\2&1&0\\3&-1&1\\\end{bmatrix}}} L=L1−1L2−1=⎣⎡123010001⎦⎤×⎣⎡10001−1001⎦⎤=⎣⎡12301−1001⎦⎤
版权声明
本文为[Lupin123123]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204220604096445.html
边栏推荐
- 阻抗标注你遇到崩溃吗?
- 替代 FE1.1s HUB读卡主控芯片-MA8601
- The last day of 2018, welcome 2019.
- 什么样的设计才是有把握的?
- 统计2015-2017年间911中的类别
- 在消防联网(楼宇、工厂、海上风电、管廊等)中CAN光纤转换器、CAN总线光端机典型应用案例
- 很难相信,这对高速信号换了那么多次过孔!!!
- Ma8608 Qiyan USB 2.0 High Speed 4-port USB hub controller chip scheme
- 你相信有一天BGA里面不能走差分线吗?
- Tencent cloud Internet of things - gateway device experience
猜你喜欢

911数据中不同月份不同类型的电话的次数的变化情况

It's nothing to be able to dismantle the host. Mr. expressway can also test it

Easy to use textview marquee effect

如果有一种设计不增加成本又能改善信号质量

在消防联网(楼宇、工厂、海上风电、管廊等)中CAN光纤转换器、CAN总线光端机典型应用案例
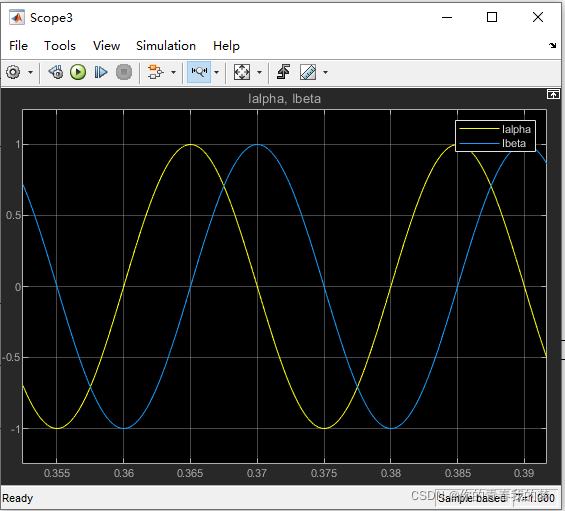
PMSM FOC控制 Matlab/Simulink仿真之反Park变换

Ag9310mcq supports the design reference circuit of mother seat forward and reverse plug typec to HDMI projection scheme

Typec转HDMI 4K30HZ扩展芯片方案CS5261和CS5266设计参数及电路对比

Development of two stage target detection technology (I) r-cnn and spp net
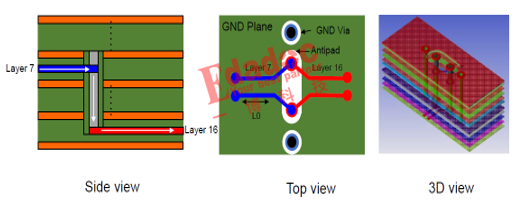
深度解说信号孔旁边到底需要几个地过孔
随机推荐
MDK scope joint debugging RTT mode multi-channel
USBCAN卡在动力电池组EOL测试系统中CAN总线的应用
TD041S485H完全兼容ISO3080, ISO3086 ISO3082, ISO3088
I've gone too far, but I can't get out of the routine of ddrx debugging
No such file or directory include "XXXXXX. H"“
阻抗标注你遇到崩溃吗?
How many ground vias are needed next to the depth interpretation signal hole
Is there any difference in the worst impedance processing you have encountered?
[蓝桥杯复习] 直线
FreeRTOS v10.1.0源码中文注释版
DP to HDMI scheme | cs5216 Scheme Application | cs5216 design scheme
SSS1700
HDMI切换器方案|3进1出HDMI切换器|5进1出HDMI2.0切换器AG7111设计电路
Cs5213 new specification | cs5213 new specification | HDMI to VGA with audio signal output scheme design
Glide conflicts with picture selector Matisse after 4.0.0
替代AG9311设计电路|CS5266方案应用电路图|Typec扩展坞三合一方案设计开发
量化5个城市的PM2.5随时间的变化情况
It's hard to believe that this pair of high-speed signals have changed through holes so many times!!!
Various commonly used tools status bar cache conversion to obtain app information clipboard file operation encryption and decryption operation
Display the up and down floating ripple animation according to the size of the sound shell