当前位置:网站首页>信息学奥赛一本通 1211:判断元素是否存在 | OpenJudge 1.13 41:判断元素是否存在
信息学奥赛一本通 1211:判断元素是否存在 | OpenJudge 1.13 41:判断元素是否存在
2022-04-22 07:04:00 【君义_noip】
【题目链接】
ybt 1211:判断元素是否存在
OpenJudge 1.13 41:判断元素是否存在
【题目考点】
1. 递归
【解题思路】
解法1:递归
如果 y y y是集合中的元素,那么 2 y + 1 2y+1 2y+1与 3 y + 1 3y+1 3y+1都是该集合中的元素。
反过来想,如果 x x x是集合中的元素,以下两种情况至少有一种成立:
- 如果 x − 1 x-1 x−1能整除 2 2 2,那么 ( x − 1 ) / 2 (x-1)/2 (x−1)/2是该集合中的元素
- 如果 x − 1 x-1 x−1能整除 3 3 3,那么 ( x − 1 ) / 3 (x-1)/3 (x−1)/3是该集合中的元素
递归思路为:
-
递归问题:判断 n n n是不是集合中的元素
-
递归关系:
- 如果 n − 1 n-1 n−1能整除 2 2 2,判断 ( n − 1 ) / 2 (n-1)/2 (n−1)/2是不是该集合中的元素。
- 如果 n − 1 n-1 n−1能整除 3 3 3,判断 ( n − 1 ) / 3 (n-1)/3 (n−1)/3是不是该集合中的元素。
两种情况只要有一种成立,那么 n n n就是该集合中的元素。
-
递归出口:如果 n n n为 k k k,那么 n n n是该集合中的元素。如果 n < 0 n<0 n<0,则 n n n不是该集合中的元素。
【题解代码】
解法1:递归
#include<bits/stdc++.h>
using namespace std;
int k, x;
bool solve(int n)//判断n是不是集合M中的元素
{
if(n == k)
return true;
else if(n < 0)
return false;
bool b1 = (n-1)%2 == 0 ? solve((n-1)/2) : false;//如果不能整除,直接得到false结果
bool b2 = (n-1)%3 == 0 ? solve((n-1)/3) : false;
return b1 || b2;
}
int main()
{
char c;
cin >> k >> c >> x;
cout << (solve(x) ? "YES" : "NO");
return 0;
}
版权声明
本文为[君义_noip]所创,转载请带上原文链接,感谢
https://blog.csdn.net/lq1990717/article/details/124335410
边栏推荐
猜你喜欢

Dual optical port 1 + 1 backup 8-way E1 + 2-way Gigabit isolation network 4-way 100m isolation PDH optical transceiver

LabVIEW 2012中的收藏选板导入到LabVIEW 2013

MySQL advanced view -- View introduction, view crud syntax, check options (cascaded, local), view update, view function, view case
![FileNotFoundError: [Errno 2] No such file or directory](/img/ea/0c3f2768d14c1f4bb42bd1309ab996.png)
FileNotFoundError: [Errno 2] No such file or directory
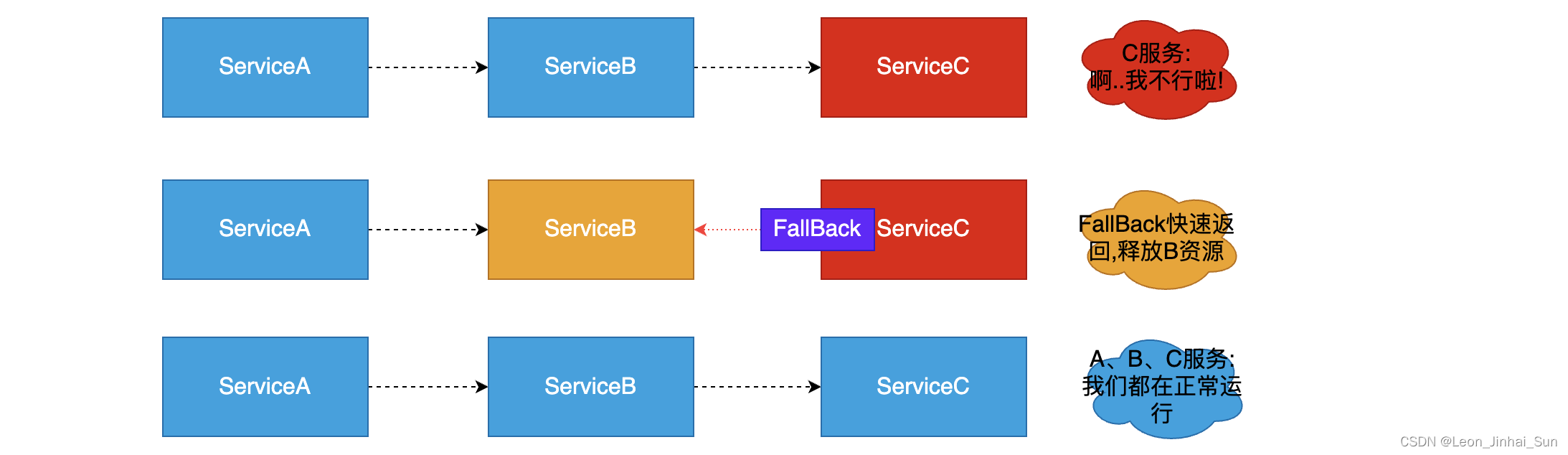
分布式系统服务熔断
laravel 新建路由文件

PHP 实现 QQ 登录

Carrier grade double optical port protection 8e1 + 4-way physical isolation gigabit network optical transceiver 1000m network 100m optical transceiver
TP5 发送邮件(2020-05-27)

PDH光端机4路E1+4路百兆以太网 4路2M光端机 FC单纤20公里 机架式
随机推荐
氨基(-NH2)酞菁铜 cas: 28632-30-6 (四氨基酞菁)铜(II) 四氨基酞菁铜(CuTAPc)的多种叫法-齐岳生物小编分享
汉源高科8路多业务PDH光端机双光口保护+8路E1+4路千兆以太网+4路百兆网络电口
TP5 多条件where查询(使用PHP变量)
tf.keras.layers.InputLayer函数
软件测试面试题汇总
tf.keras.layers.TimeDistributed函数
迎接稳定币3.0时代 USDD带来金融创新
Shrio study notes (II)
牛客白月赛6【题解】
金九银十面试季,字节跳动面试题拿走不谢(附详细答案解析)
jmeter_mysql 数据库连接
openFeign 服务调用
4E1+2路千兆隔离网络+4路百兆物理隔离网络PDH光端机
网络原理二(上)
简历上怎样写期望薪资,才能让你面试时工资翻倍?
SQL 语句——DDL
服务雪崩效应
tf.keras.layers.Dense函数
Monkey introduction operation
Unity 透视投影矩阵变换的可视化