前言

给你一个整数数组 nums 和一个整数 k ，找出三个长度为 k 、互不重叠、且全部数字和（3 * k 项）最大的子数组，并返回这三个子数组。

以下标的数组形式返回结果，数组中的每一项分别指示每个子数组的起始位置（下标从 0 开始）。如果有多个结果，返回字典序最小的一个。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/maximum-sum-of-3-non-overlapping-subarrays
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

一、解题思路

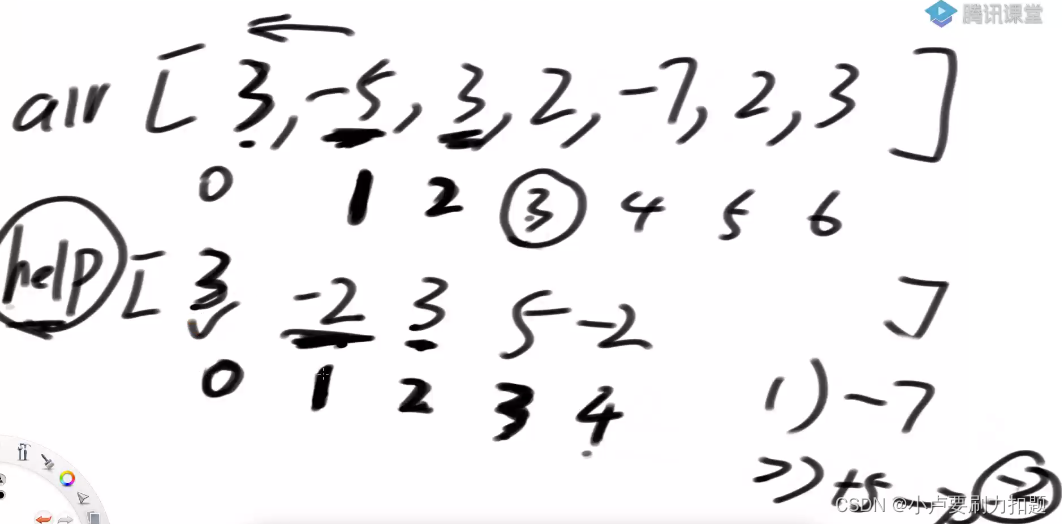
help数组
help[1]:子数组必须以1位置数结尾情况下,累加和怎么最好
第一种可能性:只包含-5
第二种可能性: -5决定往左扩
help的含义是子数组必须以0位置的数结尾的情况下最好收益是啥?
子数组必须以1位置的数结尾的情况下最好收益是啥?
子数组必须以2位置的数结尾的情况下最好收益是啥?
…
然后利用help数组求dp数组

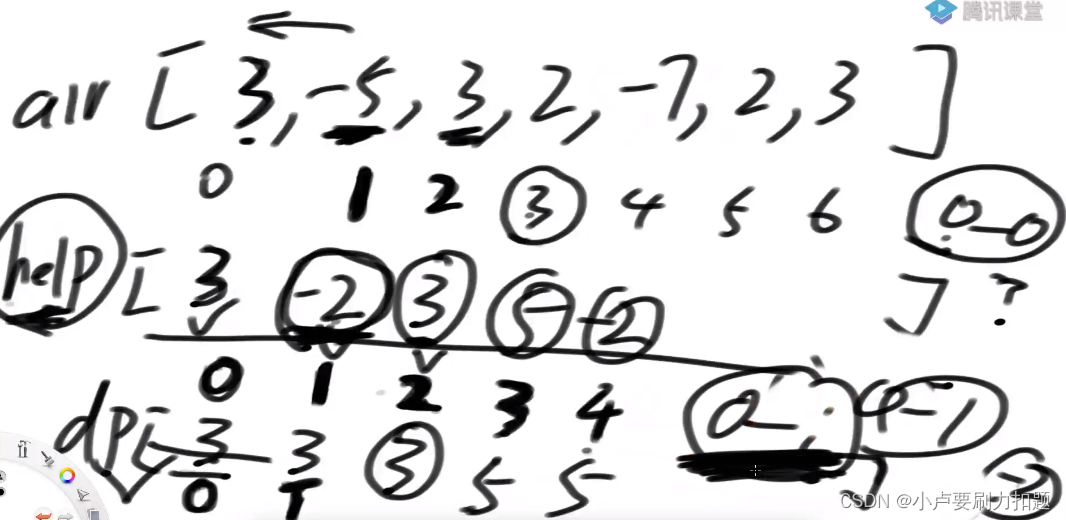
dp数组
dp[0]: 0~0范围上随意选，累加和怎么最好
dp[1]:
子数组必须以1结尾,最好收益是-2
子数组不以1位置结尾情况下怎么最好,就是之前的答案3
两种可能性求最大值
dp[i]: 0~i范围上随意选，子数组的累加和怎么最好

	public static int maxSumLenK(int[] arr, int k) {
    
		int N = arr.length;
		// 子数组必须以i位置的数结尾，长度一定要是K，累加和最大是多少？
		// help[0] help[k-2] ...
		int sum = 0;
		for (int i = 0; i < k - 1; i++) {
    
			sum += arr[i];
		}
		// 0...k-2 k-1 sum
		int[] help = new int[N];
		for (int i = k - 1; i < N; i++) {
    
			// 0..k-2 
			// 01..k-1
			sum += arr[i];
			help[i] = sum;
			// i == k-1 
			sum -= arr[i - k + 1];
		}
		// help[i] - > dp[i] 0-..i K

	}

原问题题解

原问题:必须选3个非空子数组，长度一定是K, 无重合，累加和最大.
整个数组从左往右遍历生成dp数组
再从右往左生成dp数组: i~N-1范围上,如果只选一个子数组… 累加和怎么最大

让L到R的距离为K,L…R是中间的子数组，k=3
问题变为中间数组必须是3~ 5的话，0~ 2范围和6~12范围上怎么选一个子数组最好,
左右两边的信息直接查表可以得到
第一回, L来到3, R来到5,我们查0~ 2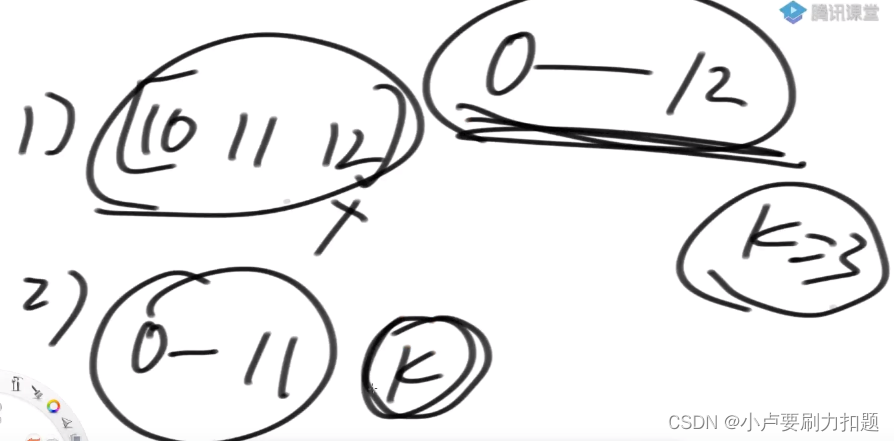

0-12范围上K-定是长度为3的数组，有那些可能性
1)就是10.11,12三个数组成的子数组.
2)子数组不以12结尾就是0-11范围上选K个在0~12范围上
就怎么选K个

代码

class Solution {
    
    public int[] maxSumOfThreeSubarrays(int[] nums, int k) {
    
        int n=nums.length;
        int[] range=new int[n];
        int[] left=new int[n];
        int sum=0;
        for(int i=0;i<k;i++){
    
            sum+=nums[i];
        }
        range[0]=sum;
        left[k-1]=0;
        int max=sum;
        for(int i=k;i<n;i++){
    
            sum = sum - nums[i - k] + nums[i];
			range[i - k + 1] = sum;
			left[i] = left[i - 1];
			if (sum > max) {
    
				max = sum;
				left[i] = i - k + 1;
			}
        }
        sum=0;
        for(int i=n-1;i>=n-k;i--){
    
            sum+=nums[i];
        }
        max=sum;
        int[] right=new int[n];
        right[n-k]=n-k;
        for(int i=n-k-1;i>=0;i--){
    
            sum=sum-nums[i+k]+nums[i];
            right[i]=right[i+1];
            if(sum>=max){
    
                max=sum;
                right[i]=i
;            }
        }
        int a=0;
        int b=0;
        int c=0;
        max=0;
        for(int i=k;i<n-2*k+1;i++){
    
            int part1=range[left[i-1]];
            int part2=range[i];
            int part3=range[right[i+k]];
            if(part1+part2+part3>max){
    
                max = part1 + part2 + part3;
				a = left[i - 1];
				b = i;
				c = right[i + k];
            }
        }
        return new int[] {
     a, b, c };
    }
}