当前位置:网站首页>【Complete Backpack with Restrictions】Educational Codeforces Round 133 (Rated for Div. 2) D. Chip Move
【Complete Backpack with Restrictions】Educational Codeforces Round 133 (Rated for Div. 2) D. Chip Move
2022-08-07 17:25:00 【solego】
题意:
给定 n n n 和 k k k,初始步长为 k k k ,每次可以走 k k k multiples of steps,next time go ( k + 1 ) (k+1) (k+1)multiples of steps,以此类推,问从 0 0 0 开始到达 [ 1 , n ] [1,n] [1,n] The number of scenarios per point.
题解:
When only taking double the number of steps each time, ( s t e p + k ) × ( s t e p − k + 1 ) 2 ≤ n \frac{(step+k)\times (step-k+1)}{2}\leq n 2(step+k)×(step−k+1)≤n,So at most just go O ( n ) O(\sqrt{n}) O(n)次.
The problem is transformed into a complete knapsack problem with constraints,走第 i i i 次前,must have gone 1 1 1 到 i − 1 i-1 i−1次
f [ i ] [ j ] f[i][j] f[i][j] 表示走了 i i i次,第 i i i Arrive at the point after the walk j j j 的方案数
第 i i i The number of steps taken is ( k + i − 1 ) (k+i-1) (k+i−1) 的倍数
The template for a full backpack without restrictions is :
for (int i = 1; i <= n; ++i) f[i] = 0;
f[0] = 1;
for (int step = k; (start = (step + k) * (step - k + 1) / 2) <= n; ++step)
for (int j = 0; j <= n; ++j)
if (j >= step) f[i][j] += f[i - 1][j - step];
But this question is limited to :走第 i i i 次前,must have gone 1 1 1 到 i − 1 i-1 i−1次
Every time you need to force a walk i − 1 i-1 i−1 次,如下:
for (int i = 1; i <= n; ++i) f[0][i] = 0;
f[0][0] = 1;
for (int step = k; (step + k) * (step - k + 1) / 2 <= n; ++step) {
for (int j = 0; j <= n; ++j)
if (j >= step) f[i][j] = f[i - 1][j - step];
else f[i][j] = 0;
for (int j = 0; j <= n; ++j)
if (j >= step) f[i][j] += f[i - 1][j - step];
for (int j = 1; j <= n; ++j) ans[j] += f[j];
}
Optimize the scrolling array:
for (int i = 1; i <= n; ++i) f[i] = 0;
f[0] = 1;
for (int step = k; (step + k) * (step - k + 1) / 2 <= n; ++step) {
for (int j = n; j >= 0; --j)
if (j >= step) f[j] = f[j - step];
else f[j] = 0;
for (int j = 0; j <= n; ++j)
if (j >= step) f[j] += f[j - step];
for (int j = 1; j <= n; ++j) ans[j] += f[j];
}
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 200010;
const int mod = 998244353;
int dp[2][N];
int f[N];
int ans[N];
int n, k;
void add(int& a, int b) {
a += b;
if (a >= mod) a -= mod;
}
void solve() {
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; ++i) f[i] = 0;
f[0] = 1;
for (int step = k, start; (start = (step + k) * (step - k + 1) / 2) <= n; ++step) {
for (int j = n; j >= 0; --j)
if (j >= start) f[j] = f[j - step];
else f[j] = 0;
for (int j = start; j <= n; ++j)
if (j >= start) add(f[j], f[j - step]);
for (int j = 1; j <= n; ++j) add(ans[j], f[j]);
}
for (int i = 1; i <= n; ++i) printf("%d%c", ans[i], " \n"[i == n]);
}
int main()
{
int T = 1;
// scanf("%d", &T);
for (int i = 1; i <= T; ++i) {
solve();
}
return 0;
}
总结:
Avoid jumping thinking,After constructing the transition equation from the naive 2D state,Then optimize the space and time according to the actual situation
边栏推荐
猜你喜欢

企鹅电竞登录鉴权系统架构与核心数据热备容灾方案

ps提示由于程序错误Photoshop无法完成请求怎么办

能用有效的win7旗舰版激活密钥永久激活码大全(100%激活)

Chapter 02 - Let's Get Started(C#篇)
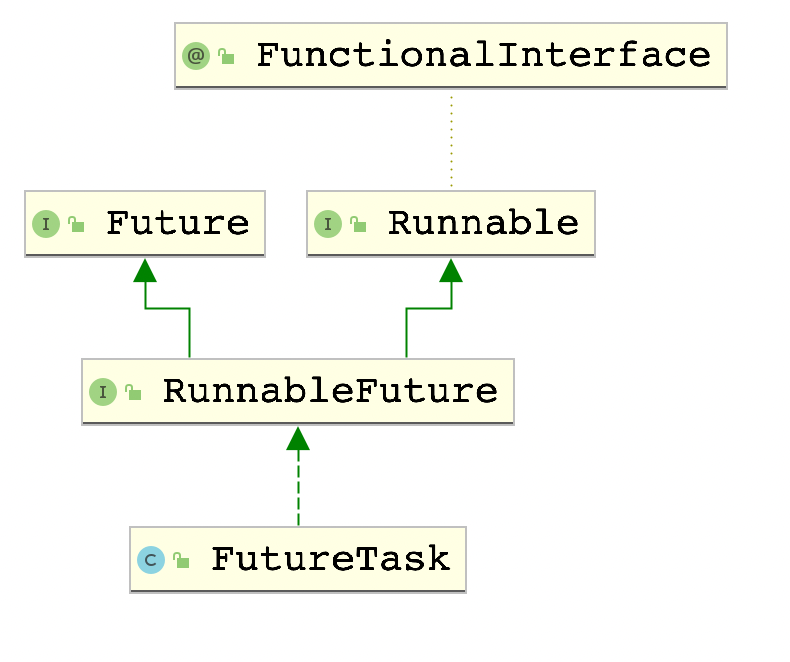
In-depth analysis of FutureTask source code

win7nvidia控制面板在哪 win7系统怎么打开nvidia控制面板

sudo相关漏洞CVE-2019-18634、CVE-2019-14287

startService启动服务,应用置于后台超过1min,服务被销毁

Chrome scroll bar style modification how to operate Chrome browser scroll bar style customization method

Concurrent programming essays necessary for interviews
随机推荐
手机注册股票开户安全吗是真的吗 开户要钱吗
EL expression
Win7怎么看硬盘大小 如何看电脑硬盘大小
TypeScript 开发环境搭建
redis无法远程连接的所有解决方案大全
服务主机:本地服务网络受限怎么办_服务主机本地系统网络受限的解决方法
数据分析面试(一)统计基础篇
What to do if the computer can't delete the folder
未解决的notebook问题
Win7系统添加韩文韩语输入法的方法
MySQL面试必备(四)锁篇
ELK日志平台搭建(一)
win7无法安装office2013怎么办 win7安装不了office2013如何处理
MySQL面试必备(三)事务篇
C语言——字符逆序( gets( )函数 )
startService启动服务,应用置于后台超过1min,服务被销毁
鼠标单击偶尔变双击了怎么办_电脑鼠标单击变双击了怎么设置
怎么能保护眼睛 电脑什么颜色保护眼睛
能用有效的win7旗舰版激活密钥永久激活码大全(100%激活)
cad字体库放在哪里 cad字体库在哪个文件夹