当前位置:网站首页>概率论基础 - 9 - 中心极限定理
概率论基础 - 9 - 中心极限定理
2022-08-05 14:31:00 【为为为什么】
中心极限定理(Central Limit Theorem,CTL),是指概率论中讨论随机变量序列部分和分布渐近于正态分布的一类定理。。
概述
定理是数理统计学和误差分析的理论基础,指出了大量随机变量近似服从正态分布的条件。它是概率论中最重要的一类定理,有广泛的实际应用背景。在自然界与生产中,一些现象受到许多相互独立的随机因素的影响,如果每个因素所产生的影响都很微小时,总的影响可以看作是服从正态分布的。中心极限定理就是从数学上证明了这一现象。 ——百度百科
- 中心极限定理(CLT)指出,如果样本量足够大,则变量均值的采样分布将近似于正态分布,而与该变量在总体中的分布无关。
独立同分布
- 设随机变量X_1, X_2,\dots,X_n独立同分布,且具有数学期望\mu和方差\sigma^2,前n个变量之和为\overline S = \sum\limits_{i = 1}^n {{X_i}} \\
- 那么\overline S_n的期望和方差为n\mu和n\sigma^2,\overline S_n的标准化变量为:
定义
- 中心极限定理的内容为:Y_n的概率分布函数F_n(x)对于任意x满足:
证明
通过观察某个分布的采样均值可以发现近似服从正态分布,我们的目标就是证明这个变量与正态分布的特征函数相同
- 引入一些特征函数的结论
- 正态分布的特征函数:
- 随机变量X_i的特征函数用{\varphi_x (t)}表示
- \overline S_n的特征函数为:
- X_i均值\overline X=\frac{1}{n}\overline {S_n}的特征函数:
- Y_n=\frac{\overline S_n - n\mu}{\sqrt n\sigma}=\frac{\overline X - \mu}{\frac{\sigma}{\sqrt n}}=\frac{\sqrt n}{\sigma}\overline X - \frac{\sqrt n}{\sigma} \mu 的特征函数:
思路1
- 取对数:
- 令p=\frac{t}{\sigma \sqrt{n}}, 当 n \rightarrow \infty 时, p \rightarrow 0 又 :
- 有 :
思路2
- \phi(t) 为 \eta_{i} 的特征函数
- \phi\left(\frac{t}{\sigma \sqrt{n}}\right) 在0点处的泰勒展开形式为:
- 所以, \varphi(t) 为:
都得出结论
- 即有:
- Y_n特征函数与正态分布相同,故有当 n \rightarrow \infty时,Y_n服从正态分布的结论
应用思路
- 均值方差为\mu和\sigma^2,的独立同分布的随机变量X_i前n项之和\overline S_n的标准变化量Y_n,当n充分大时,其分布近似于标准正态分布
- 即在n充分大时,\overline S_n分布近似于N(n\mu,n\sigma^2)
- 一般情况下,很难求出n个随机变量之和的分布函数。因此当n充分大时,可以通过正态分布来做理论上的分析或者计算
独立不同分布
- 相互独立, 具有数学期望和方差:
- 记: B_{n}{2}=\sum_{k=1}{n} \sigma_{k}^{2} 若存在正数 \delta, 使得当 n \rightarrow \infty 时,有:
- 则随机变量之和 \overline{S X_{n}}=\sum_{k=1}^{n} X_{k} 的标准变化量:
- 概率分布函数 F_{n}(x) 对于任意 x 满足:
- 其物理意义为: 相互独立的随机变量 X_{1}, X_{2}, \cdots, X_{n}, \cdots 之和 \overline{S X_{n}}=\sum_{k=1}^{n} X_{k} 的衍生随机变量序列 Z_{n}=\frac{\overline{S X_{n}}-\sum_{k=1}^{n} \mu_{k}}{B_{n}}, 当 n 充分大时, 其分布近似与标准正态分布。
- 这里并不要求 X_{1}, X_{2}, \cdots, X_{n}, \cdots 同分布。
棣莫佛-拉普拉斯定理
- Demoiver-Laplace 定理:设随机变量序列 \eta_{n}, n=1,2, \ldots 服从参数为 (n, p) 的二项分布,其中 0<p<1x, 有:
- 该定理表明, 正态分布是二项分布的极限分布。当 n 充分大时,可以利用正态分布来计算二项分布的概率。
参考资料
边栏推荐
- Thorns and Roses: The Road to Growth for Basic Service Architects PPT
- 灵活好用的sql monitoring 脚本 part2
- 基于STM32单片机设计指纹考勤机+上位机管理
- 拉格朗日乘数法
- vscode背景调整
- Get the order details of the purchased products on Taobao/Tmall——buyer_order_detail
- day14·私有化属性
- PaddleOCR User Guide
- 高效会议纪要重点
- HDD Hangzhou Station • ArkUI makes development more flexible
猜你喜欢

Integration testing of software testing

产品快讯 | 数字平台试用环境全新升级!欢迎咨询试用!

Rocket MQ Crash-Safe机制浅析
![[CUDA study notes] What is GPU computing](/img/20/6c68dbba66904b58a20c143c0f576d.png)
[CUDA study notes] What is GPU computing

Redis-浅谈主从同步

20款短视频自媒体必备工具,让你的运营效率翻倍
NLP 论文领读|无参数机器翻译遇上对比学习:效率和性能我全都要!
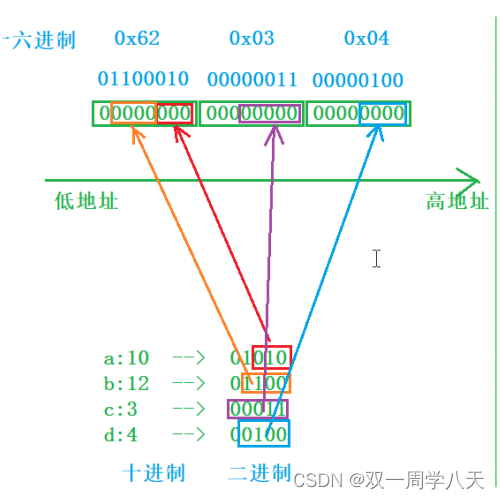
It is more detailed than a certain teacher (anti-PPT series) series - custom type (below)

神经网络的原理和应用,神经网络理论及应用

Design of Fingerprint Time Attendance Machine + Host Computer Management Based on STM32 MCU
随机推荐
荆棘与玫瑰:基础服务架构师的成⻓之路PPT
训练好的神经网络怎么用,神经网络训练电脑配置
Stuck at sill idealTree buildDeps when npm install
Observation cloud product update|DCA web terminal is online; new global viewer auto refresh configuration; new global blacklist function; new custom function menu, etc.
NLP paper reading | Parametric machine translation meets comparative learning: I want both efficiency and performance!
OpenHarmony如何查询设备类型
第五讲 测试技术与用例设计
day14·私有化属性
ソイラ / 索伊拉
背后的力量 | 开启智能化教学新体验 华云数据助力天长市工业学校打造新型IT实训室
PaddleOCR User Guide
Analysis of Rocket MQ Crash-Safe Mechanism
如何用一条命令将网页转成电脑 App
Today's sleep quality record 78 points
01.Gameplay Architecture ECS简介
抖音自媒体账号被限流?这3种方法教你如何鉴别
正交-不相关-独立
[WiFi] ebtable实现wifi接口之间数据隔离
软件测试之对测试平台的看法
ES6解构详解