当前位置:网站首页>[Pytorch] Study Notes (1)
[Pytorch] Study Notes (1)
2022-08-08 23:12:00 【swaying tree】
引言
课程视频链接:https://www.bilibili.com/video/BV1Y7411d7Ys?from=search&seid=17942018663670881374
The author thinks that speaks very easy to understand
1 线性模型
1.1 线性模型
y ^ = x ∗ w + b \hat y=x*w+b y^=x∗w+b
1.2 损失(针对单个样本)
l o s s = ( y ^ − y ) 2 = ( x ∗ w − y ) 2 loss = (\hat y-y)^2=(x*w-y)^2 loss=(y^−y)2=(x∗w−y)2
1.3 均方误差 MSE(In view of the training sample)
c o s t = 1 N ∑ n = 1 N ( y ^ n − y n ) 2 cost = \frac {1} {N}\sum_{n=1}^{N} {(\hat y_n-y_n)^2} cost=N1n=1∑N(y^n−yn)2
1.4 代码实现(用numpy)
import numpy as np
import matplotlib.pyplot as plt
# 数据集准备
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
def forward(x): # 定义线性模型
return x*w
def loss(x,y): # 定义损失函数(A single sample cost)
y_pred = forward(x)
return (y_pred - y)*(y_pred - y)
w_list = []
mse_list = []
for w in np.arange(0.0,4.1,0.1): # Exhaustive method list weight
print('w = ',w)
l_sum = 0
for x_val,y_val in zip(x_data,y_data):
y_pred_val = forward(x_val)
loss_val = loss(x_val,y_val)
l_sum+=loss_val
print('\t',x_val,y_val,y_pred_val,loss_val)
print('MSE=',l_sum/3)
w_list.append(w)
mse_list.append(l_sum/3)
# 绘图
plt.plot(w_list,mse_list)
plt.ylabel('loss')
plt.xlabel('w')
plt.show()
运行结果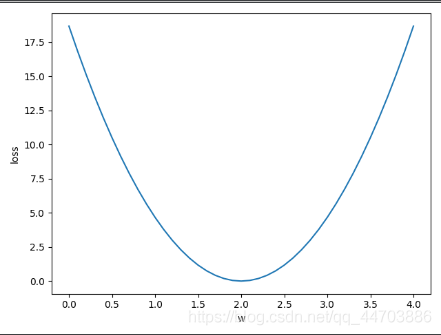
可视化训练过程(Visdom工具)
http://github.com/facebookresearch/visdom
matlab 3d图绘制
2 梯度下降
Search optimal weighting method(优化问题):
- 穷举法
- 分治法(Only for convex function,Otherwise can find local optimal)
- 梯度下降法(贪心)

梯度定义:
∂ c o s t ( w ) ∂ w = ∂ ∂ w 1 N ∑ n = 1 N ( y ^ n − y n ) 2 = 1 N ∑ n = 1 N ∂ ∂ w ( x n ⋅ w − y n ) 2 = 1 N ∑ n = 1 N 2 ⋅ ( x n ⋅ w − y n ) ∂ ( x n ⋅ w − y n ) ∂ w = 1 N ∑ n = 1 N 2 ⋅ x n ⋅ ( x n ⋅ w − y n ) \frac {\partial cost(w)} {\partial w} = \frac {\partial} {\partial w} \frac {1} {N} \sum_{n=1}^{N} {(\hat y_n-y_n)^2} \\= \frac {1} {N} \sum_{n=1}^{N}\frac {\partial} {\partial w} {(x_n\cdot w-y_n)^2} \\= \frac {1} {N} \sum_{n=1}^{N} 2\cdot{(x_n\cdot w-y_n)} \frac {\partial (x_n\cdot w-y_n)} {\partial w}\\= \frac {1} {N} \sum_{n=1}^{N} {2 \cdot x_n\cdot(x_n\cdot w-y_n)} ∂w∂cost(w)=∂w∂N1n=1∑N(y^n−yn)2=N1n=1∑N∂w∂(xn⋅w−yn)2=N1n=1∑N2⋅(xn⋅w−yn)∂w∂(xn⋅w−yn)=N1n=1∑N2⋅xn⋅(xn⋅w−yn)
2.1 梯度下降算法
w = w − ∂ c o s t ∂ w w=w- \frac {\partial cost} {\partial w} w=w−∂w∂cost
其中
∂ c o s t ∂ w = 1 N ∑ n = 1 N 2 ⋅ x n ⋅ ( x n ⋅ w − y n ) \frac {\partial cost} {\partial w} = \frac {1} {N} \sum_{n=1}^{N} {2 \cdot x_n\cdot(x_n\cdot w-y_n)} ∂w∂cost=N1n=1∑N2⋅xn⋅(xn⋅w−yn)
w = 1.0
def forward(x): # 线性模型
return x*w
def cost(xs,ys):
cost = 0
for x,y in zip(xs,ys):
y_pred = forward(x)
cost += (y_pred-y)**2
return cost/len(xs)
def gradient(xs,ys):
grad = 0
for x,y in zip(xs,ys):
grad += 2*x*(x*w-y)
return grad/len(xs)
print('Predict (before training)', 4, forward(4))
for epoch in range(100):
cost_val = cost(x_data,y_data)
grad_val = gradient(x_data,y_data)
w-=0.01*grad_val
print('Epoch:',epoch,'w=',w,'loss=',cost_val)
print('Predict (after training)',4,forward(4))
2.2 随机梯度下降
意义:Large sample when studying,With all the loss of the sample,计算量太大,训练太慢
w = w − ∂ l o s s ∂ w w=w- \frac {\partial loss} {\partial w} w=w−∂w∂loss
其中
∂ l o s s n ∂ w = 2 ⋅ x n ⋅ ( x n ⋅ w − y n ) \frac {\partial loss_n} {\partial w} =2 \cdot x_n\cdot(x_n\cdot w-y_n) ∂w∂lossn=2⋅xn⋅(xn⋅w−yn)

# 2.2 随机梯度下降
w = 1.0
def forward(x): # 线性模型
return x*w
def loss(x,y):
y_pred = forward(x)
return (y_pred-y)**2
def gradient(x,y):
return 2*x*(x*w-y)
print('Predict (before training)', 4, forward(4))
for epoch in range(100):
for x,y in zip(x_data,y_data):
grad = gradient(x_data,y_data)
w = w-0.01*grad
print('\tgrad:',x,y,grad)
l = loss(x,y)
print('progress:',epoch,'w=',w,'loss',l)
print('Predict (after training)',4,forward(4))
Comprehensive the above two kinds of gradient descent algorithm,By far the most commonly used bulk stochastic gradient descent(Mini_Batch)
3 反向传播算法
3.1 Weight updating calculation
w = w − ∂ c o s t ∂ w w=w- \frac {\partial cost} {\partial w} w=w−∂w∂cost
权重的维度:输出维度*输入维度
The significance of nonlinear activation
线性变换,No matter how many layers increase,Eventually linear mode,Add layers become meaningless.

In order to improve the complexity of the model,In each layer of the final output of linear increase a nonlinear transformation function(激活函数).
3.2 链式求导法则

Back propagation sample: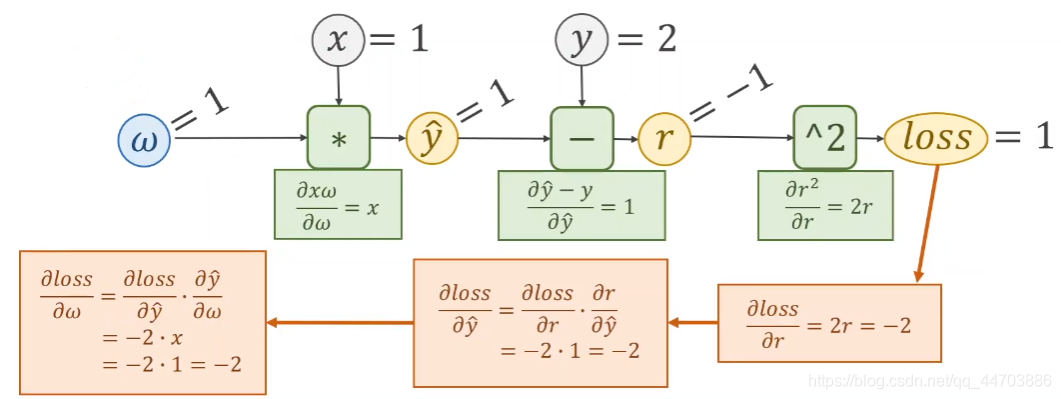
3.3 pytorch实现反向传播
在pytorchTensor contains the weight value and the loss in weight of derivative
import torch
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
w = torch.Tensor([1.0]) # 张量
w.requires_grad = True # 需要计算梯度
# As long as the containing tensor,Definition of the function is no longer a simple calculation,But to build calculation chart
def forward(x):
return x*w
def loss(x,y):
y_pred = forward(x)
return (y_pred-y)**2
# 训练
print('predict(before training)',4,forward(4).item())
for epoch in range(100):
for x,y in zip(x_data,y_data):
l = loss(x,y) # 张量
l.backward() # 反向传播,Automatic enduresw,At the same time calculation chart release
print('\tgrad:',x,y,w.grad.item())
w.data = w.data - 0.01*w.grad.data # 权重更新
w.grad.data.zero_() # 梯度清零
print('progress:',epoch,l.item())
print('predict(after training)',4,forward(4).item())
边栏推荐
- JSDay2-两个数组的交集
- A preliminary study on the use of ndk and JNI
- Hi3516 使用 wifi模块
- 【Bug解决】ValueError: Object arrays cannot be loaded when allow_pickle=False
- Tp5 in cache cache, storage cell phone text message authentication code
- [Bug solution] ValueError: Object arrays cannot be loaded when allow_pickle=False
- 小程序banner图展示
- 微信小程序错误 undefined Expecting ‘STRING‘,‘NUMBER‘,‘NULL‘,‘TRUE‘,‘FALSE‘,‘{‘,‘[‘, got ]解决方案
- 2022牛客多校六 M-Z-Game on grid(动态规划)
- Hi3516 use wifi module
猜你喜欢

使用Mongoose populate实现多表关联存储与查询,内附完整代码

(newcoder 15079)无关(容斥原理)

2022杭电多校六 1007-Shinobu loves trip(同余方程)

(2022牛客多校五)G-KFC Crazy Thursday(二分+哈希/Manacher)

最详树莓派4B装机流程及ifconfig不到wlan0的解决办法
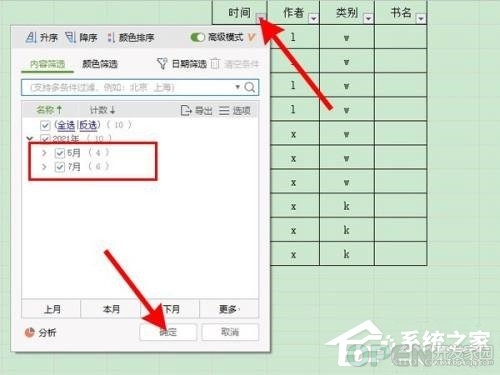
wps表格怎么筛选出需要的内容?wps表格筛选出需要的内容的方法

2022牛客多校六 M-Z-Game on grid(动态规划)

用模态框 实现 注册 登陆

二叉树 层次遍历 及例题
![微信小程序错误 undefined Expecting ‘STRING‘,‘NUMBER‘,‘NULL‘,‘TRUE‘,‘FALSE‘,‘{‘,‘[‘, got ]解决方案](/img/31/a9b0c31f648d41e300949ac43c5cab.png)
微信小程序错误 undefined Expecting ‘STRING‘,‘NUMBER‘,‘NULL‘,‘TRUE‘,‘FALSE‘,‘{‘,‘[‘, got ]解决方案
随机推荐
【PP-YOLOv2】训练自定义的数据集
Kubernetes 资源核心原理
Kubernetes与OpenStack
Dynamic Host Configuration Protocol DHCP (DHCPv4)
2022杭电多校五 C - Slipper (dijkstra+虚拟结点)
Kubernetes与OpenStack
MySQL indexes a field in a table
Button Wizard for ts API usage
容斥原理
【YOLOv5】6.0环境搭建(不定时更新)
用工具实现 Mock API 的整个流程
动手写prometheus的exporter-01-Gauge(仪表盘)
(2022杭电多校四)1011-Link is as bear(思维+线性基)
WeChat applet wx:for loop output example
WeChat small program "decompiled" combat "behind to unpack the eggs
sess.restore() 和 tf.import_meta_graph() 在使用时的一些关联
Analysis of WLAN - Wireless Local Area Network
(newcoder 15079)无关(容斥原理)
树莓派wiringPi库的使用补充
有了国产 DevOps 工具 ,还怕数字化转型成本高?