当前位置:网站首页>取模运算(MOD)
取模运算(MOD)
2022-08-04 00:15:00 【super阿真】
目录
一、基本的运算律

二、消去律
定理(消去律):如果gcd(c,p) = 1 ,则 ac ≡ bc mod p 可以推出 a ≡ (b mod p)
三、欧拉函数
欧拉函数是数论中很重要的一个函数,欧拉函数是指:对于一个正整数n,小于n且和n互质的正整数的个数,记做:φ(n),其中φ(1)被定义为1,但是并没有任何实质的意义。
定义小于n且和n互质的数构成的集合为Zn,称呼这个集合为n的完全余数集合。
显然,对于素数p,φ(p)= p -1.对于两个素数p、q,他们的乘积n = pq 满足φ(n) =(p-1)(q-1)
证明:对于质数p,q,满足φ(n) =(p-1)(q-1)
考虑n的完全余数集Zn = { 1,2,....,pq -1},而不和n互质的集合由下面三个集合的并构成:
1) 能够被p整除的集合{p,2p,3p,....,(q-1)p} 共计q-1个
2) 能够被q整除的集合{q,2q,3q,....,(p-1)q} 共计p-1个
3)很显然,1、2集合中没有共同的元素,因此Zn中元素个数 = pq - (p-1 + q- 1 + 1) = (p-1)(q-1)
四、欧拉定理
![]()
五、 参考
边栏推荐
猜你喜欢

通过whl安装第三方包

JVM垃圾回收总结(未完待续)

学习笔记 | uiautomation(如何)实现自动化

Nanoprobes丨Nanogold-抗体和链霉亲和素偶联物

【面经】被虐了之后,我翻烂了equals源码,总结如下

求解同余方程 数论 扩展欧几里得

The world's first mass production, with the most fixed points!How does this AVP Tier1 lead?

win10+cuda11.7+pytorch1.12.0 installation

孙宇晨受邀参加36氪元宇宙峰会并发表主题演讲
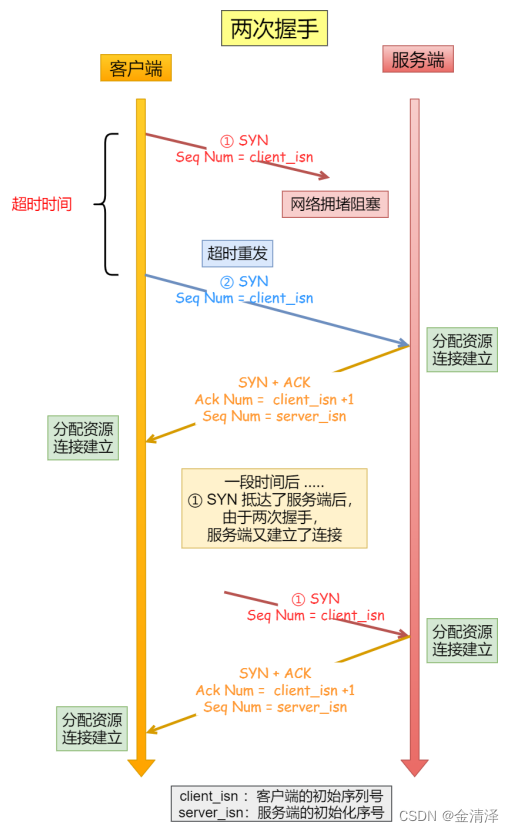
A simple understanding of TCP, learn how to shake hands, wave hands and various states
随机推荐
boot issue
2015年开源大事件汇总
JVM垃圾回收总结(未完待续)
机器学习——库
C语言实验十四 结构体
Apple told Qualcomm: I bought a new campus for $445 million and may plan to speed up self-development of baseband chips
Nanoprobes Alexa Fluor 488 FluoroNanogold 偶联物
建木DevOps流程的快速运用
免费的公共WiFi不要乱连,遭中间人攻击了吧?
七夕活动浪漫上线,别让网络拖慢和小姐姐的开黑时间
ping数据包中的进程号
小身材有大作用——光模块寿命分析(二)
It will invest about 200 billion US dollars in the United States in 20 years, and Samsung Electronics looks so handsome
A simple understanding of TCP, learn how to shake hands, wave hands and various states
【杂项】如何将指定字体装入电脑然后能在Office软件里使用该字体?
学习笔记 | uiautomation(如何)实现自动化
Salesforce's China business may see new changes, rumors may be closing
RSS订阅微信公众号初探-feed43
Spinnaker调用Jenkins API 返回403错误
超级完美版布局有快捷键,有背景置换