当前位置:网站首页>【数字信号处理】相关系数 ( 相关系数概念解析 | 信号能量常数 | 共轭序列 | 序列在相同时刻的相关性 )
【数字信号处理】相关系数 ( 相关系数概念解析 | 信号能量常数 | 共轭序列 | 序列在相同时刻的相关性 )
2022-04-21 13:07:00 【韩曙亮_】
文章目录
- 一、相关系数概念
- 二、相关系数概念解析
- 1、信号能量常数
- 2、共轭序列
- 3、序列在相同时刻的相关性
一、相关系数概念
" 相关系数 " 英文名称是 " Correlation Coefficient " ;
相关系数 , 就是一个数 , 如下表述 :
假设 x ( n ) x(n) x(n) 和 y ( n ) y(n) y(n) 是两个 能量有限 的 确定性信号 , 并且这 2 2 2 个序列 具有 因果性 , 则相关系数是 :
ρ x y = ∑ n = 0 ∞ x ( n ) y ∗ ( n ) [ ∑ n = 0 ∞ ∣ x ( n ) ∣ 2 ∑ n = 0 ∞ ∣ y ( n ) ∣ 2 ] 1 / 2 \rho_{xy} = \cfrac{\sum\limits_{n=0}^{\infty}x(n)y^*(n)}{ \Bigg[\sum\limits_{n=0}^{\infty} |x(n)|^2 \sum\limits_{n=0}^{\infty} |y(n)|^2 \Bigg]^{1/2} } ρxy=[n=0∑∞∣x(n)∣2n=0∑∞∣y(n)∣2]1/2n=0∑∞x(n)y∗(n)
ρ x y \rho_{xy} ρxy 就是 x ( n ) x(n) x(n) 和 y ( n ) y(n) y(n) 的 相关系数 ;
二、相关系数概念解析
1、信号能量常数
∑ n = 0 ∞ ∣ x ( n ) ∣ 2 \sum\limits_{n=0}^{\infty} |x(n)|^2 n=0∑∞∣x(n)∣2 和 ∑ n = 0 ∞ ∣ y ( n ) ∣ 2 \sum\limits_{n=0}^{\infty} |y(n)|^2 n=0∑∞∣y(n)∣2 是 信号的能量 , 两个序列都是能量有限的信号 , 其能量是固定的 , 这两个值也就是固定的常数值 ,
因此 ∑ n = 0 ∞ ∣ x ( n ) ∣ 2 ∑ n = 0 ∞ ∣ y ( n ) ∣ 2 \sum\limits_{n=0}^{\infty} |x(n)|^2 \sum\limits_{n=0}^{\infty} |y(n)|^2 n=0∑∞∣x(n)∣2n=0∑∞∣y(n)∣2 是一个常数 ;
2、共轭序列
共轭说明 :
数字信号处理 中 , 信号 是 复数 , 数字化之后 , 经过 数字下变频 , 输出的就是 复信号 , 因此这里使用 共轭 ;
信号与系统 中 , 信号 是 实数 , AD 采样之后是一个实信号 ;
3、序列在相同时刻的相关性
相关系数 ρ x y \rho_{xy} ρxy 主要取决于 分子中的 ∑ n = 0 ∞ x ( n ) y ∗ ( n ) \sum\limits_{n=0}^{\infty}x(n)y^*(n) n=0∑∞x(n)y∗(n) , 其中 y ∗ ( n ) y^*(n) y∗(n) 是 y ( n ) y(n) y(n) 的 共轭序列 ,
其 物理含义 是 x ( n ) , y ∗ ( n ) x(n) , y^*(n) x(n),y∗(n) 这两个信号 , 在相同的时刻 的 相关性 ;
如果 x ( n ) = y ( n ) x(n) = y(n) x(n)=y(n) 则 相关系数 ρ x y = 1 \rho_{xy} = 1 ρxy=1 ,
如果 x ( n ) ≠ y ( n ) x(n) \not= y(n) x(n)=y(n) 则 相关系数 ρ x y \rho_{xy} ρxy 取值在 [ 0 , 1 ) [0 , 1) [0,1) 区间内 ;
版权声明
本文为[韩曙亮_]所创,转载请带上原文链接,感谢
https://blog.51cto.com/u_14202100/5237063
边栏推荐
- Village vlog harvest 8000w + play, another flow ceiling?
- Repairing tables with SQL statements
- Shell programming learning (II) variables and operations
- In depth analysis of focal loss loss function
- 乡村vlog收割8000w+播放,又一个流量天花板?
- How to use mind map and flowchart for free (draw.io vs code integration)
- Filter 过滤器和 Listener 监听器
- Is the securities account opened by caibang safe? Or is it safer to open in securities companies?
- Call for Papers | IEEE/IAPR IJCB 2022 会议
- Revit secondary development - multi pipe linear annotation (phase 18)
猜你喜欢

redis数据持久化

(recommended intensive reading) this refers to the north

Meichuang technology was invited to carry out data security training for Haidian District academy of Educational Sciences

乡村vlog收割8000w+播放,又一个流量天花板?
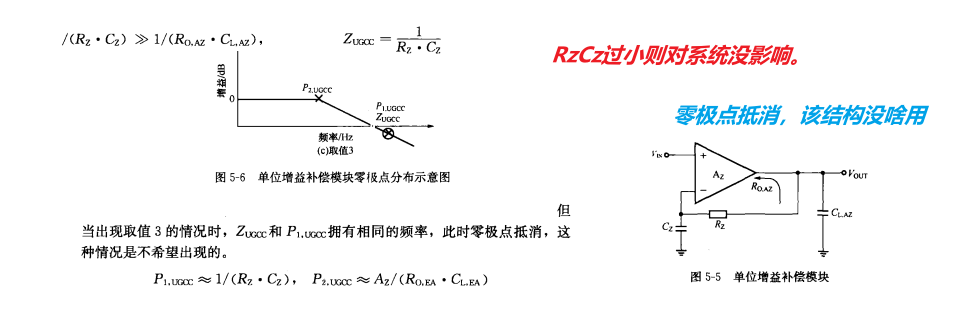
S:单位增益补偿

Qfileinfo file and folder operations

In depth analysis of focal loss loss function

美创科技受邀为海淀区教育科学研究院开展数据安全培训

Simulated Login of selenium's slider verification code (pig Bajie website)

Filter 过滤器和 Listener 监听器
随机推荐
Village vlog harvest 8000w + play, another flow ceiling?
Build a service registration and Discovery Center
斐波那契数列
CEPH practice (I) - Introduction to distributed storage and overview of its principle and architecture
CPT 102_LEC 10
With monthly sales exceeding 10 million, how can "Jiaoxia" become a popular manufacturing machine in the new sunscreen era?
In depth analysis of focal loss loss function
IEEE PR for paper | 202b
Convert m3u8 format to MP4 through fmpeg
Revit二次开发之——lookup的使用方法(第七期)
网易云---手机验证码登录
乡村vlog收割8000w+播放,又一个流量天花板?
Revit secondary development - creating walls (2) (phase 11)
(recommended intensive reading) this refers to the north
Revit二次开发——创建和切换标记(第十六期)
界面高级实战(未完)
Mysql database operation statement exercise
Sliding window series - find minimum overlay string
Revit二次开发之创建宿主元素(门窗等)(第十四期)
GSMA宣布:2022 MWC上海延期举办