当前位置:网站首页>P1446 [HNOI2008]Cards(Burnside定理+dp计数)
P1446 [HNOI2008]Cards(Burnside定理+dp计数)
2022-04-23 06:21:00 【Zimba_】
题意:
要给一副牌染色,染成 S r S_{r} Sr张红色, S b S_{b} Sb张蓝色, S g S_{g} Sg张绿色。现给出了 m m m种洗牌法(置换),当一副牌可以通过这 m m m种洗牌法 (可以用多种洗法,每种可以用多次)洗成另一副牌时,则称这两副牌是同一种。问能染出多少种不同副牌。
m a x { S r , S b , S g } ≤ 20 , m ≤ 60 max\{S_{r},S_{b},S_{g}\}\leq20,m\leq60 max{
Sr,Sb,Sg}≤20,m≤60
思路:
显然是 B u r n s i d e Burnside Burnside定理的运用(会不会用是另一回事)。
公式:
N ( G , C ) = 1 ∣ G ∣ ∑ f ∈ G C ( f ) N(G,C)=\frac{1}{|G|}\sum_{f\in G}C(f) N(G,C)=∣G∣1f∈G∑C(f)简单 介绍一下这个公式, G G G是置换群, C C C是着色集, C ( f ) C(f) C(f)是置换 f f f在着色集 C C C下的不动点数。
至于置换群要符合的要求,不是很懂。
这里的话, G G G里面的是,单位置换和 m m m种洗牌置换。着色集就是满足数量的三种颜色的所有不同排列。
我们考虑统计某个置换的不动点数。
然后会发现,一种着色在某个置换下不动,当前仅当每个循环节中的颜色相同。所以,我们对于每个置换,求出它的循环节,然后用 d p dp dp计数就可以了。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int Sr,Sb,Sg,m,p;
int n;
int a[105];
int flag[105];
int dp[30][30][30];
int getC()
{
memset(flag,0,sizeof(flag));
memset(dp,0,sizeof(dp));
dp[0][0][0]=1;
for(int i=1;i<=n;i++)if(!flag[i])
{
int now=i;
flag[now]=1;
int num=1;
while(!flag[a[now]])
{
num++;
now=a[now];
flag[now]=1;
}
for(int r=Sr;r>=0;r--)
{
for(int b=Sb;b>=0;b--)
{
for(int g=Sg;g>=0;g--)
{
if(r>=num)dp[r][b][g]=(dp[r][b][g]+dp[r-num][b][g])%p;
if(b>=num)dp[r][b][g]=(dp[r][b][g]+dp[r][b-num][g])%p;
if(g>=num)dp[r][b][g]=(dp[r][b][g]+dp[r][b][g-num])%p;
}
}
}
}
return dp[Sr][Sb][Sg];
}
int fpow(int a,int n,int p)
{
int sum=1,base=a;
while(n!=0)
{
if(n%2)sum=sum*base%p;
base=base*base%p;
n/=2;
}
return sum;
}
int main()
{
scanf("%d%d%d%d%d",&Sr,&Sb,&Sg,&m,&p);
n=Sr+Sb+Sg;
int ans=0;
for(int i=1;i<=n;i++)a[i]=i;
ans=(ans+getC())%p;
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)scanf("%d",&a[j]);
ans=(ans+getC())%p;
}
printf("%d\n",ans*fpow(m+1,p-2,p)%p);
return 0;
}
版权声明
本文为[Zimba_]所创,转载请带上原文链接,感谢
https://blog.csdn.net/weixin_43785386/article/details/108197481
边栏推荐
- MVCC(多版本并发控制)
- Background management system framework, there is always what you want
- [COCI]Lampice (二分+树分治+字符串哈希)
- SQL练习第一题
- How does the public and Private Integrated walkie talkie realize cooperative work under multi-mode communication?
- 后台管理系统框架,总有你想要的
- USO technology was invited to share the technical framework and challenges of AI synthetic virtual characters at lvson2020 conference
- Solution of emergency communication system for major security incidents
- 字节数仓实习生面试sql题
- 自定义classloader并实现热部署-使用loadClass
猜你喜欢

简单易懂的子集dp

How does the public and Private Integrated walkie talkie realize cooperative work under multi-mode communication?
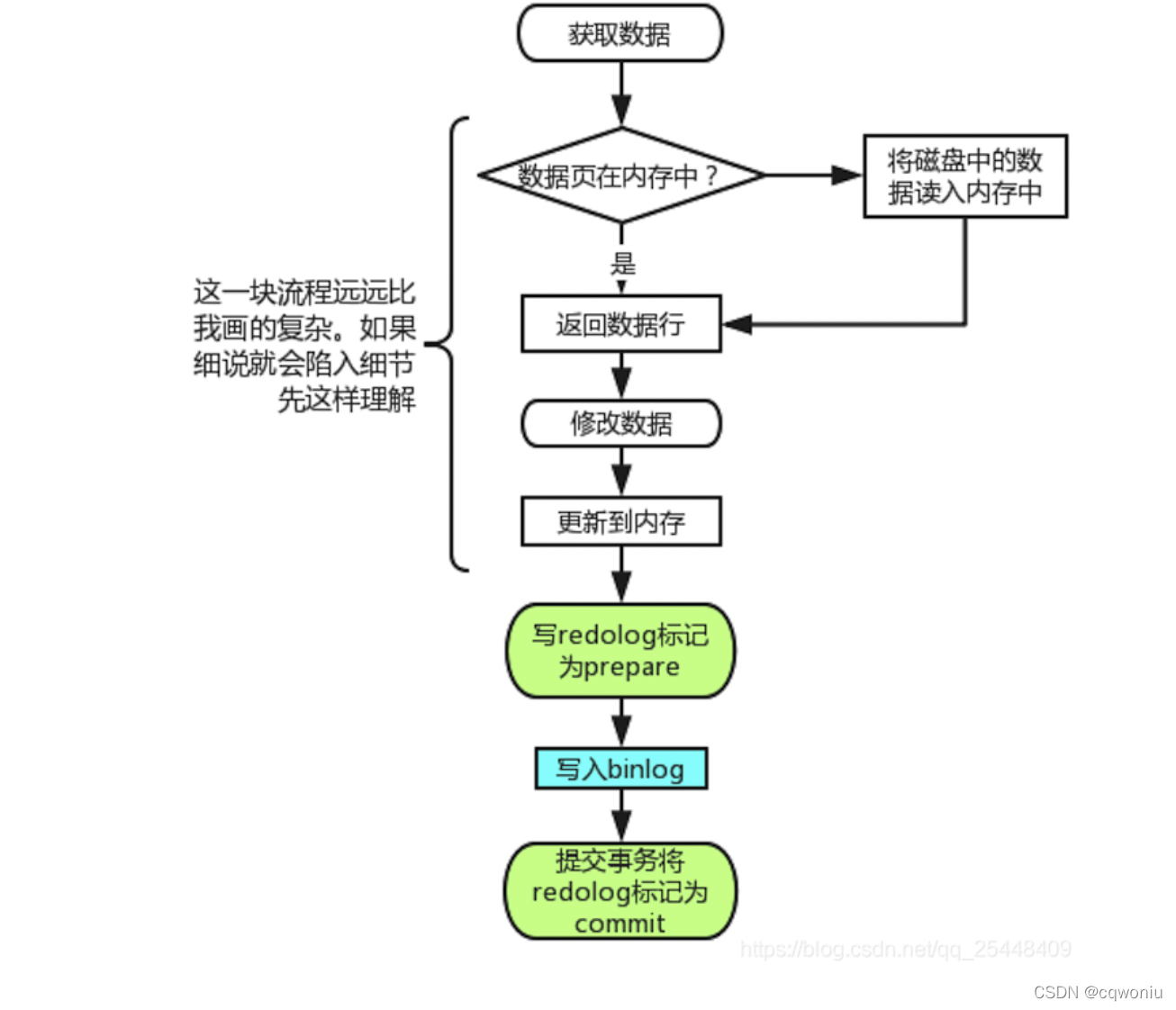
Mysql持久性的实现

Typora操作技巧说明(一).md

利用mysql-binlog恢复数据

DMR system solution of Kaiyuan MINGTING hotel of Fengqiao University
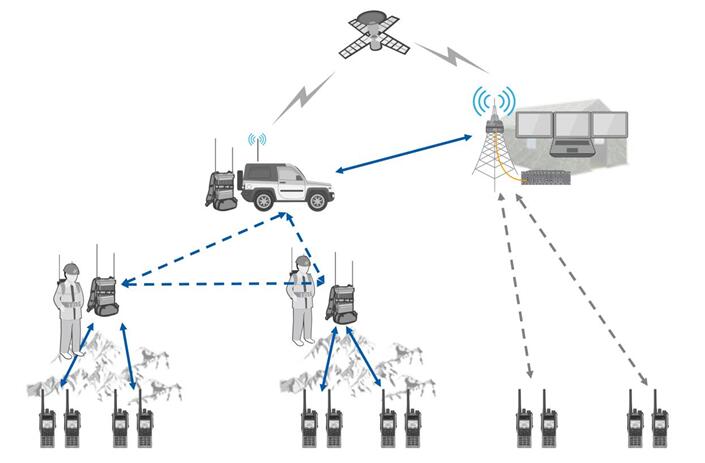
Flexible blind patch of ad hoc network | Beifeng oil and gas field survey solution

The people of Beifeng have been taking action
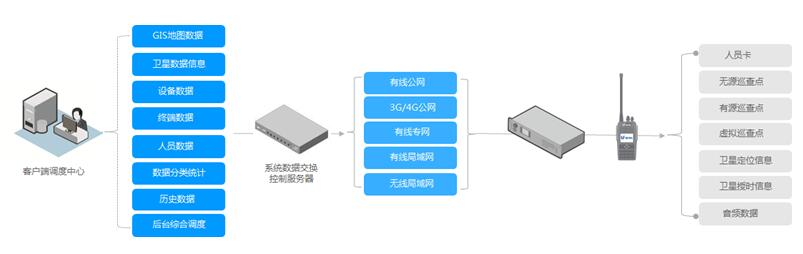
南方投资大厦SDC智能通信巡更管理系统

jvm知识点汇总-持续更新
随机推荐
Patrol inspection intercom communication system in power industry
Meishe technology launches professional video editing solution for desktop -- Meiying PC version
记录阿里云服务器挖矿程序处理
[COCI]Lampice (二分+树分治+字符串哈希)
免费开源智能充电桩物联网SAAS云平台
How to improve the service efficiency of the hotel without blind spots and long endurance | public and Private Integrated walkie talkie?
基于可视化结构的身份证号码校验系统-树莓派实现
Jupyter Notebook 安装
Meishe helps Baidu "Duka editing" to make knowledge creation easier
不需要破解markdown编辑工具Typora
学习资料
Pycharm
推导式与正则式
自定义钉钉机器人进行报警
可视化之路(九)Arrow类详解
记录一下使用v-print中遇到的问题
MVCC(多版本并发控制)
Beifeng communication helps Zhanjiang fire brigade build PDT wireless communication system
Background management system framework, there is always what you want
可视化常见问题解决方案(九)背景颜色问题