一、什么是delta方法

众所周知,当一个变量$X$服从正态分布时,Its linear transformation also obeys the normal distribution.What about nonlinear transformations?？

delta方法提出,It is obtained by transforming the differentiable function$g(X)$Still the probability tends to be normally distributed,and provides expectations、方差的计算公式.

单变量$X$ 变换为 $g(X)$,对$g(X)$泰勒展开：
$g(X)\approx g(\theta )+g^{\prime }(\theta )(X-\theta )$
$g(X)-g(\theta )\approx g^{\prime }(\theta )(X-\theta )\stackrel{\nu }{\to }N(0,{\sigma }^2\ast [g’(\theta ){]}^2)$

$g(\theta )$为常数,故$g(X)\to N(0,{\sigma }^2\ast [g^{\prime }(\theta ){]}^2)$

Multivariate transformation can also get the expectation and variance of the distribution,Often used to calculate the quotient of two random variables$\frac{Y}{X}$The distribution and the variance

$E(\frac{Y}{X})=\frac{E(Y)}{E(X)}$
$var(\frac{Y}{X})=\frac{var(X)}{Y^2}+\frac{X^{2}var(Y)}{Y^4}-2\frac{Xcov(X,Y)}{Y^3}$

二、应用背景

AB测试中的Randomized shunt unit（Randomization Unit）和指标的分析单元（Analysis Unit） 不同时.Central limit theorem requirements between the sample points are independent.ABThe triage unit in the experiment is the user,user-to-user independence.

• “人均”The analytical unit of the type indicator is the user,The value of each user is$X_1$,$X_2$,$X_3$…互相独立,此时$\bar{X}$可以用$z$检验.
• The unit of analysis for click-through rate is“每次曝光”,That is, averaging over the number of impressions,The sample point is$X_{11}$,$X_{12}$,$X_{13}$…,$X_{ij}$can be regarded as the first$i$个用户第$j$Whether or not to click on a second impression,Multiple exposures are not independent of each other,无法用$z$检验.

解决方法：Divided by the number of molecules in the denominator at the same time$n$,使用delta检验,得到$\overline{ctr}$服从正态分布,and the mean and variance can be obtained.Calculating variance requires per capita hits/Mean and variance of exposure per capita、and the covariance of clicks per capita and impressions per capita.

and then calculate the statistics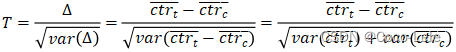

参考文献

https://www.jianshu.com/p/917dc1584452
https://toutiao.io/posts/q660w08/preview