Linear regression is generally used for data prediction,The predicted results are generally real numbers.
Logistic regression is generally used for classification prediction,The prediction results are generally some kind of probabilities.

线性回归

Step 1: Model

定义模型

Step 2: Goodness of Function

定义 Loss 函数,Used to judge whether the model is good or bad,selected here MSE

通过最小化 Loss 函数,来得到更好的模型

Step 3: Gradient Descent

Parameters are optimized by gradient descent

Gradient descent with two parameters

可视化

Linear regression There is no local optimal solution

分别对 $w$ 和 $b$ 求偏导

How’s the results?

Model Selection

Introduce multiple items,定义更复杂的 Model

It may appear when the model is more complex Overfitting 的情况

Back to step 1: Redesign the Model

重新定义模型,Consider the effect of species on the results

考虑其他 feature 对结果的影响,重新定义Model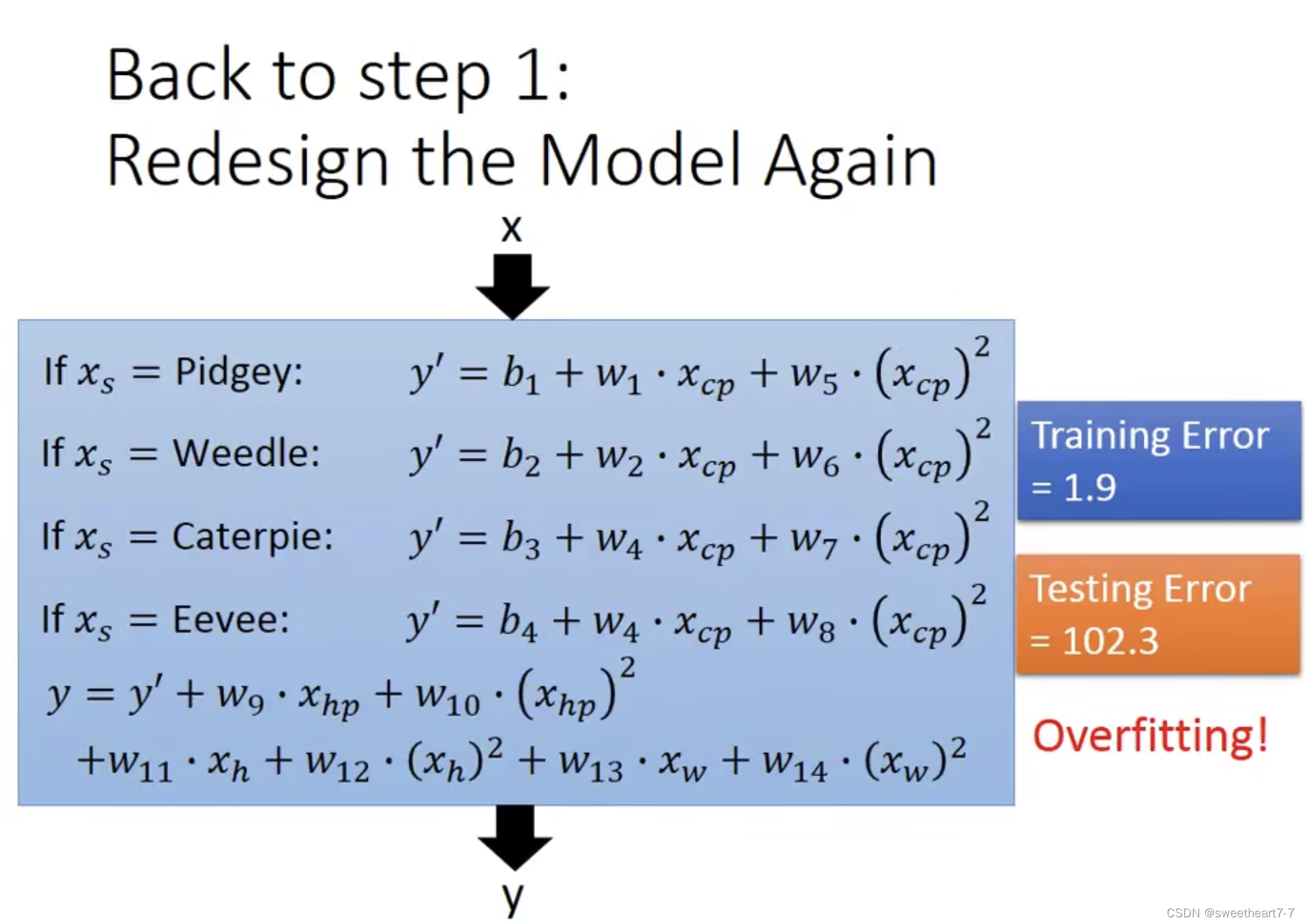

Back top step 2: Regularization

对 Loss function 加入 正则化来解决 Overfitting 问题

Regularization

正则化：Expect smaller parameters function,越平滑,output 对输入的变化是比较不敏感的,Can be insensitive to noise.

λ The bigger the description, the more consideration $w$ 本身大小,And the less you think about yourself Loss 大小,所以在 training data performance is getting worse.

为什么不考虑 $b$,Because what we need is a smooth one function,而 $b$ 的大小不会改变 function 的平滑程度.

逻辑回归

Ideally define the model function for the classification task

Solved by Gaussian distribution

The data is assumed to belong to a Gaussian distribution（Other distributions can also be assumed,There are subjective conscious influences here）,The problem is then solved by a Gaussian model.

Generative Model

最大化 Likelihood

求出 μ 和 ∑

used allfeature ,The result was still broken

Consider giving twoModel 公用 covariance matrix,这样就只需要较少的 parameters（不容易 overfitting）

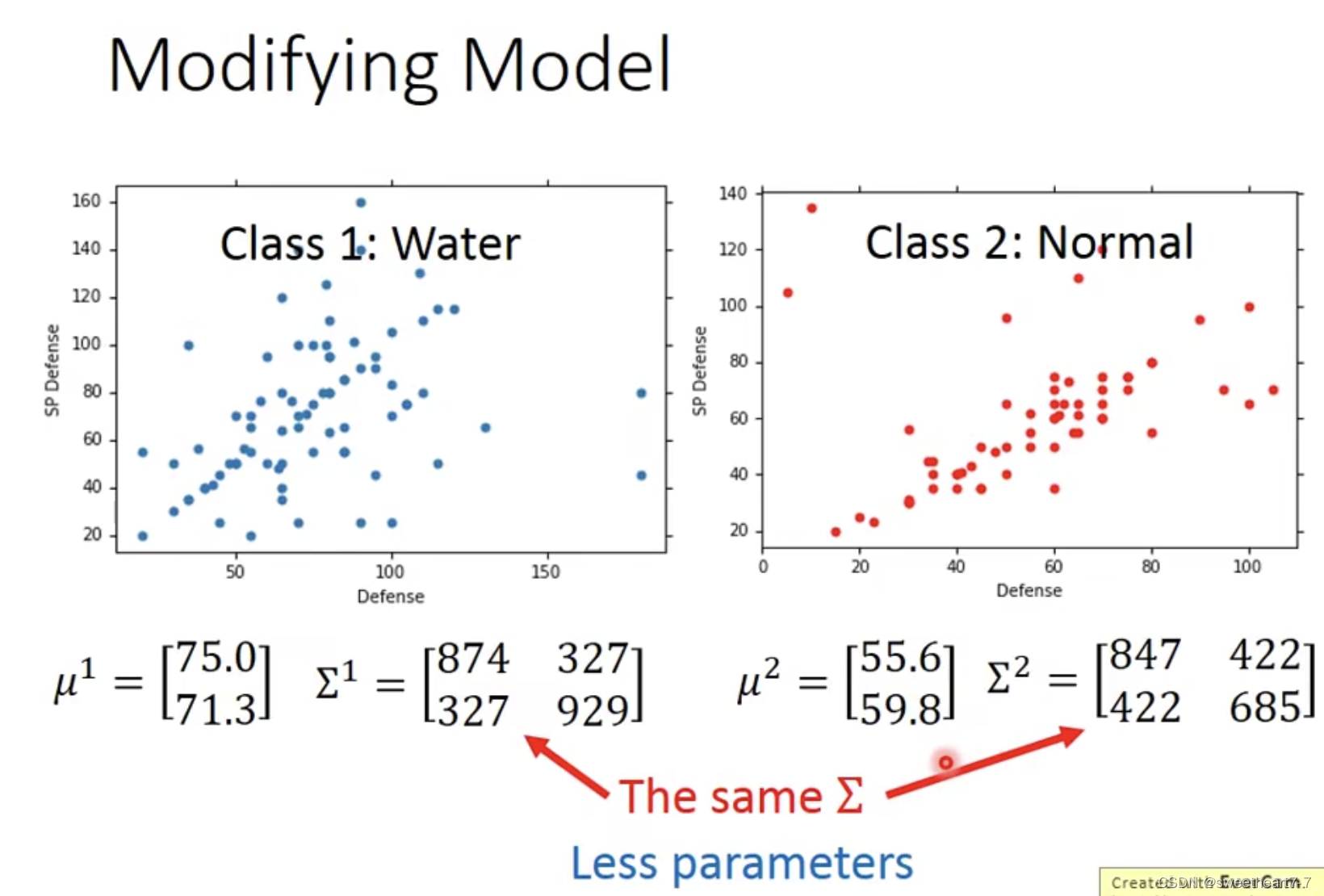
求出 μ 和 ∑

found public ∑ 后,此时的 boundary 是线性的,The accuracy rate has improved a lot.

Three Steps

So the summary is as follows 3 步：

Naive Bayes Classifier

假设所有的 feture 是 independent,Its probability can be expressed in the following form,This model belongs to Naive Bayes Classifier

Posterior Probility

分析 Posterior Probability

Discovered by formula derivation：It can eventually also be written as $\sigma (w\ast x+b)$

Step 1: Function Set

推出来的 σ 就是 sigmoid 函数,其图像表示如下：

It can be represented in the form as follows：

Step 2: Goodness of a Function

最大化 Likelihood 就是最小化 $-lnL(w,b)$,Expand as follows：

这种 Loss 函数就是 cross entropy The meaning of representation is two distribution 有多接近,越小越接近

Step 3: Find the best function

$w$ 的 update Depends on three things：

1. learning rate
2. $x_i$ 来自于 data
3. $\hat{y}-f(x^n)$,代表 f 的 output 与 理想的 目标值$\hat{y}$差距有多大,离目标越远,update the larger the amount

Why can't logistic regression be used MSE 作为 Loss 函数？

• 当 $\hat{y}=1$ 时,If the predicted result is $f(x)=0$,At this time, it is clearly far from the target value,But the gradient value at this time is $0$！
• 当 $\hat{y}=0$ 时,If the predicted result is $f(x)=1$,At this time, it is clearly far from the target value,But the gradient value at this time is $0$！

Cross Entropy vs Square Error

If the logistic regression problem is used square error 时,The gradient may appear in the distance 0 的情况,而不能更新.

Discriminative vs Generative

Discriminative Model Just define the function directly,Then optimize the function Model,Let the machine find it by itself distribution.
Generative Model is to assume one first distribution,Then find the parameter value (μ 和 ∑) 带入 Model.

Accuracy varies

Generative Model made some assumptions

举例：

Used in this example Generative Model 得到 data1 probability is less than 0.5（因为 Navie Bayes Model 假设两个 feature 独立）

在 training data 少的时候,Generative Model 可能表现更好,Not easily affected by noise.

Multi-class Classification

Multi-classification can be solved with the following model
softmax 也可以通过 Gaussain Model 推导出来

多分类问题 Loss 函数 也可以用 Cross Entropy 定义

Limitation of Logistic Regression

The following situation is difficult to solve with logistic regression.

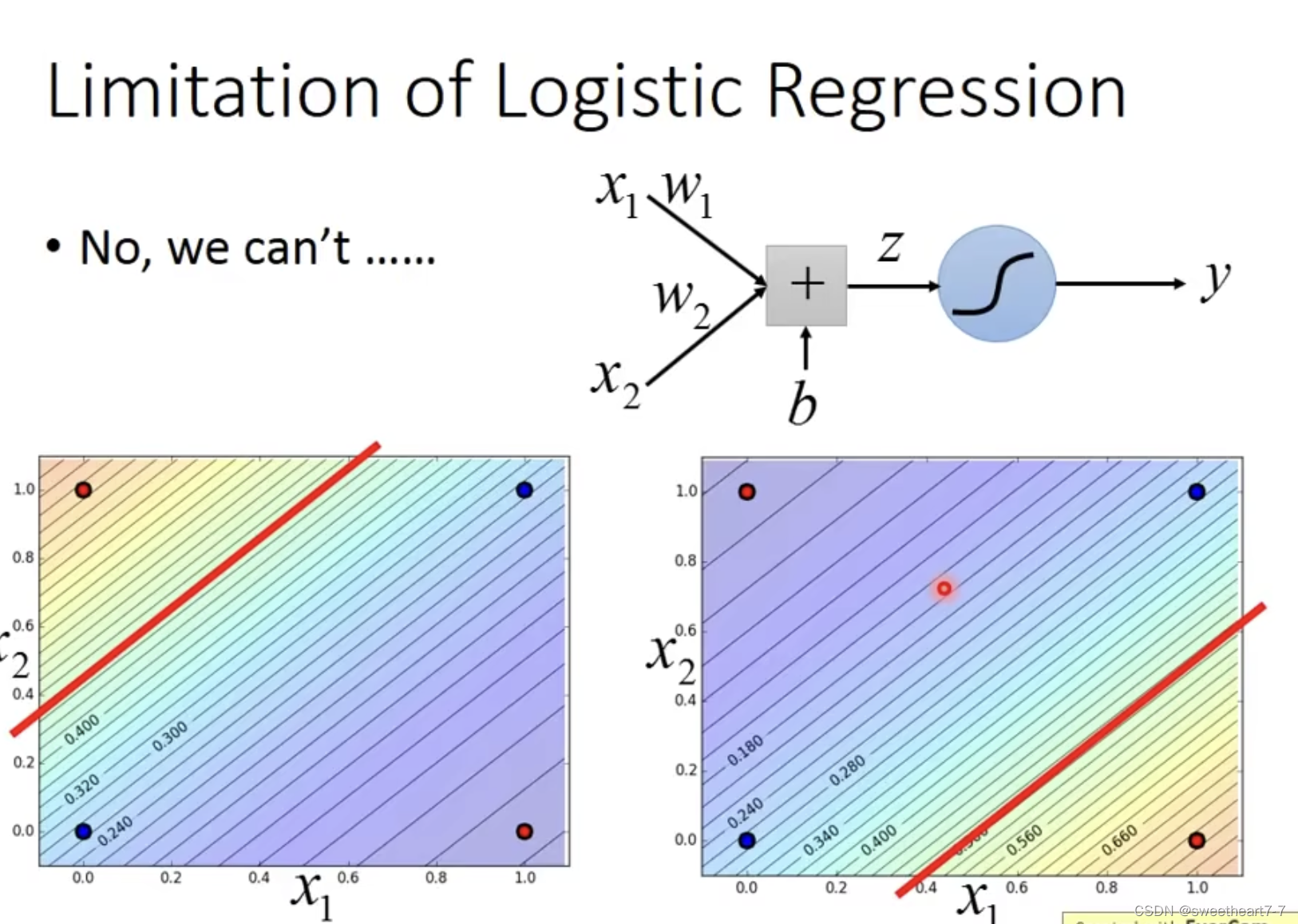
So we can consider pairs of features (feature) 进行转换,Then use logistic regression to solve it

可以将 logistic regression models 多个 cascading 起来,Let the machine find it by itself feature transformation

What the machine finds out is as follows：

可以把这些 Logistic Regression 叠在一起,某一个 Logistic Regression 可以是其他 Logistic Regression 的 output.

可以给这个 Model 一个新名字：Neural Network (Deep learning)