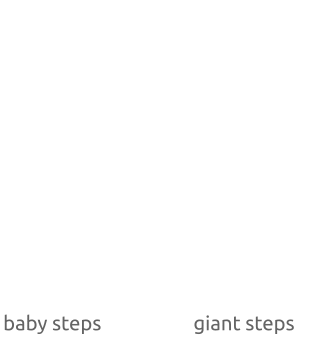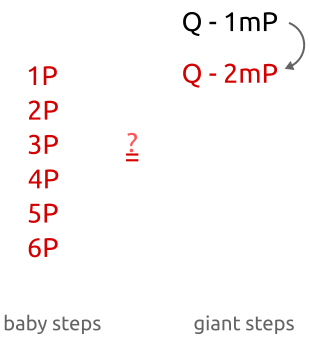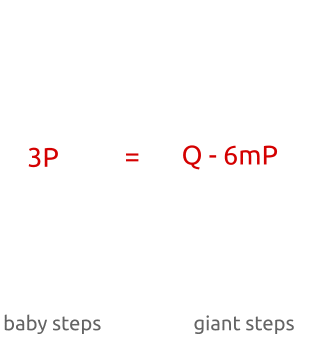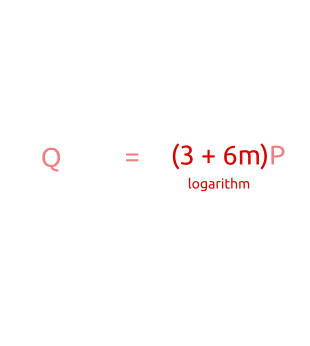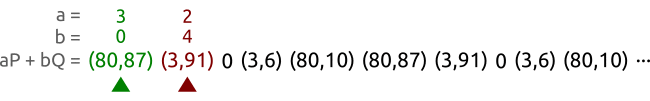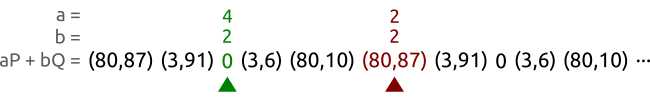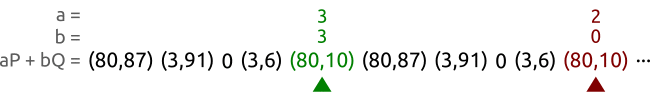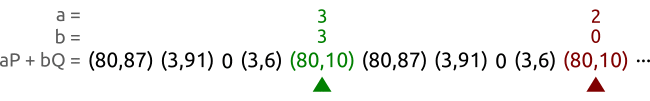当前位置:网站首页>Introduction to Elliptic Curves (4): Elliptic Curve Security, Compared with RSA
Introduction to Elliptic Curves (4): Elliptic Curve Security, Compared with RSA
2022-08-06 03:22:00 【AdijeShen】
内容来自ANDREA CORBELLINI的椭圆曲线密码学的介绍:Elliptic Curve Cryptography: a gentle introduction
The fourth article is elliptic curve is introduced in this paper:The security of elliptic curve part.
在上一篇博客中,We have introduced two kinds of elliptic curve cryptography algorithms above:ECDH和ECDSA.Notice the two algorithms are based on the safety of the椭圆曲线中的离散对数问题.但是,Haven't the rigorous mathematical proof shows that the discrete logarithm problem is really difficult,Just community formed a consensus,Is there any evidence that can make us believe that this consensus?
So in the first part of this blog,We will be to sort out椭圆曲线中的离散对数问题How difficult is it to solve.
在第二部分,We answer the following question:为什么RSA类型(Arithmetic module type)The password system has so many useful algorithm,Also need to be put forward based on elliptic curve cryptography algorithm.
文章目录
To solve the discrete logarithm problem
We need to introduce two kinds of efficient computing method of elliptic curve discrete logarithm:1.baby-step,giant-step方法,小步大步法.2.Pollard’s rho方法.
Before beginning to introduce these two methods,Recall the discrete logarithm problem is what:给定两个点 P P P和 Q Q Q,计算出一个数字 x x x使得 Q = x P Q=xP Q=xP. P P P和 Q Q QTwo belong to the same subgroup on the elliptic curve,The subgroup generated RMB as G G G,阶为 n n n.
小步大步法(Baby-step, giant-step)
在开始介绍算法之前,先想一想,We can be any integer writing x = a m + b x=am+b x=am+b.比如 10 = 2 ⋅ 3 + 4 10=2\cdot 3+4 10=2⋅3+4.
因此,Can also be in the form of the discrete logarithm problem is converted into a:
Q = x P Q = ( a m + b ) P Q = a m P + b P Q − a m P = b P \begin{aligned} Q&=xP\\ Q&=(am+b)P\\ Q&=amP+bP\\ Q-amP&=bP \end{aligned} QQQQ−amP=xP=(am+b)P=amP+bP=bP
Small big footwork is more like a compromise solution,Compared with violent search,We only need to compute a few b P bP bP的值,以及几个 Q − a m P Q-amP Q−amP的值.算法的步骤如下:
- 计算 m = ⌈ n ⌉ m=\lceil \sqrt{n} \rceil m=⌈n⌉
- 对于 b ∈ { 0 , . . . , m } b \in \{0,...,m\} b∈{ 0,...,m},计算 b P bP bPCoexist in a hash table.
- 对于 a ∈ { 0 , . . . , m } a \in \{0,...,m\} a∈{ 0,...,m}:
- 计算 a m P amP amP;
- 计算 Q − a m P Q-amP Q−amP;
- 查看哈希表中是否存在 Q − a m P = b P Q-amP=bP Q−amP=bP;
- 如果存在的话,那就返回 x = a m + b x=am+b x=am+b.
可以观察到,A starting point b P bP bP之间的差距为 1 1 1,As small step,然后在第二部分中,The gap between the two points as m m m,其中 m m m是一个很大的数字,So remember as a big step.
小步大步法,First step calculate several points coexist in the hash table.Then use the big moves to find matching points.
Explain why the algorithm below is right,Only with small step how to ensure that all elements are traversing the.我们知道 Q = a m P + b P Q=amP+bP Q=amP+bP,那考虑:
- 当 a = 0 a=0 a=0的时候,We will verify whether Q = b P Q=bP Q=bP,因为 b b b是在 0 0 0到 m m m中的一个数,So we are in the confirmation Q Q Q是否为 0 P 0P 0P到 m P mP mP.
- 当 a = 1 a=1 a=1的时候,We verify Q = m P + b P Q=mP+bP Q=mP+bP,We are confirmed Q Q Q是否为 m P mP mP到 2 m P 2mP 2mP.
- 当 a = 2 a=2 a=2的时候,We are confirmed Q Q Q是否为 2 m P 2mP 2mP到 3 m P 3mP 3mP.
- …
- 当 a = m − 1 a=m-1 a=m−1的时候,We are confirmed Q Q Q是否为 ( m − 1 ) m P (m-1)mP (m−1)mP到 m 2 P = n P m^2P=nP m2P=nP.
因此,We are confirmed Q Q Q是否为 0 P 0P 0P到 n P nP nP中的某个点,And we only perform 2 m 2m 2mAddition or multiplication operation.
If the query the complexity of the hash table to remember O ( 1 ) O(1) O(1),那么这个算法的时间复杂度为 O ( n ) O(\sqrt{n}) O(n),空间复杂度为 O ( 2 k ) O(2^{k}) O(2k), k k kFor point bit length.Although still is the exponential time,But it's much better than violence search has.
Pollard’s ρ \rho ρ方法
Pollard的rhoMethods and steps as it is a big step O ( n ) O(\sqrt{n}) O(n)复杂度的算法,But the space complexity just O ( 1 ) O(1) O(1).
What is recall the discrete logarithm problem again:给定两个点 P P P和 Q Q Q,计算出一个数字 x x x使得 Q = x P Q=xP Q=xP.在Pollard’s ρ \rho ρ方法中,We solve the problem is slightly different:给定两个点 P P P和 Q Q Q,找到四个数 a , b , A , B a,b,A,B a,b,A,B满足 a P + b Q = A P + B Q aP+bQ=AP+BQ aP+bQ=AP+BQ.
If you can find such a formula,Then you can use this formula to solve the discrete logarithm problem:
a P + b Q = A P + B Q a P + b x P = A P + B x P ( a + b x ) P = ( A + B x ) P ( a − A ) P = ( B − b ) x P \begin{aligned} a P+b Q &=A P+B Q \\ a P+b x P &=A P+B x P \\ (a+b x) P &=(A+B x) P \\ (a-A) P &=(B-b) x P \end{aligned} aP+bQaP+bxP(a+bx)P(a−A)P=AP+BQ=AP+BxP=(A+Bx)P=(B−b)xP
You can now by both sides in addition to P P P的方式来消除 P P P,Don't forget all the coefficients are in m o d n \bmod n modn范围内的,因此:
a − A ≡ ( B − b ) x m o d n x = ( a − A ) ( B − b ) − 1 m o d n \begin{aligned} a-A & \equiv(B-b) x \quad\bmod n \\ x &=(a-A)(B-b)^{-1} \bmod n \end{aligned} a−Ax≡(B−b)xmodn=(a−A)(B−b)−1modn
Pollard rhoThe purpose of the method is very simple,We randomly generated some point X 1 , X 2 , . . . X_1,X_2,... X1,X2,...,其中 X i = a i P + b i Q X_i = a_iP + b_iQ Xi=aiP+biQ.Can be used to generate pseudo random function:
( a i + 1 , b i + 1 ) = f ( X i ) (a_{i+1},b_{i+1})=f(X_i) (ai+1,bi+1)=f(Xi)
这个函数的意思是,将 X i X_i Xi作为输入,得到 X i + 1 X_{i+1} Xi+1的系数 a i + 1 , b i + 1 a_{i+1},b_{i+1} ai+1,bi+1,Then you can again X i + 1 X_{i+1} Xi+1作为输入,继续运算,This process can be operation continues.
f f fThe internal logic of actually it doesn't matter,重要的是 f f fIs obtained from the current point to the next point,而所有 f f f得到的 a i , b i a_i,b_i ai,bi我们都是知道的.
As long as the operation continues,We always get a loop,也就是找到了 X j = X i X_j=X_i Xj=Xi.

As for why will appear this cycle,理由很简单:Of the elliptic curve group, there is a limit to the amount of,So it will be a loop.Once we have met a cycle,Then you can to solve the discrete logarithm problem.
Now the new problems to the:How to quickly find such a cycle?
龟兔赛跑
A faster method of looking for circulation is a method of the tortoise and the hare.The figure below shows the principle of method of the tortoise and the hare,其实也是Pollard’s rho方法.
Such as curve y 2 ≡ x 3 + 2 x + 3 ( m o d 97 ) y^2 \equiv x^3 +2x +3 \pmod{97} y2≡x3+2x+3(mod97),上面的点为 P = ( 3 , 6 ) P=(3,6) P=(3,6),以及 Q = ( 80 , 87 ) Q=(80,87) Q=(80,87).These points belong to an order for5的子群.We use two different parameters ( a , b ) ( A , B ) (a,b)(A,B) (a,b)(A,B)To traverse these a P + b Q aP+bQ aP+bQ的对,Until they are equal to a point.在上面的例子中,我们找到了 ( 3 , 3 ) (3,3) (3,3)和 ( 2 , 0 ) (2,0) (2,0)是一样的,于是就可以计算出 x = ( 3 − 2 ) ( 0 − 3 ) − 1 m o d 5 = 3 x=(3-2)(0-3)^{-1}\bmod 5 =3 x=(3−2)(0−3)−1mod5=3.Then it is concluded that the discrete logarithm problem solution: Q = 3 P Q=3P Q=3P.
We select two animals:乌龟和兔子,Let them run from left to right.乌龟(绿点)Than the red dot(兔子)The speed of the slower.A tortoise walk a,A rabbit go two.
过了一段时间之后,Tortoise and the rabbit found a the same point,But their parameters something different.Or use the parameter to represent,Is the tortoise found a pair of parameters ( a , b ) (a,b) (a,b),The rabbit find hit a pair of parameters ( A , B ) (A,B) (A,B),使得 a P + b Q = A P + B Q aP+bQ=AP+BQ aP+bQ=AP+BQ.
Is easy to see such a scheme only needs constant memory( O ( 1 ) O(1) O(1)的空间复杂度).Time complexity is not very good calculation,But can be by a probability proof time complexity is O ( n ) O(\sqrt{n}) O(n)级别的.这个证明是基于生日悖论的:Birthday paradox to consider is the probability of two personal birthday is the same,And we consider two pairs ( a , b ) (a,b) (a,b)To get the same probability.
The efficiency of algorithm attack contrast
The exhaustive algorithm,pollard’s rho算法,Small step footwork together to compare,代码放在这里"Several elliptic curve attack algorithms comparedpython代码".
运行结果如下:
Curve order: 10331
Using bruteforce
Computing all logarithms: 100.00% done
Took 2m 31s (5193 steps on average)
Using babygiantstep
Computing all logarithms: 100.00% done
Took 0m 6s (152 steps on average)
Using pollardsrho
Computing all logarithms: 100.00% done
Took 0m 21s (138 steps on average)
It's not hard to guess to exhaustion is the slowest.Small big moves the fastest,Pollard’s rhoMethods almost three times slower than big step footwork around.(Despite his steps and use the least amount of memory).
Also can have a look at these three algorithms from the average number,Exhaustion, on average, with the5193步,General order elliptic curve is basically.Small big gaits andPollard’s rhoMethods are close to10331The square root of the number of.
最后的总结
Although we discussed several methods,They could not efficiently break the elliptic curve discrete logarithm problem.But do not represent these algorithms completely is not possible,Maybe can continue to do optimization,Such as hardware breakthrough.
Although there is no method to solve the discrete logarithm problem of,But don't represent the future there will be no.
Shor的算法
Although today's approach is not feasible,But the future quantum computers,There is a quantum algorithm can decode the discrete logarithm problem,他就是Shor算法.它的时间复杂度为 O ( log n ) 3 O(\log n)^3 O(logn)3,空间复杂度为 O ( log n ) O(\log n) O(logn).
Although quantum computing is not enough to run nowShor算法,But after toward quantum cryptography migration has been a necessary things.Today we use encryption algorithm is safe,Do not represent tomorrow he also safe.
ECC和RSA对比
Now the quantum computer first put aside,That's after the problem.现在的问题是,Has been in thereRSA的情况下,为什么还需要ECC的算法?
NISTGave a direct answer,They are given the same level of security to the two algorithm's key size:
| RSA key size (bits) | ECC key size (bits) |
|---|---|
| 1024 | 160 |
| 2048 | 224 |
| 3072 | 256 |
| 7680 | 384 |
| 15360 | 521 |
注意到RSAThe length of keys andECCThere is no linear relationship between the length of keys.也就是说,RSAThe key of up to twice the case,ECCNo double.而且ECCNot only store the keys overhead is small,And key generation and signature operation thanRSA要快很多.
但为什么会这样呢?因为解决ECCThe discrete logarithm problem is more difficult than solving the limited domain of discrete logarithm.The discrete logarithm problem of integer above generally is through普通数域筛选法,Can be resolved faster integer,To solve the discrete logarithm problem.
NSAThe danger behind
We discussed so far are the problems of algorithm and the count.But there is one more important and complicated factors,就是人.
In a blog, we mentioned some of the elliptic curve is safe,In order to prevent the curve of the unknown source,We adopt the method of the random number seed to generate global parameters.如果我们看一下NISTReleased by the elliptic curve,We can verify they are generated by random number.
If we searchNothing up my sleeve number,可以看到:
- MD5Random number by integer arithmeticsin函数得到的
- Blowfish的随机数是 π \pi π的前几位
- RC5Random number is from natural logarithm e e eAnd the golden
These Numbers we can believe that they are random.Because we can demonstrate the number.
而NISTReleased by the random number seed is how come?,我们不知道.So all the random number seed is no credibility.
NISTIs it possible to by exhaustive random number seed found a not secure elliptic curve and released them? 也不是没可能.目前来说NIST已经有Reported unsafe random number generatorThe criminal record.So they have released a crime may not secure elliptic curve(doge).
Considering the parameters of the elliptic curve problem,Actually this isRSA胜出的,因为RSADo not need to specify a prime number,Only need long enough can.And elliptic curve carefully chosen to avoid some unsafe parameters.
但NISTThe release of elliptic curve now use more?答案是是的,在TLSLayer with theNIST的曲线,If the search will find nowECDHE和ECDSA,Their certificate is based onprime256v1(也就是secp256p1).
边栏推荐
- LeetCode:623. 在二叉树中增加一行【DFS or BFS】
- leetcode 17. Letter Combinations of Phone Numbers
- What are the big events on Tmall in August 2022?
- django报错 ModuleNotFoundError: No module named 'mysqlclient'
- Detailed description of hand-eye calibration (introduction of coordinate system, two-dimensional, three-dimensional hand-eye calibration method @ nine-point method, AX=XB)
- Lvm根分区扩容
- KGAT recommendation system
- Two implementations of vtk patch hole
- 智能合约安全-整数溢出(SW101-IntegerOverflowAndUnderflow)
- 网络安全辅助工具:免费MD5解密网站
猜你喜欢

实现Redis主从复制
Log Management Lombok Profile

WeChat applet multi-select - four choose two

Entering the pit of machine learning: 2. Supervised learning

Two implementations of vtk patch hole

LeetCode:623. 在二叉树中增加一行【DFS or BFS】

leetcode 17. Letter Combinations of Phone Numbers
KU115 PCIE总线数据预处理板卡(多LVDS接口)

6.软件测试-----自动化测试之unittest框架

实心轮胎的优缺点
随机推荐
django报错 ModuleNotFoundError: No module named 'mysqlclient'
2022年天猫8月份有什么大的活动?
NetCore - custom exception handling
C 学生管理系统 删除指定学生节点(特殊情况)
入坑机器学习:三,非监督学习
xctf attack and defense world web master advanced area command_execution
【Untitled】
The Google account was suspended for three months and reactivated, and the Google account was suspended for three months and reactivated. Is the conversion goal valid?
What is an inner class?
C 学生管理系统 打印/修改指定位置信息
又双叒叕有捷报传来
Use BeanUtils with caution, the performance really stretches!
leetcode:1374. 生成每种字符都是奇数个的字符串
cocos小游戏实战-完结
物联网协议概述
pytest之assert断言的使用
Web3.exceptions.ExtraDataLengthError
新搭建的国家广告系列,是否要排除掉旧的广告系列?
ALV细节再梳理2022.8.5
Detailed description of hand-eye calibration (introduction of coordinate system, two-dimensional, three-dimensional hand-eye calibration method @ nine-point method, AX=XB)