一、伪逆概述

        并非所有矩阵都有逆矩阵。逆用于求解方程组，在某些情况下，方程组没有解，因此逆不存在。然而，找到一个最小化误差的近似值是有意义的。例如，使用伪逆找到一组数据点的最佳拟合线。

        Moore-Penrose 伪逆是SVD的直接应用。

        正如我们在之前篇章中看到的，矩阵A的逆矩阵可用于求解方程Ax=b：

        

         但是在方程组有0个或多个解的情况下，无法找到逆，也无法求解方程，这时候需要伪逆上场了。

        伪逆记作​​​​​​​，并，并最小化

         以下公式可用于求伪逆：

        

        （1）U、D 和 V 分别是 A 的左奇异向量、奇异值和右奇异向量。

        （2）是A的伪逆，是D的伪逆。

        （3）我们知道D是对角矩阵，因此D+可以通过取D的非零值的倒数来计算。

 二、例1：伪逆计算

         让我们看看如何计算它。 我们将创建一个非方阵 A，计算其奇异值分解及其伪逆。

        

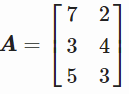
A = np.array([[7, 2], [3, 4], [5, 3]])
U, D, V = np.linalg.svd(A)

D_plus = np.zeros((A.shape[0], A.shape[1])).T
D_plus[:D.shape[0], :D.shape[0]] = np.linalg.inv(np.diag(D))

A_plus = V.T.dot(D_plus).dot(U.T)

        求得A_plus

array([[ 0.16666667, -0.10606061,  0.03030303],
       [-0.16666667,  0.28787879,  0.06060606]])

          我们现在可以使用 Numpy 的 pinv() 函数检查伪逆是否正确：

np.linalg.pinv(A)

        求得

array([[ 0.16666667, -0.10606061,  0.03030303],
       [-0.16666667,  0.28787879,  0.06060606]])

        数据一致，我们现在可以检查它是否真的是 A 的近似倒数。

        我们已知并且

A_plus.dot(A)

         求得下面的矩阵，可以看出近似单位矩阵，对吧。

array([[  1.00000000e+00,   2.63677968e-16],
       [  5.55111512e-17,   1.00000000e+00]])

        就是说，也就是

        计算伪逆的另一种方法是使用以下公式：

        

A_plus_1 = np.linalg.inv(A.T.dot(A)).dot(A.T)

        对于不同矩阵结果不如SVD方法精准。Numpy的函数pinv()就是使用SVD。

三、例2：使用伪逆求解超定线性方程组

        对于这个例子，我们将考虑这组三个具有两个未知数的方程：

        

        让我们可视化

x1 = np.linspace(-5, 5, 1000)
x2_1 = -2*x1 + 2
x2_2 = 4*x1 + 8
x2_3 = -1*x1 + 2

plt.plot(x1, x2_1)
plt.plot(x1, x2_2)
plt.plot(x1, x2_3)
plt.xlim(-2., 1)
plt.ylim(1, 5)
plt.show()

         可视化效果如下，三条线没有交与一点，就是没有解。伪逆从最小二乘误差的角度求解系统：它找到最小化误差的解。

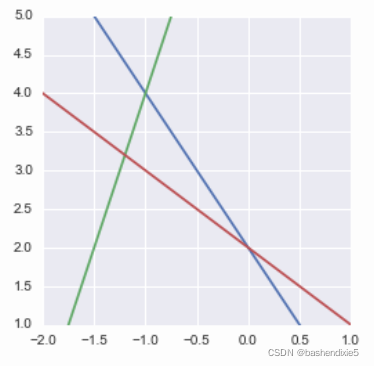
         我们用矩阵形式表示

        

        即

        我们现在将计算 A 的伪逆：

A = np.array([[-2, -1], [4, -1], [-1, -1]])
A_plus = np.linalg.pinv(A)
A_plus

         求得

array([[-0.11290323,  0.17741935, -0.06451613],
       [-0.37096774, -0.27419355, -0.35483871]])

         取四位小数即，

         我们可以用它来找到 x：、

b = np.array([[-2], [-8], [-2]])
res = A_plus.dot(b)
res

         求得

array([[-1.06451613],
       [ 3.64516129]])

         即x坐标

        让我们绘制到图上看一下

plt.plot(x1, x2_1)
plt.plot(x1, x2_2)
plt.plot(x1, x2_3)
plt.xlim(-2., 1)
plt.ylim(1, 5)

plt.scatter(res[0], res[1])

plt.show()

         可视化效果如下

         也许您会期望该点位于三角形的重心处。但情况并非如此，因为方程的缩放方式不同。

四、例3：直线拟合

        此方法还可用于将线拟合到一组点。设有以下数据点：

         我们现有这组 x 和 y，我们要寻找最小化误差的线 y=mx+b。 可以将误差评估为拟合和实际数据点之间的差异之和。

        我们可以用矩阵方程表示数据点：

        

         请注意，这里的矩阵 A 表示系数的值。 1 列对应于截距（没有它，拟合将有跨越原点的约束）。 它给出了以下方程组：

        

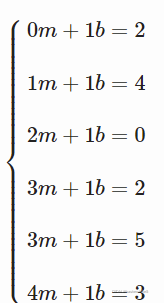
        我们有一组方程 mx+b=y。 这些用于返回截距参数。 例如，在对应于第一个点的第一个方程中，我们有很好的 x=0 和 y=2。 这可能会令人迷惑，因为这里的向量 x 对应于系数。 这是因为我们正在寻找直线的系数而不是 x 和 y 未知数。

         所以我们将构造这些矩阵并尝试使用伪逆来找到最小化误差（线与实际数据点之间的差异）的线的方程。

        让我们创建 A 和 b 的矩阵并计算A的伪逆：

A = np.array([[0, 1], [1, 1], [2, 1], [3, 1], [3, 1], [4, 1]])
b = np.array([[2], [4], [0], [2], [5], [3]])
A_plus = np.linalg.pinv(A)

        求得伪逆如下

array([[ -2.00000000e-01,  -1.07692308e-01,  -1.53846154e-02,
          7.69230769e-02,   7.69230769e-02,   1.69230769e-01],
       [  6.00000000e-01,   4.00000000e-01,   2.00000000e-01,
          4.16333634e-17,   4.16333634e-17,  -2.00000000e-01]])

        带入公式x=A+b

coefs = A_plus.dot(b)

        求得拟合的参数。 斜率为 m=0.21538462，截距为 b=2.2。

array([[ 0.21538462],
       [ 2.2       ]])

        我们将绘制数据点和回归线：

x = np.linspace(-1, 5, 1000)
y = coefs[0]*x + coefs[1]

plt.plot(A[:, 0], b, '*')
plt.plot(x, y)
plt.xlim(-1., 6)
plt.ylim(-0.5, 5.5)

plt.show()

        使用numpy库进行核验，使用polyfit函数对A和b进行拟合，得到如下结果，说明计算无误。

np.polyfit(A[:, 0], b, 1)

array([[ 0.21538462],
       [ 2.2       ]])

         还有很多计算库或者在线拟合网页可以验证上面的计算，可以自行尝试。

五、例4：直线拟合

        要查看具有更多数据点的过程，我们可以生成数据。

        我们将生成一个包含 100 个具有随机 x 值和伪随机 y 值的点的列向量（参见下面的 reshape()）。 Numpy.random 包中的函数 seed() 用于冻结随机化并能够重现结果：

np.random.seed(123)
x = 5*np.random.rand(100)
y = 2*x + 1 + np.random.randn(100)

x = x.reshape(100, 1)
y = y.reshape(100, 1)

        我们将通过添加一列 1 从 x 创建矩阵 A，就像我们在示例 3 中一样。

A = np.hstack((x, np.ones(np.shape(x))))
A[:10]

        得到

array([[ 3.48234593,  1.        ],
       [ 1.43069667,  1.        ],
       [ 1.13425727,  1.        ],
       [ 2.75657385,  1.        ],
       [ 3.59734485,  1.        ],
       [ 2.1155323 ,  1.        ],
       [ 4.90382099,  1.        ],
       [ 3.42414869,  1.        ],
       [ 2.40465951,  1.        ],
       [ 1.96058759,  1.        ]])

        我们现在可以找到 A 的伪逆并计算回归线的系数：

A_plus = np.linalg.pinv(A)
coefs = A_plus.dot(y)
coefs

        求得

array([[ 1.9461907 ],
       [ 1.16994745]])

        我们将点和直线可视化

x_line = np.linspace(0, 5, 1000)
y_line = coefs[0]*x_line + coefs[1]

plt.plot(x, y, '*')
plt.plot(x_line, y_line)
plt.show()

六、其它参考

        您可以看到伪逆对这类问题非常有用！另外关于多项式拟合或拟合平面可以参考以下文章。

Opencv学习笔记 - 多项式求解和拟合_bashendixie5的博客-CSDN博客_opencv 多项式拟合曲线的函数类型有:双曲线型、对数型、指数型、多项式型等。对于最常见的曲线, 其特征接近于多项式型, 所以这里的曲线拟合问题就变成了多项式回归求解.一般情况下,对实际的点数据进行求解是无解的, 所以我们需要引入最小二乘法来求解。https://blog.csdn.net/bashendixie5/article/details/115176277Opencv学习笔记 - 使用最小二乘法拟合平面_bashendixie5的博客-CSDN博客_opencv 平面拟合https://blog.csdn.net/u012719076/article/details/113124887https://blog.csdn.net/liumangmao1314/article/details/54179526本文主要验证了博客上的最小二乘法拟合平面的。与 用matlab拟合出来的平面计算的点到直线的距离是一样的，而且系数也是一样的。说明了本方法的可行性。matlab中公式为z = c + ax +byoepncv中公式为Ax+By+Cz=D 将openc..https://blog.csdn.net/bashendixie5/article/details/115413982