Start with the simplest example,We want to sum an array,One way to take it for granted is to directly traverse and sum,Let's see if we can consider recursion.

递归算法是一种直接或者间接调用自身函数或者方法的算法.说简单了就是程序自身的调用.递归算法就是将原问题不断分解为规模缩小的子问题,然后递归调用方法来表示问题的解.（用同一个方法去解决规模不同的问题）

• 递去：将递归问题分解为若干个规模较小,与原问题形式相同的子问题,这些子问题可以用相同的解题思路来解决
• 归来：当你将问题不断缩小规模递去的时候,必须有一个明确的结束递去的临界点（递归出口）,一旦达到这个临界点即就从该点原路返回到原点,最终问题得到解决.
  四、The design elements of the recursive algorithm

Recursive thinking is a bottom-up way of thinking,Using recursive algorithms can often simplify our code,And also help us solve very complex problems.The difficulty of recursive algorithm lies in its logic,In general, the design of recursive algorithms needs to consider the following points:

1. Explicitly recursive termination condition
2. 提取重复的逻辑,Reduce the size of the problem and keep passing
3. 给出递归终止时的处理办法

什么时候使用递归

Determining whether a problem can use recursion is the beginning of mastering recursion.Let's look at some classic recursion problems

1. 顺序打印链表

看到这个问题,The most simple idea is the loop,To be honest, I think it is a problem with my brain when I consider using recursion to solve it.,Helpless, in order to slowly understand recursion, I can only forcibly lean up..
When I think about it, it's very direct,print the current number,Then the recursive call itself keeps shrinking the problem size

# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None

class Solution:
    def printList(self, head: ListNode) -> List[int]:
        if head is None:
            return
        print(head.val)
        self.printList(head.next)

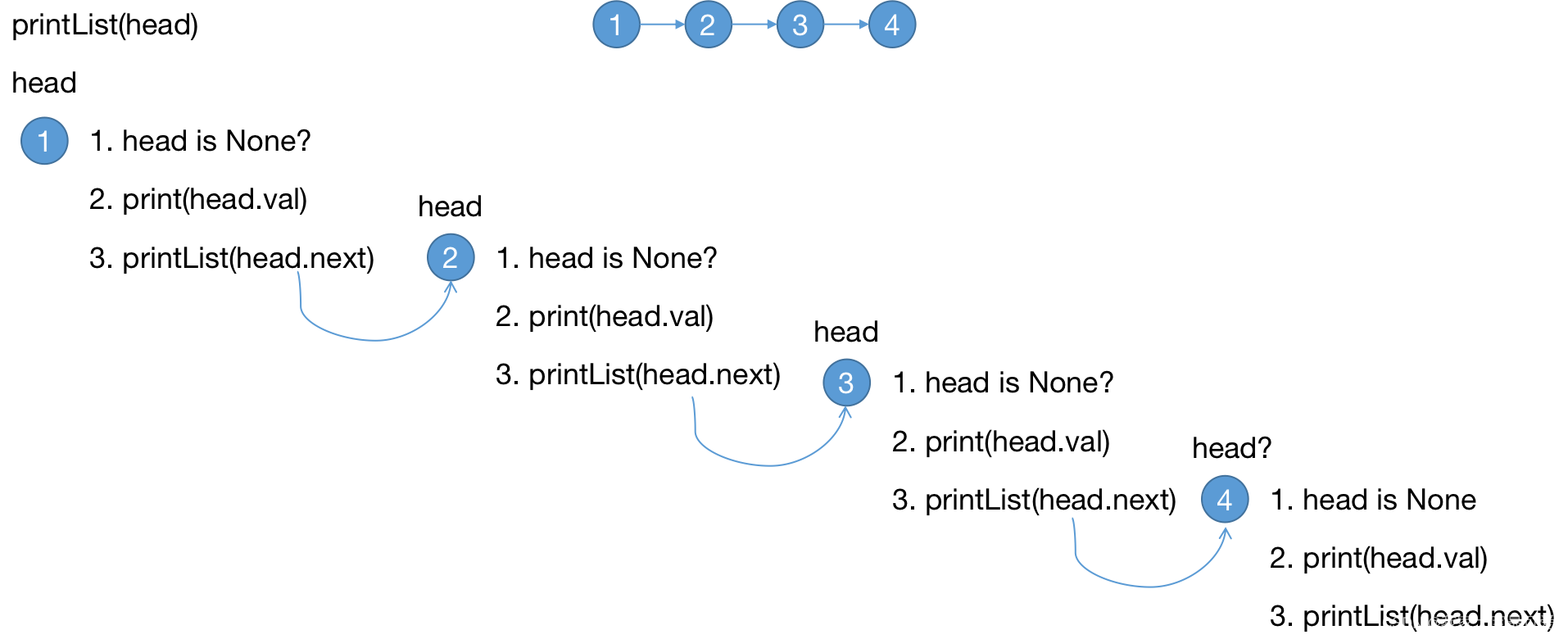
1. Clarified the stop condition for recursion,head is NoneIt's time to reach the end of the linked list,No further printing is required so it can be stopped
2. 提取重复的逻辑,The repetition logic here is very simple,就是print(head.val)
3. 缩小问题规模,我们不断调用head.next,使得headmove to the back of the list,downsizing the problem
4. We don't need to do anything else when the recursion terminates,因此直接返回即可

老实讲,The recursion here is actuallyfor循环,We keep traversing backwards.

2. 链表求和

Linked list summation and printing are the same,We use recursion to traverse each element and sum it up.But here we consider recursive subproblems.

It can also be easily understood from the above figure,We can reduce the size of the problem,想要求解sum([1,2,3,4,5,6,7]),我们只要先求出sum([2,3,4,5,6,7])的结果,然后再跟head.val相加即可.同样的套娃方式,我们想要求解sum([2,3,4,5,6,7]),只需要求解sum([3,4,5,6,7])即可.

# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None

class Solution:
    def listSum(self, head: ListNode) -> List[int]:
        if head is None:
            return 0
        s = self.listSum(head.next) + head.val # 子问题
        return s # 其他逻辑

1. Clear the termination conditions,当head is Noneyou don't need to add any more,At this point we can return0
2. 提取重复逻辑,The repetition logic here is also simple,It is to accumulate the current value and the value of the sub-problemself.listSum(head.next) + head.val

3. 数组求和

The recursion of array summation is my own blind thinking,Mainly want to use the idea of ​​merge,We still divide the original problem into sub-problems,to reduce the size of the problem.But here we need to call the subproblem twice,We divide the array into two parts,Then solve the sum of the left array separately,And on the right side of the array,Then adding them together is the total sum

This question is also a good illustration of a feature of recursion,that is to reduce the size of the problem,The subproblem is equivalent to the original problem,After we solve the subproblem,Some more logical operations are required.Suddenly a question comes to mind,Is the subproblem equivalent to the original problem?？

1. Logically it must be the same,只是问题规模缩小了.
2. Those logical operations are the problem-solving

arr = [-1,2,3,4,5,6]

def mergeAdd(arr, l,r):
    if l >= r:
        return arr[l]
    
    m = (l + r) // 2

    lsum = mergeAdd(arr, l, m)
    rsum = mergeAdd(arr, m+1, r)

    return lsum + rsum

res = mergeAdd(arr,0,len(arr)-1)
print(res)

1. 终止条件,When the left cursor is greater than or equal to the right cursor,说明只有一个元素了,At this point, you can directly return the value
2. Subproblems and repetition logic,The original solution was0到len(arr)-1所有元素的和,Now solve the subproblem0到m和子问题m+1到len(arr)-1和,subproblem called twice,The sums solved are then added together to obtain the total sum