当前位置:网站首页>Leetcode39 combined sum
Leetcode39 combined sum
2022-04-23 02:01:00 【Xicheng Fengyu building】
LeetCode39- Combinatorial summation
One 、 Title Description

Two 、 Topic analysis
2.1 Backtracking tree
Combinatorial problem is a typical problem that needs to be solved by backtracking algorithm , When dealing with backtracking algorithms , Think about the structure of the backtracking tree , And try to draw the backtracking tree of the problem , When drawing the backtracking tree , Pay attention to a special requirement in the title :
There is no limit to the same number, The following is an illustration of the backtracking tree ( With[2,3,6,7]For example ):

2.2 Recursive termination condition
According to the title, it is easy to think of at least two termination conditions :
(1) The sum on the current traversal path is equal to target When , Then collect the results , And no recursion at the next level
(2) The sum on the current traversal path is greater than target When , Then this path can be pruned directly , No recursion at the next level
3、 ... and 、 Basic code implementation
class Solution {
public List<List<Integer>> combinationSum(int[] candidates, int target) {
List<List<Integer>> res = new ArrayList<>();
solve(candidates, target, res, new ArrayList<>(), 0, 0);
return res;
}
// curRes Store the nodes in the current path
// curSum Store the sum of the current path node
// res Used to collect all sequences that meet the conditions
public void solve(int[] candidates, int target, List<List<Integer>> res,List<Integer> curRes, int startIndex, int curSum) {
if (curSum == target) {
res.add(new ArrayList<>(curRes));
return;
}
if (curSum > target) {
return;
}
for (int i = startIndex; i < candidates.length; i += 1) {
curSum += candidates[i];
curRes.add(candidates[i]);
solve(candidates, target, res, curRes, i, curSum);
curSum -= candidates[i];
curRes.remove(curRes.size() - 1);
}
}
}
Four 、 Further optimization
The two recursive termination conditions given above can only be regarded as the basic bound conditions of backtracking algorithm , Used to terminate recursion , But we don't give the pruning condition of backtracking algorithm ,curSum > target You can only cut the branches under the same path , You can't cut off branches on the same layer , In fact, in the process of backtracking ,
When we need to extend nodes of the same layer ( namely for In the cycle ), If the nodes of the same layer are extended in ascending order ( Just sort the original array in ascending order ), Then we can also prune, The condition for pruning is stillcurSum > target, The optimized code is as follows :
class Solution {
public List<List<Integer>> combinationSum(int[] candidates, int target) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(candidates);
solve(candidates, target, res, new ArrayList<>(), 0, 0);
return res;
}
/** * Solve the combinatorial summation problem by backtracking algorithm * * @param candidates * @param target * @param res Store all results that meet the conditions * @param curRes Store the results that meet the conditions in the current search path * @param startIndex The index at the beginning of each layer */
public void solve(int[] candidates,
int target, List<List<Integer>> res,
List<Integer> curRes, int startIndex, int curSum) {
if (curSum == target) {
res.add(new ArrayList<>(curRes));
return;
}
if (curSum > target) {
// Only the branches under the same path can be cut here
return;
}
for (int i = startIndex; i < candidates.length; i += 1) {
curSum += candidates[i];
if (curSum > target) {
// Cut off the branches of the same layer , namely for The loop is no longer extended
break;
}
curRes.add(candidates[i]);
solve(candidates, target, res, curRes, i, curSum);
curSum -= candidates[i];
curRes.remove(curRes.size() - 1);
}
}
}
5、 ... and 、 Submit results

版权声明
本文为[Xicheng Fengyu building]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204220844276829.html
边栏推荐
- Encrypted compressed backup bat script
- Esp32 message queue using FreeRTOS
- What categories do you need to know before using proxy IP?
- 使用代理IP是需要注意什么?
- 如何选择一台好的拨号服务器?
- 如何“优雅”的测量系统性能
- Do447 manage user and team access
- What code needs unit testing?
- 2018 China Collegiate Programming Contest - Guilin Site J. stone game
- EBS:PO_EMPLOYEE_HIERARCHIES_ALL
猜你喜欢

PHP & laravel & master several ways of generating token by API and some precautions (PIT)

Error in face detection and signature of Tencent cloud interface

有哪些常见的代理ip问题?

Find the largest number of two-dimensional arrays
![[hands on learning] network depth v2.1 Sequence model](/img/51/0de4c7972a99151007a8f27f351c83.png)
[hands on learning] network depth v2.1 Sequence model

什么是api接口?

一些使用代理IP的小技巧。

Shardingsphere introduction and sub table usage
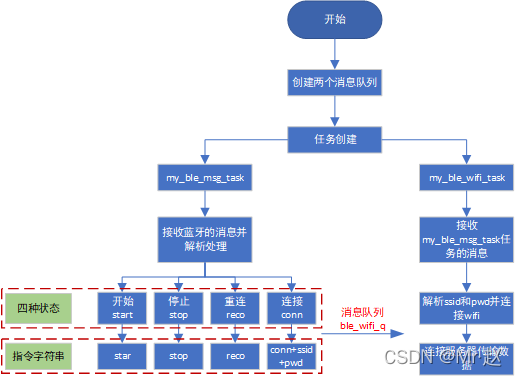
W801 / w800 WiFi socket development (II) - UDP Bluetooth control WiFi connection

使用代理IP是需要注意什么?
随机推荐
如何对代理IP进行分类?
关于局域网浅谈
J-Link RTT使用
What are the test steps of dynamic proxy IP?
English abbreviation of role personal attribute
C语言实现Base64编码/解码
2022 low voltage electrician examination questions and answers
如何“优雅”的测量系统性能
PHP & laravel & master several ways of generating token by API and some precautions (PIT)
拨号服务器是什么,有什么用处?
C语言中如何“指名道姓”的进行初始化
How to set computer IP?
2022.4.20-----leetcode.388
What are the common proxy IP problems?
Is CICC fortune a state-owned enterprise and is it safe to open an account
搭建网站是用物理机还是云主机好?
Server 2019 the available memory of the server is half of the actual memory
W801 / w800 WiFi socket development (I) - UDP
Batch multiple files into one hex
NPM -- configure Taobao image