numdifftools
The numdifftools library is a suite of tools written in _Python to solve automatic numerical differentiation problems in one or more variables. Finite differences are used in an adaptive manner, coupled with a Richardson extrapolation methodology to provide a maximally accurate result. The user can configure many options like; changing the order of the method or the extrapolation, even allowing the user to specify whether complex-step, central, forward or backward differences are used.
The methods provided are:
- Derivative: Compute the derivatives of order 1 through 10 on any scalar function.
- directionaldiff: Compute directional derivative of a function of n variables
- Gradient: Compute the gradient vector of a scalar function of one or more variables.
- Jacobian: Compute the Jacobian matrix of a vector valued function of one or more variables.
- Hessian: Compute the Hessian matrix of all 2nd partial derivatives of a scalar function of one or more variables.
- Hessdiag: Compute only the diagonal elements of the Hessian matrix
All of these methods also produce error estimates on the result.
Numdifftools also provide an easy to use interface to derivatives calculated with in _AlgoPy. Algopy stands for Algorithmic Differentiation in Python. The purpose of AlgoPy is the evaluation of higher-order derivatives in the forward and reverse mode of Algorithmic Differentiation (AD) of functions that are implemented as Python programs.
Getting Started
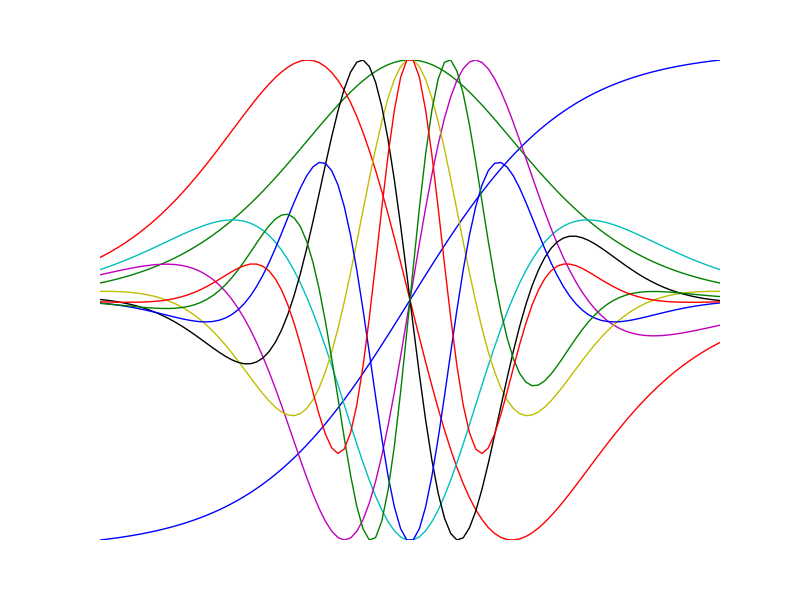
Visualize high order derivatives of the tanh function
>>> import numpy as np >>> import numdifftools as nd >>> import matplotlib.pyplot as plt >>> x = np.linspace(-2, 2, 100) >>> for i in range(10): ... df = nd.Derivative(np.tanh, n=i) ... y = df(x) ... h = plt.plot(x, y/np.abs(y).max())plt.show()
Compute 1'st and 2'nd derivative of exp(x), at x == 1:
>>> fd = nd.Derivative(np.exp) # 1'st derivative >>> fdd = nd.Derivative(np.exp, n=2) # 2'nd derivative >>> np.allclose(fd(1), 2.7182818284590424) True >>> np.allclose(fdd(1), 2.7182818284590424) True
Nonlinear least squares:
>>> xdata = np.reshape(np.arange(0,1,0.1),(-1,1)) >>> ydata = 1+2*np.exp(0.75*xdata) >>> fun = lambda c: (c[0]+c[1]*np.exp(c[2]*xdata) - ydata)**2 >>> Jfun = nd.Jacobian(fun) >>> np.allclose(np.abs(Jfun([1,2,0.75])), 0) # should be numerically zero True
Compute gradient of sum(x**2):
>>> fun = lambda x: np.sum(x**2) >>> dfun = nd.Gradient(fun) >>> np.allclose(dfun([1,2,3]), [ 2., 4., 6.]) True
Compute the same with the easy to use interface to AlgoPy:
>>> import numdifftools.nd_algopy as nda >>> import numpy as np >>> fd = nda.Derivative(np.exp) # 1'st derivative >>> fdd = nda.Derivative(np.exp, n=2) # 2'nd derivative >>> np.allclose(fd(1), 2.7182818284590424) True >>> np.allclose(fdd(1), 2.7182818284590424) True
Nonlinear least squares:
>>> xdata = np.reshape(np.arange(0,1,0.1),(-1,1)) >>> ydata = 1+2*np.exp(0.75*xdata) >>> fun = lambda c: (c[0]+c[1]*np.exp(c[2]*xdata) - ydata)**2 >>> Jfun = nda.Jacobian(fun, method='reverse') >>> np.allclose(np.abs(Jfun([1,2,0.75])), 0) # should be numerically zero True
Compute gradient of sum(x**2):
>>> fun = lambda x: np.sum(x**2) >>> dfun = nda.Gradient(fun) >>> np.allclose(dfun([1,2,3]), [ 2., 4., 6.]) True
See also
scipy.misc.derivative
Documentation and code
Numdifftools works on Python 2.7+ and Python 3.0+.
Official releases available at: http://pypi.python.org/pypi/numdifftools
Official documentation available at: http://numdifftools.readthedocs.io/en/latest/
Bleeding edge: https://github.com/pbrod/numdifftools.
Installation
If you have pip installed, then simply type:
$ pip install numdifftools
to get the lastest stable version. Using pip also has the advantage that all requirements are automatically installed.
Unit tests
To test if the toolbox is working paste the following in an interactive python session:
import numdifftools as nd
nd.test('--doctest-modules', '--disable-warnings')
Acknowledgement
The numdifftools package for Python was written by Per A. Brodtkorb based on the adaptive numerical differentiation toolbox written in Matlab by John D'Errico [DErrico06].
Later the package was extended with some of the functionality found in the statsmodels.tools.numdiff module written by Josef Perktold [JPerktold14] which is based on [Rid09]. The implementation of bicomplex numbers is based on the matlab implementation described in the project report of [Ver14] which is based on [GLD12]. For completeness the [For98] method for computing the weights and points in general finite difference formulas as well as the [For81] method for cumputing the taylor coefficients of complex analytic function using FFT, was added.
References
| [JPerktold14] | Perktold, J (2014), numdiff package http://statsmodels.sourceforge.net/0.6.0/_modules/statsmodels/tools/numdiff.html |
| [Ver14] | Adriaen Verheyleweghen, (2014) "Computation of higher-order derivatives using the multi-complex step method", Project report, NTNU |
| [GLD12] | Gregory Lantoine, R.P. Russell, and T. Dargent (2012) "Using multicomplex variables for automatic computation of high-order derivatives", ACM Transactions on Mathematical Software, Vol. 38, No. 3, Article 16, April 2012, 21 pages, http://doi.acm.org/10.1145/2168773.2168774 |
| [MELEV12] | M.E. Luna-Elizarraras, M. Shapiro, D.C. Struppa1, A. Vajiac (2012), "Bicomplex Numbers and Their Elementary Functions", CUBO A Mathematical Journal, Vol. 14, No 2, (61-80). June 2012. |
| [Lan10] | Gregory Lantoine (2010), "A methodology for robust optimization of low-thrust trajectories in multi-body environments", Phd thesis, Georgia Institute of Technology |
| [Rid09] | Ridout, M.S. (2009) "Statistical applications of the complex-step method of numerical differentiation", The American Statistician, 63, 66-74 |
| [DErrico06] | D'Errico, J. R. (2006), "Adaptive Robust Numerical Differentiation", http://www.mathworks.com/matlabcentral/fileexchange/13490-adaptive-robust-numerical-differentiation |
| [KLLK05] | K.-L. Lai, J.L. Crassidis, Y. Cheng, J. Kim (2005), "New complex step derivative approximations with application to second-order kalman filtering", AIAA Guidance, Navigation and Control Conference, San Francisco, California, August 2005, AIAA-2005-5944. |
| [For98] | B. Fornberg (1998) "Calculation of weights_and_points in finite difference formulas", SIAM Review 40, pp. 685-691. |
| [For81] | Fornberg, B. (1981). "Numerical Differentiation of Analytic Functions", ACM Transactions on Mathematical Software (TOMS), 7(4), 512-526. http://doi.org/10.1145/355972.355979 |
| [JML69] | Lyness, J. M., Moler, C. B. (1969). "Generalized Romberg Methods for Integrals of Derivatives", Numerische Mathematik. |
| [JML66] | Lyness, J. M., Moler, C. B. (1966). "Vandermonde Systems and Numerical Differentiation", Numerische Mathematik. |
| [NAG] | NAG Library. NAG Fortran Library Document: D04AAF |
