当前位置:网站首页>Pytorch learning record (V): back propagation + gradient based optimizer (SGD, adagrad, rmsporp, Adam)
Pytorch learning record (V): back propagation + gradient based optimizer (SGD, adagrad, rmsporp, Adam)
2022-04-23 05:54:00 【Zuo Xiaotian ^ o^】
Back propagation algorithm
The chain rule
Finding partial derivatives

Back propagation

Sigmoid Example of function 




Back propagation algorithm , This is the core of the optimization algorithm in deep learning , Because all gradient based optimization algorithms need to calculate the gradient of each parameter
Variations of various optimization algorithms
Detailed explanation of each parameter of the optimizer :https://www.cnblogs.com/sddai/p/14627785.html
1. Gradient descent method

2.SGD Random gradient descent method
Is to use one batch at a time (batch) Calculate the gradient of the data , Instead of calculating the gradient of all the data .

Formula is : Updated parameter data = Parameter data - Learning rate * Parameter gradient
The code is as follows :
def sgd_update(parameters, lr):
for param in parameters:
param.data = param.data - lr * param.grad.data
Detailed code :
import numpy as np
import torch
from torchvision.datasets import MNIST
from torch.utils.data import DataLoader
from torch import nn
from torch.autograd import Variable
import time
import matplotlib.pyplot as plt
import os
os.environ['KMP_DUPLICATE_LIB_OK'] = 'TRUE'
# batch_size=1 when
# Define data preprocessing functions
def data_tf(x):
x = np.array(x, dtype='float32') / 255 # Change the data to 0-1
x = (x - 0.5) / 0.5 # Standardization
x = x.reshape((-1,)) # Flatten
x = torch.from_numpy(x) # Turn it into Tensor
return x
train_set = MNIST('./data', train=True, transform=data_tf, download=True)
test_set = MNIST('./data', train=False, transform=data_tf, download=True)
# Definition Loss function
criterion = nn.CrossEntropyLoss()
# Define the function of gradient descent
# The formula : Parameter data - Learning rate * gradient
# What is passed in is the parameters of the network , And the learning rate , Output data after gradient descent
def sgd_updata(parameters, lr):
for param in parameters:
param.data = param.data - lr * param.grad.data
# Define the training set
train_data = DataLoader(train_set, batch_size =1, shuffle=True)
# Use Sequential Definition 3 Layer neural networks
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10)
)
# Start training
losses1 = [] # The empty container , cycles
idx = 0 # Training times
start = time.time() # Start timing
for e in range(5):
train_loss = 0 # Initial training loss is 0
for im, label in train_data:
# Read the data in the data , Stored in Variable in
im = Variable(im)
label = Variable(label)
# Forward propagation
out = net(im)
loss = criterion(out, label)
# Back propagation
net.zero_grad() # Gradient clear
loss.backward() # Back propagation
sgd_updata(net.parameters(), 1e-2) # gradient descent , Use 0.01 Learning rate of
# Recording error
train_loss += loss.item()
if idx % 30 == 0:
losses1.append(loss.item())
idx += 1
print('epoch: {}, Train loss: {:.6f}'.format(e, train_loss / len(train_data)))
end = time.time()
print(' Use your time :{:.5f} s'.format(end - start))
# Draw a picture
x_axis = np.linspace(0, 5, len(losses1), endpoint=True)
plt.semilogx(x_axis, losses1, label = 'batch_size=1')
plt.legend(loc='best')
plt.show()

take batch_size Change it to 64

The learning rate is too high, which makes the loss function jump back and forth , Thus, the loss function cannot be reduced better , So we usually use a relatively small learning rate
Pytorch The function that comes with
yes optimzier = torch.optim.SGD(net.parameters(), lr)
The specific form is as follows :
class torch.optim.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)[source]
params (iterable) – Of the parameters to be optimized iterable Or the one that defines the parameter group dict
lr (float) – Learning rate
momentum (float, Optional ) – Momentum factor ( Default :0)
weight_decay (float, Optional ) – Weight falloff (L2 punishment )( Default :0)
dampening (float, Optional ) – The suppressor of momentum ( Default :0)
nesterov (bool, Optional ) – Use Nesterov momentum ( Default :False)
3.Momentum momentum
While the random gradient drops , gaining momentum
The gradient descent can be imagined as a very flat funnel , So in the vertical direction , The gradient is very large , In the horizontal direction , The gradient is relatively small , So when we set the learning rate, we can't set it too large , In order to prevent parameter updating in the vertical direction, too much , Such a small learning rate leads to too slow updating of parameters in the horizontal direction , So it leads to very slow convergence .


pytorch in torch.optim.SGD(net.parameters(), lr=1e-2, momentum=0.9) # Add momentum
import numpy as np
import torch
from torchvision.datasets import MNIST # Import pytorch Built in mnist data
from torch.utils.data import DataLoader
from torch import nn
from torch.autograd import Variable
import time
import matplotlib.pyplot as plt
import os
os.environ['KMP_DUPLICATE_LIB_OK'] = 'TRUE'
def data_tf(x):
x = np.array(x, dtype='float32') / 255
x = (x - 0.5) / 0.5 # Standardization , This technique will be discussed later
x = x.reshape((-1,)) # Flatten
x = torch.from_numpy(x)
return x
train_set = MNIST('./data', train=True, transform=data_tf, download=True) # Loading data sets , Declare the defined data transformation
test_set = MNIST('./data', train=False, transform=data_tf, download=True)
# Definition loss function
criterion = nn.CrossEntropyLoss()
train_data = DataLoader(test_set, batch_size=64, shuffle=True)
# Define the network model
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10)
)
optimizer = torch.optim.SGD(net.parameters(), lr=1e-2, momentum=0.9)
losses = []
idx = 0
start = time.time()
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# Forward propagation
out = net(im)
loss = criterion(out, label)
# Back propagation
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Recording error
train_loss += loss.item()
if idx % 30 == 0: # 30 Step record once
losses.append(loss.item())
idx += 1
print('epoch:{}, Train Loss: {:.6f}'.format(e, train_loss / len(train_data)))
end = time.time()
print(' Use your time :{:.5f} s'.format(end - start))
x_axis = np.linspace(0, 5, len(losses), endpoint=True)
plt.semilogy(x_axis, losses, label='momentum: 0.9')
plt.legend(loc='best')
plt.show()
4.Adagrad Adaptive learning rate (adaptive)

Adagrad My idea is very simple , One at a time batch size When updating the parameters of the data , We need to calculate the gradient of all parameters , So the idea is for each parameter , Initialize a variable s by 0, Then sum the gradient squares of the parameter each time and add them to this variable s On , Then when updating this parameter , The learning rate becomes



Define your own adagrad function :
def sgd_adagrad(parameters, sqrs, lr):
eps = 1e-10
for param, sqr in zip(parameters, sqrs):
sqr[:] = sqr + param.grad.data ** 2
div = lr / torch.sqrt(sqr + eps) * param.grad.data
param.data = param.data - div
pytorch The command optimizer = torch.optim.Adagrad(net.parameters(), lr=1e-2)
import numpy as np
import torch
from torchvision.datasets import MNIST # Import pytorch Built in mnist data
from torch.utils.data import DataLoader
from torch import nn
from torch.autograd import Variable
import time
import matplotlib.pyplot as plt
import os
os.environ['KMP_DUPLICATE_LIB_OK'] = 'TRUE'
def data_tf(x):
x = np.array(x, dtype='float32') / 255
x = (x - 0.5) / 0.5 # Standardization , This technique will be discussed later
x = x.reshape((-1,)) # Flatten
x = torch.from_numpy(x)
return x
train_set = MNIST('./data', train=True, transform=data_tf, download=True) # Loading data sets , Declare the defined data transformation
test_set = MNIST('./data', train=False, transform=data_tf, download=True)
# Definition loss function
criterion = nn.CrossEntropyLoss()
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# Use Sequential Definition 3 Layer neural networks
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)
optimizer = torch.optim.Adagrad(net.parameters(), lr=1e-2)
# Start training
start = time.time() # Time begins
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# Forward propagation
out = net(im)
loss = criterion(out, label)
# Back propagation
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Recording error
train_loss += loss.item()
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # End of the timing
print(' Use your time : {:.5f} s'.format(end - start))
5.RMSprop An improved method of adaptive learning rate

class torch.optim.RMSprop(params, lr=0.01, alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)[source]
Realization RMSprop Algorithm .
from G. Hinton Put forward in his course . The central version first appeared in Generating Sequences With Recurrent Neural Networks.
Parameters :
params (iterable) – Of the parameters to be optimized iterable Or the one that defines the parameter group dict
lr (float, Optional ) – Learning rate ( Default :1e-2)
momentum (float, Optional ) – Momentum factor ( Default :0)
alpha (float, Optional ) – Smoothing constant ( Default :0.99)
eps (float, Optional ) – A term added to the denominator to increase the stability of numerical calculations ( Default :1e-8)
centered (bool, Optional ) – If True, Computing centric RMSProp, And its variance prediction value is used to normalize the gradient
weight_decay (float, Optional ) – Weight falloff (L2 punishment )( Default : 0)
import numpy as np
import torch
from torchvision.datasets import MNIST # Import pytorch Built in mnist data
from torch.utils.data import DataLoader
from torch import nn
from torch.autograd import Variable
import time
import matplotlib.pyplot as plt
import os
os.environ['KMP_DUPLICATE_LIB_OK'] = 'TRUE'
def data_tf(x):
x = np.array(x, dtype='float32') / 255
x = (x - 0.5) / 0.5 # Standardization , This technique will be discussed later
x = x.reshape((-1,)) # Flatten
x = torch.from_numpy(x)
return x
train_set = MNIST('./data', train=True, transform=data_tf, download=True) # Loading data sets , Declare the defined data transformation
test_set = MNIST('./data', train=False, transform=data_tf, download=True)
# Definition loss function
criterion = nn.CrossEntropyLoss()
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# Use Sequential Definition 3 Layer neural networks
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)
optimizer = torch.optim.RMSprop(net.parameters(), lr=1e-3, alpha=0.9)
# Start training
start = time.time() # Time begins
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# Forward propagation
out = net(im)
loss = criterion(out, label)
# Back propagation
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Recording error
train_loss += loss.item()
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # End of the timing
print(' Use your time : {:.5f} s'.format(end - start))
Adam
RMSprop Plus momentum (Momentum)
It's better than RMSProp Better results

pytorch in torch.optim.Adam()
import numpy as np
import torch
from torchvision.datasets import MNIST # Import pytorch Built in mnist data
from torch.utils.data import DataLoader
from torch import nn
from torch.autograd import Variable
import time
import matplotlib.pyplot as plt
import os
os.environ['KMP_DUPLICATE_LIB_OK'] = 'TRUE'
def data_tf(x):
x = np.array(x, dtype='float32') / 255
x = (x - 0.5) / 0.5 # Standardization , This technique will be discussed later
x = x.reshape((-1,)) # Flatten
x = torch.from_numpy(x)
return x
train_set = MNIST('./data', train=True, transform=data_tf, download=True) # Loading data sets , Declare the defined data transformation
test_set = MNIST('./data', train=False, transform=data_tf, download=True)
# Definition loss function
criterion = nn.CrossEntropyLoss()
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# Use Sequential Definition 3 Layer neural networks
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)
optimizer = torch.optim.Adam(net.parameters(), lr=1e-3)
# Start training
start = time.time() # Time begins
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# Forward propagation
out = net(im)
loss = criterion(out, label)
# Back propagation
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Recording error
train_loss += loss.item()
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # End of the timing
print(' Use your time : {:.5f} s'.format(end - start))
Adam As the default optimization algorithm , It can often achieve better results , meanwhile SGD+Momentum The method is also worth trying
Adadelta
pytorch in torch.optim.Adadelta(net.parameters(), rho=0.9)
class torch.optim.Adadelta(params, lr=1.0, rho=0.9, eps=1e-06, weight_decay=0)[source]
Realization Adadelta Algorithm .
It's in ADADELTA: An Adaptive Learning Rate Method. It was proposed that .
Parameters :
params (iterable) – Of the parameters to be optimized iterable Or the one that defines the parameter group dict
rho (float, Optional ) – Coefficient used to calculate the operating average of the square gradient ( Default :0.9)
eps (float, Optional ) – A term added to the denominator to increase the stability of numerical calculations ( Default :1e-6)
lr (float, Optional ) – stay delta The coefficient that is scaled before being applied to the parameter update ( Default :1.0)
weight_decay (float, Optional ) – Weight falloff (L2 punishment )( Default : 0)
版权声明
本文为[Zuo Xiaotian ^ o^]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204230543244175.html
边栏推荐
- 金蝶EAS“总账”系统召唤“反过账”按钮
- Pytorch——数据加载和处理
- 编程记录——图片旋转函数scipy.ndimage.rotate()的简单使用和效果观察
- Pytorch学习记录(十二):学习率衰减+正则化
- Pytorch学习记录(十):数据预处理+Batch Normalization批处理(BN)
- 容器
- 多个一维数组拆分合并为二维数组
- 对比学习论文——[MoCo,CVPR2020]Momentum Contrast for Unsupervised Visual Representation Learning
- Understand the current commonly used encryption technology system (symmetric, asymmetric, information abstract, digital signature, digital certificate, public key system)
- Font shape `OMX/cmex/m/n‘ in size <10.53937> not available (Font) size <10.95> substituted.
猜你喜欢

Multithreading and high concurrency (1) -- basic knowledge of threads (implementation, common methods, state)

Pytorch学习记录(三):神经网络的结构+使用Sequential、Module定义模型

Pyqy5 learning (4): qabstractbutton + qradiobutton + qcheckbox
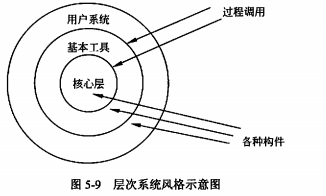
软件架构设计——软件架构风格

Pyqy5 learning (III): qlineedit + qtextedit

域内用户访问域外samba服务器用户名密码错误

Dva中在effects中获取state的值

Pytorch学习记录(十二):学习率衰减+正则化

MySQL realizes master-slave replication / master-slave synchronization

JVM series (3) -- memory allocation and recycling strategy
随机推荐
io.lettuce.core.RedisCommandExecutionException: ERR wrong number of arguments for ‘auth‘ command
Pytorch学习记录(十二):学习率衰减+正则化
解决报错:ImportError: IProgress not found. Please update jupyter and ipywidgets
Write your own redistemplate
多线程与高并发(2)——synchronized用法详解
umi官网yarn create @umijs/umi-app 报错:文件名、目录名或卷标语法不正确
Package mall system based on SSM
POI generates excel and inserts pictures
Dva中在effects中获取state的值
RedHat realizes keyword search in specific text types under the directory and keyword search under VIM mode
Meta annotation (annotation of annotation)
关于二叉树的遍历
Excel obtains the difference data of two columns of data
数字图像处理基础(冈萨雷斯)二:灰度变换与空间滤波
Anaconda
编写一个自己的 RedisTemplate
线程的底部实现原理—静态代理模式
Multithreading and high concurrency (3) -- synchronized principle
protected( 被 protected 修饰的成员对于本包和其子类可见)
Idea plug-in --- playing songs in the background