当前位置:网站首页>Pytorch学习记录(三):神经网络的结构+使用Sequential、Module定义模型
Pytorch学习记录(三):神经网络的结构+使用Sequential、Module定义模型
2022-04-23 05:43:00 【左小田^O^】


例如:
nn.Linear(in,out)
如输入层4个节点,输出2个节点,可以用nn.Linear(4,2)来表示,同时 nn.Linear(in,out,bias=False)可以不使用偏置,默认是True。
N 层神经网络并不会把输入层算进去,
因此一个一层的神经网络是指没有隐藏层、只有输入层和输出层的神经网络。
Logistic回归就是一个一层的神经网络。
输出层一般是没有激活函数的,因为输出层通常表示一个类别的得分或者回归的一个实值的目标,所以输出层可以是任意的实数。
模型的表示能力与容量

上面三张图分别是三个网络模型做二分类得到的结果,每个网络模型都是一个隐藏层,但是每个隐藏层的节点数目不一样,从左到右分别是3个、6个和20个隐藏节点,这三个模型训练之后得到的结果完全不一样,可以看到隐藏节点越多的模型能够表示更加复杂的模型,然而根据我们想要的结果,其实最左边的模型才是最好的,最右边的模型虽然有着更加复杂的形状,但是它忽略了潜在的数据关系,将噪声的干扰放大了,这种效果被称为过拟合(overfitting)。
神经网络的损失函数一般是非凸的,容量小的网络更容易陷入局部极小点而达不到最优的效果,同时这些局部最小点的方差特别大,换句话说,也就是每个局部最优点的差异都特别大,所以你在训练网络的时候训练10次可能得到的结果有很大的差异。但是对于容量更大的神经网络,它的局部极小点的方差特别小,也就是说训练多次虽然可能陷入不同的局部极小点,但是它们之间的差异是很小的,这样训练就不会完全依靠随机初始化。
Sequential 和 Module
**Sequential (序列)**允许我们构建序列化的模块,一个有序的容器,神经网络模块将按照在传入构造器的顺序依次被添加到计算图中执行,同时以神经网络模块为元素的有序字典也可以作为传入参数。
即:用于存放神经网络的各层
# Sequential
seq_net = nn.Sequential(
nn.Linear(2, 4), # PyTorch 中的线性层,wx + b
nn.Tanh(),
nn.Linear(4, 1)
)
# 序列模块可以通过索引访问每一层
seq_net[0] # 第一层
Linear(in_features=2, out_features=4)
# 打印出第一层的权重
w0 = seq_net[0].weight
print(w0)
# 结果
Parameter containing:
-0.4964 0.3581
-0.0705 0.4262
0.0601 0.1988
0.6683 -0.4470
[torch.FloatTensor of size 4x2]
通过 parameters 可以取得模型的参数,直接应用于构造优化器
# 通过 parameters 可以取得模型的参数
param = seq_net.parameters()
# 定义优化器
optim = torch.optim.SGD(param, 1.)
# 我们训练 10000 次
for e in range(10000):
out = seq_net(Variable(x))
loss = criterion(out, Variable(y))
optim.zero_grad()
loss.backward()
optim.step()
if (e + 1) % 1000 == 0:
print('epoch: {}, loss: {}'.format(e+1, loss.data[0]))
结果:
epoch: 1000, loss: 0.2839296758174896
epoch: 2000, loss: 0.2716798782348633
epoch: 3000, loss: 0.2647360861301422
epoch: 4000, loss: 0.26001378893852234
epoch: 5000, loss: 0.2566395103931427
epoch: 6000, loss: 0.2541380524635315
epoch: 7000, loss: 0.25222381949424744
epoch: 8000, loss: 0.2507193386554718
epoch: 9000, loss: 0.24951006472110748
epoch: 10000, loss: 0.2485194206237793
可以看到,训练 10000 次 loss 比之前的更低,这是因为 PyTorch 自带的模块比我们写的更加稳定。
模型的保存
参数是w和b
模型就是定义的seq_net
将参数和模型保存在一起
# 将参数和模型保存在一起
torch.save(seq_net, 'save_seq_net.pth')
torch.save里面有两个参数,第一个是要保存的模型,第二个参数是保存的路径
读取保存的模型
# 读取保存的模型
seq_net1 = torch.load('save_seq_net.pth')
保存模型参数
# 保存模型参数
torch.save(seq_net.state_dict(), 'save_seq_net_params.pth')
如果要重新读入模型的参数,首先我们需要重新定义一次模型,接着重新读入参数
如下;
seq_net2 = nn.Sequential(
nn.Linear(2, 4),
nn.Tanh(),
nn.Linear(4, 1)
)
# 加载参数
seq_net2.load_state_dict(torch.load('save_seq_net_params.pth'))
seq_net2
Sequential(
(0): Linear(in_features=2, out_features=4)
(1): Tanh()
(2): Linear(in_features)
print(seq_net2[0].weight)
Parameter containing:
-0.5532 -1.9916
0.0446 7.9446
10.3188 -12.9290
10.0688 11.7754
[torch.FloatTensor of size 4x2]
通过这种方式我们也重新读入了相同的模型,打印第一层的参数对比,发现和前面的办法是一样有这两种保存和读取模型的方法,推荐使用第二种,因为第二种可移植性更强。
Module(模型) 是一种更加灵活的模型定义方式,我们下面分别用 Sequential 和 Module 来定义上面的神经网络。
使用Module定义的模板
class 网络名字(nn.Module):
def __init__(self, 一些定义的参数):
super(网络名字, self).__init__()
self.layer1 = nn.Linear(num_input, num_hidden)
self.layer2 = nn.Sequential(...)
...
定义需要用的网络层
def forward(self, x): # 定义前向传播
x1 = self.layer1(x)
x2 = self.layer2(x)
x = x1 + x2
...
return x
举例
class module_net(nn.Module):
def __init__(self, num_input, num_hidden, num_output):
super(module_net, self).__init__()
self.layer1 = nn.Linear(num_input, num_hidden) # 输入层
self.layer2 = nn.Tanh() # 激活函数
self.layer3 = nn.Linear(num_hidden, num_output) # 输出层,隐藏层层数要一直,最后输出一个
def forward(self, x):
x = self.layer1(x)
x = self.layer2(x)
x = self.layer3(x)
return x
mo_net = module_net(2, 4, 1)
访问模型中的某层可以直接通过名字
# 访问模型中的某层可以直接通过名字
# 第一层
l1 = mo_net.layer1
print(l1)
Linear(in_features=2, out_features=4)
# 打印出第一层的权重
print(l1.weight)
Parameter containing:
0.1492 0.4150
0.3403 -0.4084
-0.3114 -0.0584
0.5668 0.2063
[torch.FloatTensor of size 4x2]
# 定义优化器
optim = torch.optim.SGD(mo_net.parameters(), 1.)
# 我们训练 10000 次
for e in range(10000):
out = mo_net(Variable(x))
loss = criterion(out, Variable(y))
optim.zero_grad()
loss.backward()
optim.step()
if (e + 1) % 1000 == 0:
print('epoch: {}, loss: {}'.format(e+1, loss.data[0]))
epoch: 1000, loss: 0.2618132531642914
epoch: 2000, loss: 0.2421271800994873
epoch: 3000, loss: 0.23346386849880219
epoch: 4000, loss: 0.22809192538261414
epoch: 5000, loss: 0.224302738904953
epoch: 6000, loss: 0.2214415818452835
epoch: 7000, loss: 0.21918588876724243
epoch: 8000, loss: 0.21736061573028564
epoch: 9000, loss: 0.21585838496685028
epoch: 10000, loss: 0.21460506319999695
# 保存模型
torch.save(mo_net.state_dict(), 'module_net.pth')
版权声明
本文为[左小田^O^]所创,转载请带上原文链接,感谢
https://blog.csdn.net/qq_45802081/article/details/119893427
边栏推荐
- MySql基础狂神说
- 手动删除eureka上已经注册的服务
- 基于thymeleaf实现数据库图片展示到浏览器表格
- io. lettuce. core. RedisCommandExecutionException: ERR wrong number of arguments for ‘auth‘ command
- The difference between cookie and session
- JVM系列(3)——内存分配与回收策略
- MySQL query uses \ g, column to row
- Strategies to improve Facebook's touch rate and interaction rate | intelligent customer service helps you grasp users' hearts
- Step on the pit: Nacos uses startup CMD - M standalone startup error
- mysql如何将存储的秒转换为日期
猜你喜欢

Manually delete registered services on Eureka
基于ssm 包包商城系统

Pilotage growth · ingenuity empowerment -- yonmaster developer training and pilotage plan is fully launched

Flutter 新一代圖形渲染器 Impeller

框架解析1.系统架构简介

JVM系列(4)——内存溢出(OOM)

AcWing 836. Merge set (merge set)
jdbc入门\获取数据库连接\使用PreparedStatement
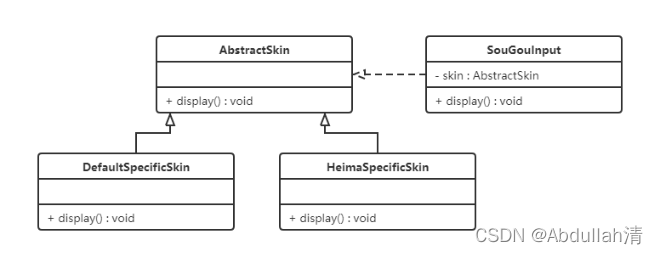
2 - principes de conception de logiciels

PyQy5学习(三):QLineEdit+QTextEdit
随机推荐
rsync实现文件服务器备份
实体中list属性为空或者null,设置为空数组
poi导出excel,行相同数据自动合并单元格
Common status codes
SQL注入
‘EddiesObservations‘ object has no attribute ‘filled‘
interviewter:介绍一下MySQL日期函数
Find the number of "blocks" in the matrix (BFS)
RedHat6之smb服务访问速度慢解决办法记录
mysql-触发器、存储过程、存储函数
类的加载与ClassLoader的理解
Mysql 查询使用\G,列转行
Add days to date
一文读懂当前常用的加密技术体系(对称、非对称、信息摘要、数字签名、数字证书、公钥体系)
第36期《AtCoder Beginner Contest 248 打比赛总结》
MySQL query uses \ g, column to row
Map对象 map.get(key)
Differences between sea level anatomy and sea surface height anatomy
MySQL创建oracle练习表
Latex快速入门