当前位置:网站首页>基于Qiskit——《量子计算编程实战》读书笔记(七)
基于Qiskit——《量子计算编程实战》读书笔记(七)
2022-08-10 05:29:00 【溴锑锑跃迁】
第11章 量子傅里叶变换
经典傅里叶变换
在开始傅里叶变换之前,我希望读者能回忆一下线性空间这一概念:
-UP主汉语配音-【线性代数的本质】合集-转载于3Blue1Brown官方双语】
上面分享的视频是关于线性组合、张成的空间和基的。利用一点点高中知识,我们知道通过平面向量基本定理可以在一个平面内用任意两个不平行的向量去表示这一平面内的所有向量,或者我们还可以说,仅仅通过两个向量,我们实际上可以定义一个平面。
如果有:
那么就有:
其中 的条件就是为了保证两向量不平行,因为一旦平行,就说明两个向量可以相互表示(或者说仅仅长度有区别,方向毫无区别!),那么我们就无法表示某一平面上的任意向量了。我们称如前所述的这些两两间无法相互表示的向量称为线性无关的向量组,某种意义上,它们也是相互独立的。关于线性无关或者是独立最简单的验证方法,就是观察是否存在某一个不为零的常数λ使得
的条件就是为了保证两向量不平行,因为一旦平行,就说明两个向量可以相互表示(或者说仅仅长度有区别,方向毫无区别!),那么我们就无法表示某一平面上的任意向量了。我们称如前所述的这些两两间无法相互表示的向量称为线性无关的向量组,某种意义上,它们也是相互独立的。关于线性无关或者是独立最简单的验证方法,就是观察是否存在某一个不为零的常数λ使得 ,如果不存在,那么两个矢量就是线性无关的。
,如果不存在,那么两个矢量就是线性无关的。
接下来让我们将这个概念扩充到函数当中,我们定义如果不存在一个非零常数λ使得 恒成立,则称两函数线性无关。那么两矢量线性无关可以张成一个平面,两函数线性无关有什么数学意义吗?答案就是,你可以通过这两个函数构造、表示很多其他函数!如果两函数线性相关,那么再怎么折腾这两个函数,不过是放大或缩小了其中一个函数罢了。
恒成立,则称两函数线性无关。那么两矢量线性无关可以张成一个平面,两函数线性无关有什么数学意义吗?答案就是,你可以通过这两个函数构造、表示很多其他函数!如果两函数线性相关,那么再怎么折腾这两个函数,不过是放大或缩小了其中一个函数罢了。
类比来看,我们可以在某种程度上称一组线性无关的函数为一组线性无关的向量!故而,为了充分表示数学界各式各样的函数,我们需要的可能不止两个函数,况且,一谈及数学,无穷也应当被纳入我们的考虑范围。于是,傅里叶变换变横空出世!
傅里叶变换的精髓在于各式各样的正弦函数,我们知道,最普泛的正弦函数可以被写成以下形式:

通过调节A、f、φ三个参数,我们实际上获得任意正弦函数,而这恰好符合了我们的要求!
编写任意正弦函数作图函数如下:
import numpy as np
import matplotlib.pyplot as plot
def plot_wave(A,f,phi,name='',color='g'):
plot.clf()
x = np.arange(0, 1, 0.01);
y = A*np.sin(2*np.pi*f*x + np.pi/180*phi)
plot.plot(x,y)
plot.xlabel('x')
plot.ylabel('y')
plot.title(name)
plot.grid(True, which='both')
plot.axhline(y=0, color='k')
plot.show()
plot_wave(1,1,0,'sine wave, A=1, f=1, $\phi=0^{\circ}$')
plot_wave(1,1,90,'cosine wave, A=1, f=1, $\phi=90^{\circ}$')成果图:

现在让我们编写制备正弦波的函数并借此制备两个正弦波(以下简称波):
sampling_rate = 100 # 每秒采样量或说采样速率
time_interval=2 # 采样时间
n_samples = int(sampling_rate*time_interval) # 给定参数情况下的总采样量
def wave(A,f,phi):
"""
x是一个存储从0到T上每个采样区间上采集n_samples长的样本的数组
y是一个存储x对应函数值的数组"""
sampling_interval = 1/sampling_rate # 两样本间的距离
x = np.arange(0, time_interval, sampling_interval);
y = A*np.sin(2*np.pi*f*x + np.pi/180*phi)
return ygreen_wave=wave(10,0.5,0)
blue_wave=wave(0.75,15,90)如果我们定义:red_wave = green_wave + blue_wave,则意味着我们在叠加两个波!接下来,我们将使用傅里叶变换将red_wave拆解回green_wave和blue_wave。那么有同学就问了,你既然都知道red_wave = green_wave + blue_wave,反向拆解岂不是很简单吗?其实我们可以这样想,1+3可以等于4,2+2也可以等于4,但如果反向推出4是由3+1而非2+2得出的,则就不那么容易了,再生活化一点,你把各种颜色的颜料放到一起,然而要想重新分开各种颜色,则也就不那么容易了。
代码如下:
red_wave=green_wave+blue_wave
from numpy import fft # 注意要引用numpy中的fft包进行傅里叶变换
fft_wave = fft.fft(red_wave)/n_samples # 计算并正则化FFT
frequencies_tried=np.arange(n_samples)/time_interval #尝试各种频率
amplitude=2*np.absolute(fft_wave) # 只截取“频率”的前半部分,因为后半部分
# 是前半部分表示冗余信息的复共轭,所以我们的
# 频率实际上差了一半,我们通过乘2来补全
half_range=range(int(n_samples/2)) # 请记住,我们只需要讨论范围的一半
for f,a in zip(frequencies_tried[half_range],amplitude[half_range]):
if a>1e-6: # 忽略过小的系数,因为它仅仅是数值误差
print("the amplitude at f=%.2f is A=%.2f"%(f,a))结果:
![]()
附注:
- 代码中出现的zip函数是用两个等长数组来构建元组数组的,详情请见Python zip() 函数 | 菜鸟教程 (runoob.com)
- 如上所述,我们使用傅里叶的目的是将函数(这里用函数值的分立值代替)拆解为原有的成分。大体来说,傅里叶变换可分为连续和离散两种,连续意味着使用原始的函数,这只在数学理论上是可行的,因为对于任何操作系统来说,都必须对函数进行分立求值,也就是对函数的一部分进行采样。
- 傅里叶变换的原理:fft会尝试尽各种频率的正弦函数,并确定其在母函数中的份量(该份量可以用放缩振幅来表示,例如sin(5x)份量很大,我们就对应地要乘一个很大的数,反之亦然)
量子傅里叶变换
量子傅里叶变换执行类似的操作,它不是对数据执行离散傅里叶变换,而是对量子态本身进行离散傅里叶变换。本文仍不提供量子傅里叶变换的数学细节,而是给出其实现电路及其所需背景。
量子傅里叶变换的实现
为实现量子傅里叶变换,我们需要哈达玛门、自定义的新门以及交换门(SWAP)。
新定义的门被称为旋转门 ,它是一种受控门,意味着会有控制位和目标位。回忆第三章中学习的S门的矩阵定义:
,它是一种受控门,意味着会有控制位和目标位。回忆第三章中学习的S门的矩阵定义:
S = np.matrix([[1, 0], [0, np.e**(i_*np.pi/2.)]])而S的物理意义或说几何意义是沿z轴绕x-y平面旋转90°( 弧度)。类似地,我们可以定义这样一个函数:
弧度)。类似地,我们可以定义这样一个函数:
def rotation(lambda):
return np.matrix([[1,0][0,np.e**(i_*lambda)]]) 那么就代表沿z轴绕x-y平面旋转λ弧度。于是我们定义 :
:
def Rk(k):
return np.matrix([[1,0][0,np.e**(2*np.pi*1j/2**k)]])等价于说(注意e上的指数):

实际上也意味着将360°分成了 份!其中k代指索引(详见下面电路原理)。
份!其中k代指索引(详见下面电路原理)。
接下来,就是仿照CNOT门的结构使之成为一个受控门:
def CRk(k):
return np.matrix([[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,np.e**(2*np.pi*1j/2**k)]])然后是反向门,在两个量子比特的条件下,反向门的操作如下表:
| 输入 | 输出 |
| 00 | 00 |
| 01 | 01 |
| 10 | 01 |
| 11 | 11 |
也就是说,如果第一位为1,则调换两个量子比特。其表示符号是跨过电路的每条导线的交叉点:

量子傅里叶变换电路
对于第一个量子比特,量子傅里叶变换(QFT)电路工作方式如下:
- 在第一个量子比特上应用哈达玛门;
- 使用参数k=2将
 应用于第一个量子比特,目标位是第二个量子比特;
应用于第一个量子比特,目标位是第二个量子比特; - 继续对第k个量子比特使用
 ,但每次k加一,也就是说下一次是对第二个量子比特使用k=3时的
,但每次k加一,也就是说下一次是对第二个量子比特使用k=3时的 ,直到用尽量子比特。
,直到用尽量子比特。
三个量子比特时的QFT电路如图所示(留意U门的第一个参数):
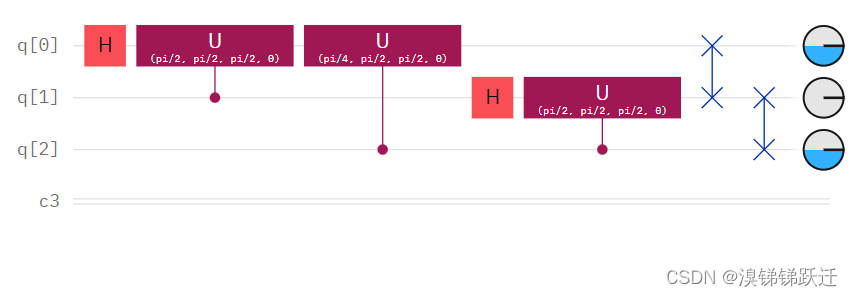
代码如下(由IBMQ平台自动生成):
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit
from numpy import pi
qreg_q = QuantumRegister(3, 'q')
creg_c = ClassicalRegister(3, 'c')
circuit = QuantumCircuit(qreg_q, creg_c)
circuit.h(qreg_q[0])
circuit.cu(pi / 2, pi / 2, pi / 2, 0, qreg_q[1], qreg_q[0])
circuit.cu(pi / 4, pi / 2, pi / 2, 0, qreg_q[2], qreg_q[0])
circuit.h(qreg_q[1])
circuit.cu(pi / 2, pi / 2, pi / 2, 0, qreg_q[2], qreg_q[1])
circuit.swap(qreg_q[0], qreg_q[1])
circuit.swap(qreg_q[1], qreg_q[2])最后我们需要对算法进行泛化至n个量子比特:
def qft(qr,qc,n_qubits):
for i in range(n_qubits):
for j in range(i):
qc.cu(numpy.pi/float(2**(i-j)), numpy.pi/2, 0, qr[i], qr[j])
qc.h(qr[i])由于是读书笔记,内容结构都仿照了原书,更为深入透彻的讲解详见另一文章。
边栏推荐
猜你喜欢

AVL tree insertion--rotation notes

awk of the Three Musketeers of Shell Programming

如何在报表控件FastReport.NET中连接XLSX 文件作为数据源?

【LeetCode】41、 缺失的第一个正数

mysql常用命令有什么

Interface debugging also can play this?

最强大脑(1)

Conda creates a virtual environment method and pqi uses a domestic mirror source to install a third-party library method tutorial

MySQL使用简单教程

【裴蜀定理】CF1055C Lucky Days
随机推荐
Matlab simulation of multi-factor house price prediction based on BP neural network
Become a language that hackers have to learn. Do you think it's okay after reading it?
看了几十篇轻量化目标检测论文扫盲做的摘抄笔记
Error when installing oracle rac 11g and executing root.sh
flex 相关
Read the excerpt notes made by dozens of lightweight target detection papers for literacy
大咖说·对话生态|当Confluent遇见云:实时流动的数据更有价值
剑指Offer 033.变位数组
[Thesis Notes] Prototypical Contrast Adaptation for Domain Adaptive Semantic Segmentation
How to use Apifox's Smart Mock function?
并发工具类——CountDownLatch、CyclicBarrier、Semaphore、Exchanger的介绍与使用
EasyGBS connects to mysql database and prompts "can't connect to mysql server", how to solve it?
Attention candidates for the soft exam! The detailed registration process for the second half of 2022 is coming!
线程(上篇):线程的创建
基于BP神经网络的多因素房屋价格预测matlab仿真
通过一个案例轻松入门OAuth协议
咨询cdc 2.0 for mysql不执行flush with read lock.怎么保证bin
软考考生注意!2022年下半年报名详细流程来了!
每周推荐短视频:探索AI的应用边界
FPGA engineer interview questions collection 11~20