当前位置:网站首页>01 knapsack problem (template)
01 knapsack problem (template)
2022-04-22 05:47:00 【lxt1101】
01 Backpack is to give you a backpack , Tell you the capacity of your backpack , There are a number of items , Each item has its own weight and value , There is only one item per item , Ask how to choose to maximize the value of the backpack

#include<iostream>
using namespace std;
#define N 6
#define W 21
int B[N][W] = { 0 };// Initialize to 0 N Subscript indicating whether to steal items ,W It means the capacity of the backpack
// This two-dimensional array finally calculates money n Items , Capacity of w The greatest value a backpack can hold
int w[6] = { 0,2,3,4,5,9 };// The weight of the article
int v[6] = { 0,3,4,5,8,10 };// The value of the goods
void knapsack() {
int k, c;//k It means the first one k A commodity c It means the capacity of the backpack
for (k = 1; k <= N; k++) {
for (c = 1; c <= W; c++) {
if (w[k] > c) {// The current item weighs more than it can hold first
B[k][c] = B[k - 1][c];
}
else {
int value1 = B[k - 1][c - w[k]] + v[k];// steal , Subtract one from the subscript , Capacity minus the weight of the item Express B[k - 1][c - w[k]] The greatest value
int value2 = B[k - 1][c];// Don't steal , Subtract one from the subscript , The capacity doesn't change
if (value1 > value2) {
B[k][c] = value1;
}
else {
B[k][c] = value2;
}
}
}
}
}
int main() {
knapsack();
cout << B[5][20] << endl;// This is equivalent to the first five items , The maximum capacity is 20 What is the maximum value of your backpack
return 0;
}Reference resources : The first month lights lanterns
Rolling array optimization
It can be found by observation that , The answers that can be obtained above are more widespread , for example : Be able to input any previous n Items in w Maximum value at capacity , But the two-dimensional space overhead of arrays is huge , And we don't need any answers , Generally, the data we input will use , So which of the previous answers are superfluous for us , You can reduce the dimension of a two-dimensional array to a one-dimensional array
A binary array :dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])
One dimensional array rolling optimization :
State transition equation :dp[j]=max(dp[j],dp[j-w[i]]+v[i])
// Reverse cycle
The reason for traversing backwards : As can be seen from the recurrence formula above , The two digit result is related to the data in the previous line , Scrolling array optimization has no rows , If positive order , The previous data can have been changed many times , It's not what we want anymore
//dp[j]: amount to dp[i-1][j]
//dp[j-c[i]]: amount to dp[i-1][j-w[i]]
Why reverse order? Please see 0-1 knapsack : Why enumerate in reverse order when using a scrolling array _aidway The column -CSDN Blog
#include<iostream>
#include<algorithm>
using namespace std;
/*
A binary array :dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])
One dimensional array rolling optimization :
State transition equation :dp[j]=max(dp[j],dp[j-w[i]]+v[i])
*/
int w;// Backpack Capacity
int dp[20010];
int n;//n Each item
int wi, vi;//wi weight ,vi value
int main() {
cin >> w >> n;
for (int i = 1; i <= n; i++) {
// Reverse cycle
//dp[j]: amount to dp[i-1][j]
//dp[j-c[i]]: amount to dp[i-1][j-w[i]]
cin >> wi >> vi;
for (int j = w; j >= wi; j--) {
// The two states of each item, selected and unselected
dp[j] = max(dp[j], dp[j - wi] + vi);
}
}
cout << dp[w] << endl;
return 0;
}版权声明
本文为[lxt1101]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204220535140933.html
边栏推荐
猜你喜欢
随机推荐
AcWing 1096. 地牢大师(三维 BFS)代码详细注释
《PyTorch深度学习实践》Lecture_11 卷积神经网络进阶 Convolutional Neural Network
opencv 使用 forEach 像素遍历(pixel 和 const int* position参数都有介绍)
Usage of JSON type field in MySQL
Program compilation (preprocessing operation) + link
JVM探究
Cytoscape安装教程
My common development software
数据挖掘——数据预处理
Data mining -- decision tree classification
10.Advance Next Round
字典树模板
excel的相对引用和绝对引用
机器学习——用鸢尾花数据集画P-R曲线和ROC曲线
【机器学习】Scikit-learn介绍
ThreadLocal.ThreadLocalMap分析
IDEA值得推荐的20款优秀的插件
1.计算a+b
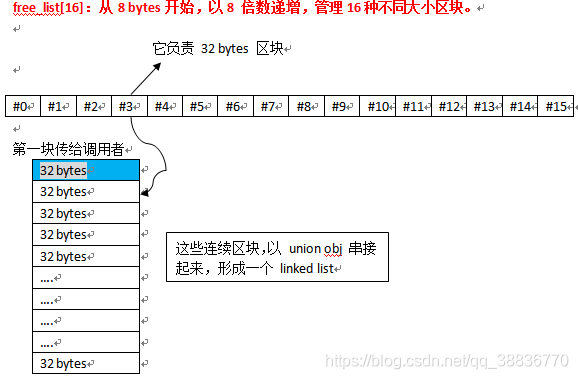
stl alloc 空间分配器 代码解析
Judge whether there are links in the linked list