树结构——2-3树图解

活动地址：CSDN21天学习挑战赛

学习2-3树原理是为了大家后面学习红黑树，B树打好坚实的基础，也能让我们更好的理解和学习。

原理：

2-3树是最简单的B-树（或-树）结构，其每个非叶节点都有两个或三个子女，而且所有叶都在统一层上。2-3树不是二叉树，其节点可拥有3个孩子。不过，2-3树与满二叉树相似。高为h的2-3树包含的节点数大于等于高度为h的满二叉树的节点数，即至少有2^h-1个节点。

这就是一个2-3树。一颗2-3树应该是这样的：

1. 满足二叉树的基本性质
2. 节点可以存放一个或两个元素

2节点：

3节点： 

正是因为每个节点有2个或3个孩子，所以才叫2-3树。

所谓的2-3树满足二叉树的基本性质是指：在2-3树中，2节点的左孩子小于根节点，右孩子大于根节点；3节点的左孩子小于根节点的第一个元素，中间孩子的大小在两个根节点元素之间，右孩子元素大于根节点的第二个元素。

以刚才的图为例：

2节点 ：左孩子 < a < 右孩子
3节点 ：左孩子 < b < 中间孩子 < c < 右孩子
2-3树的绝对平衡

2-3树是一颗绝对平衡的树，所谓的绝对平衡是指在2-3树中从根节点到任意叶子结点所经过的节点数是一样的。

为了保持2-3树的绝对平衡，在元素插入时有以下特征：

如果插入位置节点的父节点的左右孩子都为空，则就和父节点进行融合
如果和一个三节点的节点融合，则可以先融合成四节点，四节点在拆分为以中间大小元素为根，较小元素为中间大小元素的左孩子，较大元素为中间大小元素的右孩子二叉树。若这颗二叉树的根不为2-3树的根，这需要将这个二叉树的根向上融合。

下面我使用图解的方式来让大家了解2-3树：
 

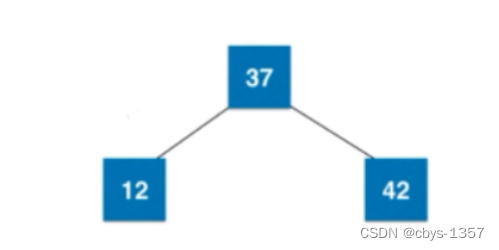
 12应该插入到37左孩子位置，但37节点左右孩子均为空，因此需要进行融合，此时就是和一个3节点进行融合，可以先融合成一个4节点

由于2-3树中只能是2节点或3节点，所以还需要将4节点拆分出来，拆分成以中间大小元素为根，较小元素为中间大小元素的左孩子，较大元素为中间大小元素的右孩子二叉树。即： 

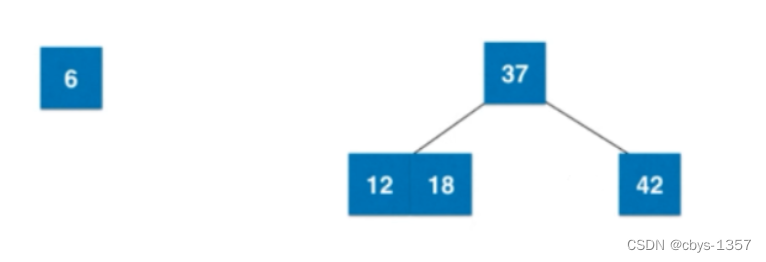
 6应该和12 18 所在的三节点融合，构成一个临时的四节点：

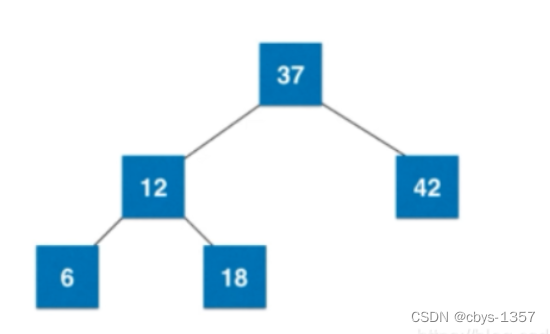
此时需要将4节点拆分： 

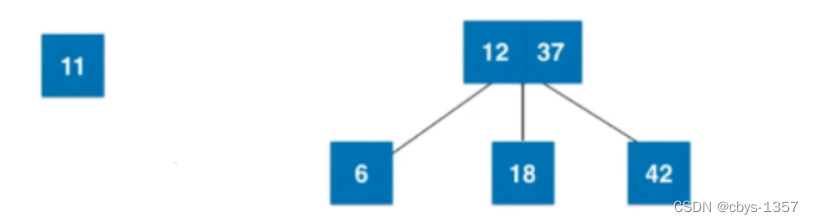
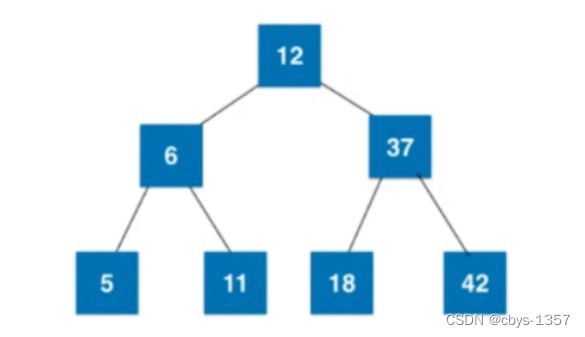
 以这种方式从根结点到任何叶子结点，保持下去整个2-3树保持绝对平衡。