当前位置:网站首页>优先队列
优先队列
2022-08-10 05:32:00 【cbys-1357】

public class MaxPriorityQueue<T extends Comparable<T>> {
//存储堆中的元素
private T[] items;
//记录堆中元素的个数
private int N;
public MaxPriorityQueue(int capacity){
this.items=(T[]) new Comparable[capacity+1];
this.N=0;
}
// 判断堆中索引i处的元素是否小于索引j处的元素
private boolean less(int i,int j) {
return items[i].compareTo(items[j])<0;
}
// 交换元素
private void exch(int i,int j) {
T tmp=items[i];
items[i]=items[j];
items[j]=tmp;
}
// 判断堆中的元素是否为空
public boolean isEmpty() {
return this.N==0;
}
// 返回堆中元素个数
public int size() {
return this.N;
}
// 往堆中插入一个元素
public void insert(T t) {
items[++N]=t;
swim(N);//让元素t上浮
}
// 使用上浮算法,使索引k处的元素能在堆中处于一个正确的位置
private void swim(int k) {
//如果已经到了根结点,就不需要循环了
while(k>1) {
//比较当前结点和其父结点
if(less(k/2,k)) {
//父结点小于当前结点,需要交换
exch(k/2,k);
}
k=k/2;
}
}
//删除堆中最大的元素,并返回这个最大元素
public T delMax() {
T max=items[1];
//交换当前结点和其父结点
exch(1,N);
//删除最后位置上的元素
items[N]=null;
//个数-1
N--;
sink(1);
return max;
}
//使用下沉算法,使索引k处的元素能在堆中处于一个正确的位置
private void sink(int k) {
//如果当前已经是最底层了,就不需要循环了
while(2*k<=N) {
//找到子结点中的较大者
int max;
//若右子结点存在,找到子结点最大值
if(2*k+1<=N) {
if(less(2*k,2*k+1)) {
max=2*k+1;
}else {//右结点不存在,直接将左结点点赋值给最大值
max=2*k;
}
}else {
max=2*k;
}
//比较当前结点和子结点中的较大者,如果当前结点不小,则结束循环
if(!less(k,max)) {
break;
}
//当前结点小,则交换,
exch(k,max);
k=max;
}
}
}
测试类:
public class MaxPriorityQueueTest {
public static void main(String[] args) {
MaxPriorityQueue<String> queue=new MaxPriorityQueue<String>(8);
queue.insert("f");
queue.insert("g");
queue.insert("j");
queue.insert("c");
queue.insert("m");
queue.insert("a");
queue.insert("q");
queue.insert("t");
String s;
while(!queue.isEmpty()) {
s=queue.delMax();
System.out.print(s+"\t");
}
}
}
2.最小优先队列
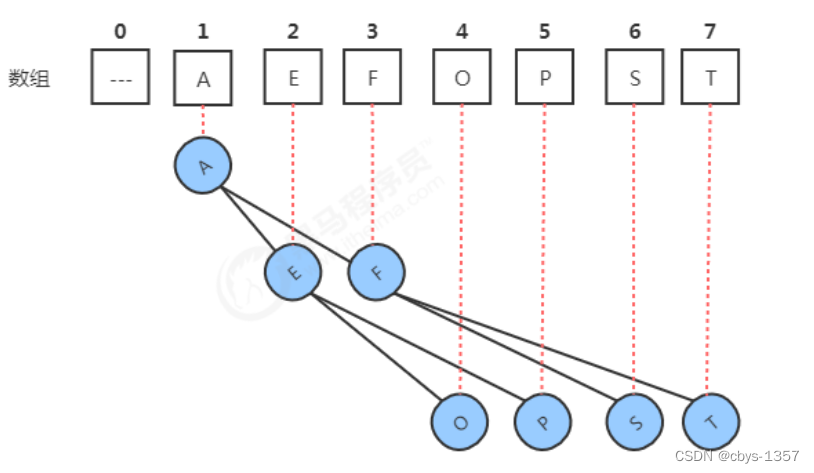
代码实现:
public class MinPriorityQueue<T extends Comparable<T>> {
//存储堆中的元素
private T[] items;
//记录堆中元素的个数
private int N;
// 构造方法
public MinPriorityQueue(int capacity) {
this.items=(T[]) new Comparable[capacity+1];
this.N=0;
}
//判断堆中索引i处的元素是否小于索引j处的元素
private boolean less(int i,int j) {
return items[i].compareTo(items[j])<0;
}
// 交换元素
private void exch(int i,int j) {
T tmp=items[i];
items[i]=items[j];
items[j]=tmp;
}
// 判断堆中的元素是否为空
public boolean isEmpty() {
return this.N==0;
}
// 返回堆中元素个数
public int size() {
return this.N;
}
// 往堆中插入一个元素
public void insert(T t) {
items[++N]=t;
swim(N);
}
//使用上浮算法,使索引k处的元素能在堆中处于一个正确的位置
private void swim(int k) {
//如果没有父结点,则不再上浮
while(k>1) {
//如果当前结点比父结点小,则交换
if(less(k,k/2)) {
exch(k,k/2);
}
k=k/2;
}
}
//删除堆中最小的元素,并返回这个最小元素
public T delMin() {
//索引1处的值是最小值
T min=items[1];
//交换索引1处和索引N处的值
exch(1,N);
//删除索引N处的值
items[N]=null;
//数据元素-1
N--;
//对索引1处的值做下沉,使堆重新有序
sink(1);
//返回被删除的值
return min;
}
//使用下沉算法,使索引k处的元素能在堆中处于一个正确的位置
private void sink(int k) {
//如果没有子结点,则不再下沉
while(2*k<=N) {
//找出子结点中的较小值的索引
int min;
if(2*k+1<=N) {
if(less(2*k,2*k+1)) {
min=2*k;
}else {
min=2*k+1;
}
}else {
min=2*k;
}
//如果当前结点小于子结点中的较小值,则结束循环
if(!less(min,k)) {
break;
}
//当前结点大,交换
exch(min,k);
k=min;
}
}
}
测试代码:
public class MaxPriorityQueueTest {
public static void main(String[] args) {
MaxPriorityQueue<String> queue=new MaxPriorityQueue<String>(8);
queue.insert("f");
queue.insert("g");
queue.insert("j");
queue.insert("c");
queue.insert("m");
queue.insert("a");
queue.insert("q");
queue.insert("t");
String s;
while(!queue.isEmpty()) {
s=queue.delMax();
System.out.print(s+"\t");
}
}
}




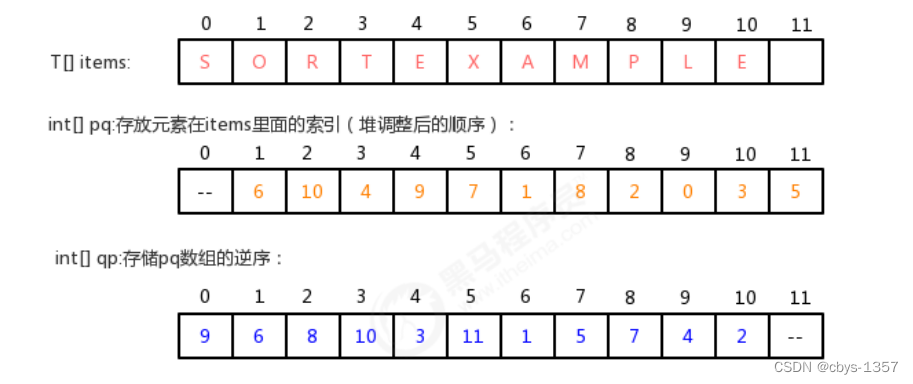
public class IndexMinPriorityQueue<T extends Comparable<T>> {
//存储堆中的元素
private T items[];
//保存每个元素在items数组中的索引,pq数组需要堆有序
private int pq[];
//保存qp的逆序,pq的值作为索引,pq的索引作为值
private int qp[];
//记录堆中元素的个数
private int N;
//构造方法
public IndexMinPriorityQueue(int capacity) {
this.items=(T[]) new Comparable[capacity+1];
this.pq=new int[capacity+1];
this.qp=new int[capacity+1];
this.N=0;
for(int i=0;i<qp.length;i++) {
qp[i]=-1;
}
}
//获取队列中元素的个数
public int size() {
return this.N;
}
//判断队列是否为空
public boolean isEmpty() {
return this.N==0;
}
//判断堆中索引i处的元素是否小于索引j处的元素
private boolean less(int i,int j) {
return items[pq[i]].compareTo(items[pq[j]])<0;
}
//交换堆中i索引和j索引处的值
private void exch(int i,int j) {
//先交换pq数组中的值
int tmp=pq[i];
pq[i]=pq[j];
pq[j]=tmp;
//更新qp数组中的值
qp[pq[i]]=i;
qp[pq[j]]=j;
}
//判断k对应的元素是否存在
public boolean contains(int k) {
return qp[k]!=-1;
}
//最小元素关联的索引
public int minIndex() {
//pq的索引1处,存放的是最小元素在items中的索引
return pq[1];
}
//往队列中插入一个元素,并关联索引i
public void insert(int i,T t) {
//如果索引i处已经存在了元素,则不让插入
if(contains(i)) {
throw new RuntimeException("该索引已经存在");
}
//个数+1
N++;
//把元素存放到items数组中
items[i]=t;
//使用pq存放i这个索引
pq[N]=i;
//在qp的i索引处存放N
qp[i]=N;
//上浮items[pq[N]],让pq堆有序
swim(N);
}
//删除队列中最小的元素,并返回该元素关联的索引
public int delMin() {
//找到items中最小元素的索引
int minIndex=pq[1];
//交换pq中索引1处的值和N处的值
exch(1,N);
//删除qp中索引pq[N]处的值
qp[pq[N]]=-1;
//删除pq中索引N处的值
pq[N]=-1;
//删除items中的最小元素
items[minIndex]=null;
//元素数量-1
N--;
//对pq[1]做下沉,让堆有序
sink(1);
return minIndex;
}
//删除索引i关联的元素
public void delete(int i) {
//找出i在pq中的索引
int k=qp[i];
//把pq中索引k处的值和索引N处的值交换
exch(k,N);
//删除qp中索引pq[N]处的值
qp[pq[N]]=-1;
//删除pq中索引N处的值
pq[N]=-1;
//删除items中索引i处的值
items[k]=null;
//元素数量-1
N--;
//对pq[k]做上浮,让堆有序
swim(k);
//对pq[k]做下沉,让堆有序
sink(k);
}
//把与索引i关联的元素修改为为t
public void changeItem(int i,T t) {
//修改items数组中索引i处的值为t
items[i]=t;
//找到i在pq中的位置
int k=qp[i];
//对pq[k]做上浮,让堆有序
swim(k);
//对pq[k]做下沉,让堆有序
sink(k);
}
//使用上浮算法,使索引k处的元素能在堆中处于一个正确的位置
private void swim(int k) {
//如果已经到了根结点,则结束上浮
while(k>1) {
//比较当前结点和父结点,如果当前结点比父结点小,则交换位置
if(less(k,k/2)) {
exch(k,k/2);
}
k=k/2;
}
}
//使用下沉算法,使索引k处的元素能在堆中处于一个正确的位置
private void sink(int k) {
//如果当前结点已经没有子结点了,则结束下沉
while(2*k<=N) {
//找出子结点中的较小值
int min;
if(2*k+1<=N) {
if(less(2*k,2*k+1)) {
min=2*k;
}else {
min=2*k+1;
}
}else {
min=2*k;
}
//如果当前结点的值比子结点中的较小值小,则结束下沉
if(less(k,min)) {
break;
}
exch(min,k);
k=min;
}
}
}
边栏推荐
猜你喜欢

集合 Map
定时器(setInterval)的开启与关闭

One step ahead, don't miss it again, the chain reading APP will be launched soon!

ORACLE system table space SYSTEM is full and cannot expand table space problem solving process
在yolov5的网络结构中添加注意力机制模块
Index Notes【】【】

链读好文:Jeff Garzik 推出 Web3 制作公司

链读精选:星巴克着眼于数字收藏品并更好地吸引客户

深度学习模型训练前的必做工作:总览模型信息

使用Tenserboard可视化深度学习训练过程
随机推荐
One step ahead, don't miss it again, the chain reading APP will be launched soon!
训练集Loss收敛,但是测试集Loss震荡的厉害?
网络安全5
2021-06-22
shell脚本中利用sqlplus操作数据库
去中心化和p2p网络以及中心化为核心的传统通信
每天一个小知识点
tinymce富文本编辑器
来亲自手搭一个ResNet18网络
事务、存储引擎
笔记1
IO流【】【】【】
win12 modify dns script
用Pytorch从0到1实现逻辑回归
三维点云分割
网络安全3
作业实验四
先人一步,不再错过,链读APP即将上线!
Minio分布式存储系统
智能合约和去中心化应用DAPP
