当前位置:网站首页>【图形学】08 3D坐标系的变换(一)
【图形学】08 3D坐标系的变换(一)
2022-08-08 06:25:00 【纸境止境】
1、流程中图片的变换
世界变换 -> 摄像机变换 ->投影变换 ->视口变换![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zEzidd3x-1658471090944)(assets/image-20220521160840535.png)]](/img/81/1d711c91aeff7cc9d04b1cd12fa5be.png)
2、摄像机变换
对摄像机的描述,有三个三个向量就能定义一个摄像机的位置和摄像方位:
- Position e ⃗ \vec{e} e
- gaze g ^ \hat{g} g^
- Up t ^ \hat{t} t^
M v i e w = R v i e w T v i e w M_{view} = R_{view}T_{view} Mview=RviewTview(摄像机的变换可以给分解为旋转和平移两种变换)。
- 把整个世界都移动,让摄像机的位置处于原点;再对世界旋转,把摄像机的 gaze 对到 z轴上。但是,对于把 gaze 旋转到 z 轴,Up 旋转到 y 轴。这是一件很难的事情:所以,我们考虑求摄像机的旋转矩阵的逆矩阵,因为本身它的 基向量 就是 正交向量。所以它的逆向量就是 他的转置矩阵。
T v i e w = [ 1 0 0 − x e 0 1 0 − y e 0 0 1 − z e 0 0 0 1 ] R v i e w = [ x g ^ × t ^ x t x − g − x e y g ^ × t ^ y t y − g − y e z g ^ × t ^ z t z − g − z e 0 0 0 1 ] T_{view}=\left[ \begin{matrix} 1& 0& 0& -x_e\\ 0& 1& 0& -y_e\\ 0& 0& 1& -z_e\\ 0& 0& 0& 1\\ \end{matrix} \right] \\ \\ R_{view}=\left[ \begin{matrix} x_{\hat{g}\times \hat{t}}& x_t& x_{-g}& -x_e\\ y_{\hat{g}\times \hat{t}}& y_t& y_{-g}& -y_e\\ z_{\hat{g}\times \hat{t}}& z_t& z_{-g}& -z_e\\ 0& 0& 0& 1\\ \end{matrix} \right] Tview=⎣⎡100001000010−xe−ye−ze1⎦⎤Rview=⎣⎡xg^×t^yg^×t^zg^×t^0xtytzt0x−gy−gz−g0−xe−ye−ze1⎦⎤
3、投影变换
 对于摄像机的视野,我们有两种投影方式,一个是正交投影(Orthographic Projection),另一个是透视投影(Perspective Projection)。我们使用的是后者,投影的视野形状是一个**视椎体**(Frustum),这样就能有一个近大远小的视觉效果。
对于摄像机的视野,我们有两种投影方式,一个是正交投影(Orthographic Projection),另一个是透视投影(Perspective Projection)。我们使用的是后者,投影的视野形状是一个**视椎体**(Frustum),这样就能有一个近大远小的视觉效果。 ①正交投影
要做的操作比较简单:首先平移到原点,然后将整个投影的视野缩放到一个小立方体里。
②透视投影
我们是把整个的 视椎体 挤压成半个立方体,计算的到 视椎体 中到立方体中的映射。而《GAMES101》保持近截面不变,远截面挤压成 近截面 的大小 ,让 视野 挤压成一个立方体。然后剩下的做法就和 正交投影一样的了。
其中,视椎体中任意坐标的 x,y 值都很容易用 相似三角形 来获得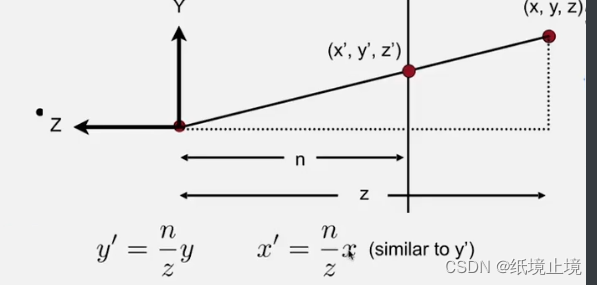
然后,我们在齐次坐标系中,四个数都同时乘以一个数,实际上整个坐标都没有改变。![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-K5j80KzD-1658471090945)(assets/image-20220525171153215.png)]](/img/e3/6332c7ea83bd8e3f544dcaae6b566f.png)
根据我们投影的向量的变化,我们能够反推出这个变换矩阵的部分的数值,留下第三行还暂时不能确定。
我们又利用这个挤压变换过程两个性质:任何在近截面点的 z 值不会变化;任何在远截面的点的 z 值不会变换。
带入近截面的点(其坐标 z值 一定是 n):
带入远截面的点(其坐标 z值 一定是 f):
这样,我们的两个方程,就能求到 M p e r s p − > o r t h o M_{persp->ortho} Mpersp−>ortho 这个变换矩阵的所有项了。之后就再做正交投影就行了。
边栏推荐
猜你喜欢
随机推荐
MySQL表的增删改查
【图形学】11 UnityShader入门(三)
PyTorch向量变换基本操作
略解损失函数
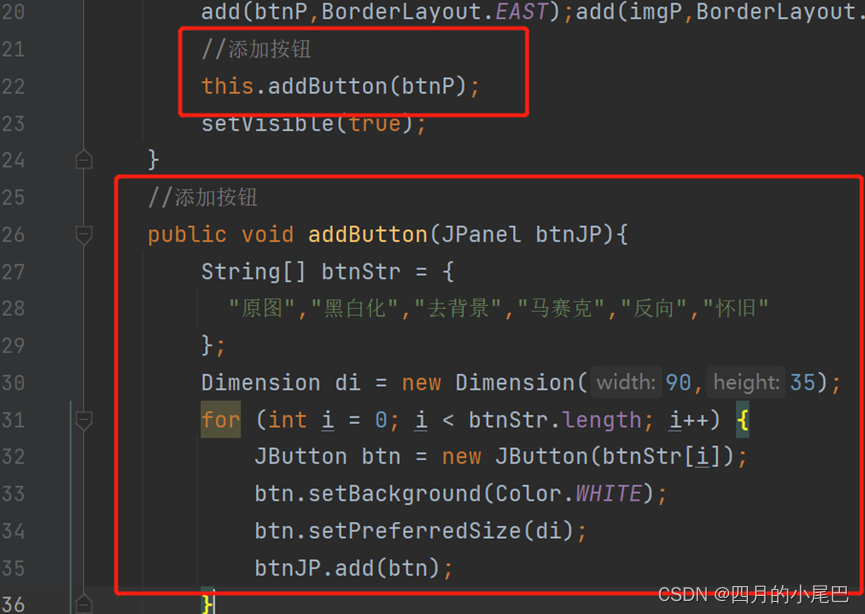
P19 美颜相机的实现——基础铺垫1
MongoDB常用命令整理
P03 线程安全 synchronized Lock
状态机控制移位寄存器multisim仿真过程中出现的状态变量和状态转移条件不匹配的问题
Electronic payment market status quo of the study: 2022 volume is expected to increase to 314.1 billion yuan
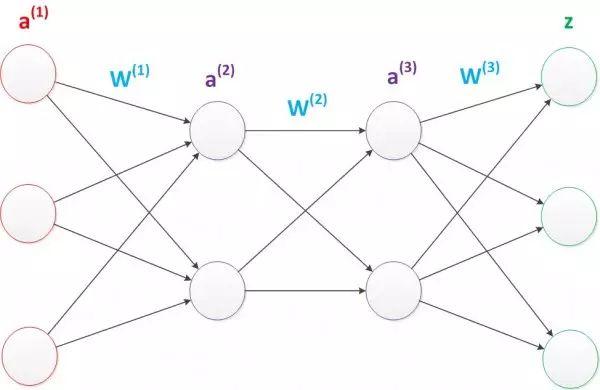
神经网络对数据的要求,神经网络分析相关性
RHCSA-配置redhat
Part 10:iOS的数据持久化(2),Sqlite,CoreData
NVIDIA CUDA 高度并行处理器编程(七):并行模式:前缀和
[Unity] GPU动画实现(二)——网格合并
在ENSP中配置DHCP服务器
Unity中获取一个物体下所有的子物体的方法
Flutter 实现一款简单的音乐播放器
C语言实现冒泡排序及对冒泡排序的优化处理
【Web】标准文档流
Food Industry Report: Research Analysis and Development Prospect Forecast of Chili Market