正则化原理的简单分析(L1/L2正则化)

在机器学习和深度学习中，为了防止模型过拟合，通常有两种办法：

第一种是人工对数据进行重要性判断，保留较重要的特征，前提是有足够的先验知识。但同时这也相当于舍弃了数据中的一部分的信息。
第二种则是正则化，采取某种约束可以自动选择重要的特征变量，自动舍弃不需要的特征变量。

常用的正则化方法有：
L1 / L2正则化:直接在原来的损失函数基础上加上一个“惩罚项”。
dropout：深度学习中最常用，即在训练的过程中随机的丢弃一些神经元。
数据增强：比如将原始图像翻转、平移、拉伸，使得模型的训练数据集增大。
提前终止法：在模型训练所得到的结果已经比较不错的时候提前终止训练。需要人工监督且具备先验知识。

L2正则化：

L2 正则化，即在原的损失函数基础上加上权重参数的平方和：

E_in 是未包含正则化项的训练样本误差，λ 是正则化参数。
为什么要加一个权重参数的平方和？可以想象，在拟合一组数据的时候，一般来说，使用高阶的多项式更容易拟合这组数据曲线。然而，这样也会使得模型变得过于复杂，容易过拟合即泛化能力差。因此可以限制高阶部分的权重，使其为0。这样便从高阶问题转移至低阶问题的求解。但是这种方法在实际中比较难以实现。因此可以限定一个较为宽松的条件：

这个限定条件的含义也很简单，即所有权重的值的和小于等于C。
那么为什么这个惩罚项（约束条件）要被设置为所有权重的和呢？下面进行一个简单的解释：

如图所示，黑色椭圆圈为E_in最小化区域，其内部有一个蓝色点为E_in最小取值的点。红色圈为限制条件的区域，且最小化的点会沿着梯度▽E_in的反方向运动，由于有限定条件，最小化的点只能在红色区域内。对于上图而言，最小化的点只能沿着红色圆切线运动。当梯度E_in的反方向与圆心指向最小化点的方向(w的方向)重合时（即平行），该损失函数被最小化。（因为梯度▽E_in在切线方向没有分量了，因此不会再沿切线移动）。

因此可得：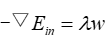

移项后即：（符号包含在λ 内）

将这个等式整体看作是梯度，得到新的损失函数：

这就是L2正则化。类似地，L1正则化是在原来的损失函数基础上加上权重参数的绝对值：

损失函数实际上包含了两个方面：一个是训练样本误差。一个是正则化项。其中，参数 λ 起到了平衡的作用。若λ 过大，约束项的C很小，即限制区域圆的区域就很小，优化后的结果离真实最小点很远，导致欠拟合。反之亦然，若λ 过小，约束项的C很大，即限制区域圆的区域就很大，优化后的结果离真实最小点很近，正则化的作用降低，导致过拟合。因此λ值的选取也十分重要。