当前位置:网站首页>4-5 Matplotlib库 散点图
4-5 Matplotlib库 散点图
2022-08-09 00:29:00 【刚入门的小仙女】
Matplotlib是一个Python的2D绘图库,通过Matplotlib,开发者可以仅需要几行代码,便可以生成折线图,直方图,条形图,饼状图,散点图等。详情可查看Matplotlib库API文档
1. 散点图
散点图也就X-Y图,它将所有的数据以点的形式展现在直角坐标系上,以显示变量之间的相互影响程度,点的位置由变量的数值决定。
通过观察散点图上的数据点的分布情况,我们可以推断出变量间的相关性。如果变量之间不存在相互关系,那么在散点图上就会表现为随机分布的离散点,如果存在某种相关性,那么大部分的数据点就会相对密集并以某种趋势呈现。数据的相关关系主要分为:正相关(两个变量值同时增长)、负相关(一个变量值增加另一个变量值下降)、不相关、线性相关、指数相关等,表现在散点图上的大致分布如下图所示。那些离点集群较远的点我们称为离群点或者异常点。
2. 绘制散点图
散点图的绘制,使用的是 plt.scatter 方法,这个方法有以下参数:
(1) x,y:分别是 x 轴和 y 轴的数据集。两者的数据长度必须一致
(2) s:点的尺寸。如果是一个具体的数字,那么散点图的所有点都是一样大小,如果是一个序列,那么这个序列的长度应该和 x 轴数据量一致,序列中的每个元素代表每个点的尺寸
(3) c:点的颜色。可以为具体的颜色,也可以为一个序列或者是一个 cmap 对象
(4) marker:标记点,默认是圆点,也可以换成其他的
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
#读取运动员数据(姓名、性别、年龄、身高、体重)且删除NaN数据
athletes = pd.read_csv('new_athlete.csv').dropna()
plt.figure(figsize=(15,5))
#男性数据
male_athletes = athletes[athletes['Sex']=='M']
#身高
male_heights = male_athletes['Height']
#体重
male_weights = male_athletes['Weight']
#平均身高
male_heights_mean = male_heights.mean()
#平均体重
male_weights_mean = male_weights.mean()
#女性数据
female_athletes = athletes[athletes['Sex']=='F']
#身高
female_heights = female_athletes['Height']
#体重
female_weights = female_athletes['Weight']
#平均身高
female_heights_mean = female_heights.mean()
#平均体重
female_weights_mean = female_weights.mean()
#绘图 s设置点的尺寸(示例:按年龄大小)
plt.scatter(male_heights,male_weights,s=male_athletes['Age'])
#alpha调节透明度
plt.scatter(female_heights,female_weights,s=female_athletes['Age'],alpha=0.5)
#绘制纵向平均线(示例:平均身高线)
plt.axvline(male_heights_mean,linewidth=1,c='r')
#绘制横向平均线(示例:平均体重线)
plt.axhline(male_weights_mean,linewidth=1,c='y')

3. 绘制回归曲线
有一组数据后,我们可以对这组数据进行回归分析,回归分析可以帮助我们了解这组数据的大体走向。回归分析按照涉及的变量的多少,分为一元回归和多元回归分析;按照自变量的多少,可分为简单回归分析和多重回归分析;按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。如果在回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且自变量之前存在线性相关,则称为多重线性回归分析。
| 自变量数量 | 是否线性 | 回归类型 |
|---|---|---|
| 1个 | 是 | 一元线性回归 |
| 多个 | 是 | 多元线性回归 |
| 1个 | 否 | 一元非线性回归 |
| 多个 | 否 | 多元非线性回归 |
from sklearn.linear_model import LinearRegression
model = LinearRegression()
#fit的第一个参数要求为二维数据 多行一列
#与 male_heights.values[:,None] 效果一致 None也可替换为np.newaxis
#male_heights.values.reshape(male_heights.shape[0],1)
#喂数据
model.fit(male_heights.values[:,np.newaxis],male_weights)
predict_male_weight = model.predict(male_heights.values[:,np.newaxis])
#绘制回归方程
plt.plot(male_heights,predict_male_weight)

边栏推荐
- 统一身份管理平台IAM单点登录流程及第三方接口设计方案
- 「复盘」面试 BAMT 回来整理 398 道高频面试题,助你拿高薪 offer
- GaN图腾柱无桥 Boost PFC(单相)二 (公式推到理解篇)
- 如何选择云服务器与轻量应用服务器?谈谈自己的看法
- 网络宽度扩充--Inception v1-v4,xception变式学习记录
- 笔记&代码 | 统计学——基于R(第四版) 第十一章 时间序列预测
- 利用Ehcache分布式缓存,轻松打造商业级高并发、高性能API接口!
- 凹凸映射Bump_Mapping
- Unity学习笔记--摄像机插值跟随
- VsCode configures your favorite fonts and backgrounds. Mom no longer worries about my boring code writing.
猜你喜欢

pycharm开启鼠标滚动调节字体大小

VsCode configures your favorite fonts and backgrounds. Mom no longer worries about my boring code writing.

整流十五—网侧低频电流谐波抑制方法及其稳定性分析

整流十—双二阶广义积分锁相
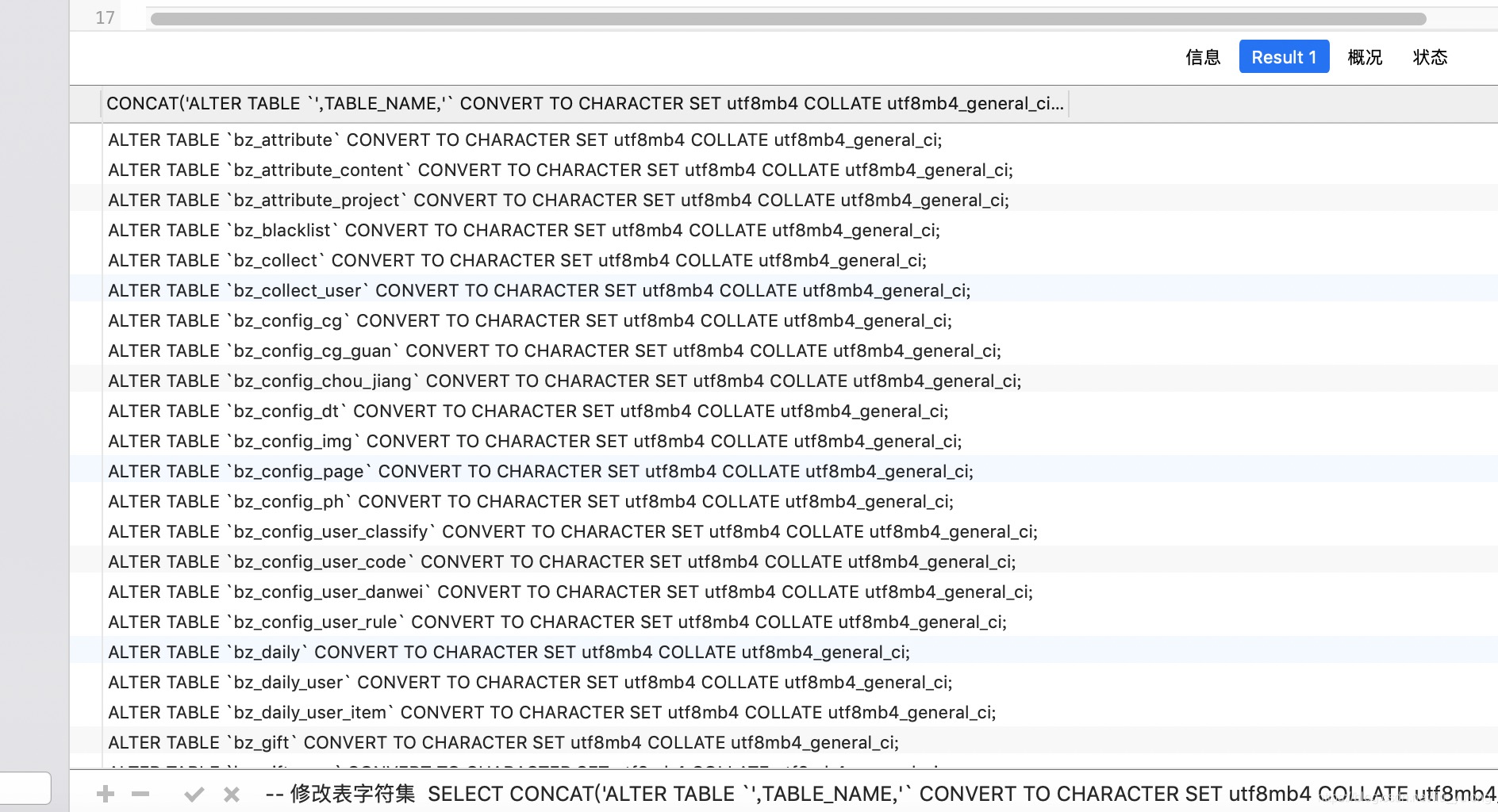
mysql 批量修改表及字段字符集

“圆梦杯”大学生智能硬件设计大赛 初赛样题——理论题作答

pycharm更改默认项目地址的方法

Sencha Touch页面跳转创建返回上一级按钮的设计思路
无代码平台邮箱入门教程

Using MySQL in Ubuntu/Linux environment: Solve the problem of com.mysql.jdbc.PacketTooBigException: Packet for query is too large
随机推荐
控件限制总结
Mysql 根据一个表数据更新另外一个表
MySQL5.7安装教程图解
mysql 批量修改表及字段字符集
小G砍树 (换根dp)
mysql在查询出来的数据前添加序号
bitset和bool哪个更快
Unity3D小白学习日记(02):U3D如何连接SQL SERVER数据库(亲测可行!)
树上启发式合并
Network In Network学习记录
轻量化网络ChannelNet--channel-wize Conv在channel维度卷积
pytorch计算模型的参数量和计算速度
LeetCode每日一题(481. Magical String)
win10出现次磁盘占用率百分之百的情况
Use jdbc to handle MySQL's utf8mb4 character set (transfer)
2021 icpc 上海 H. Life is a Game
Sencha touch中Ext.data.Store获取json串中key值的方法
torch.utils.data.DataLoader
Phoenix的安装配置以及数据处理(详细步骤)
整流九—双同步坐标系锁相原理