JS - 精度问题

今天在学习js过程中，发现了一个精度问题 2^53 -1

一探究竟

1. 根据国际标准IEEE 754，javascript浮点数的64个二进制位，从最左边开始，是这样组成的
   第1位： 符号位，0表示正数，1表示负数 (1位)
   第2位到第12位： 储存指数部分 (11位)
   第13位到第64位：储存小数部分（即有效数字 52位,除去 符号位和指数位）

符号位决定了一个数的正负，指数部分决定了数值的大小，小数部分决定了数值的精度

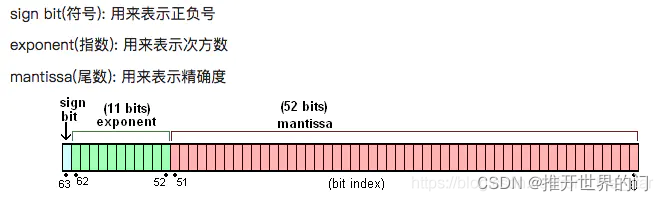
IEEE 754规定，有效数字第一位默认总是1，不保存在64位浮点数之中。
也就是说，有效数字总是1.xx...xx的形式，其中xx..xx的部分保存在64位浮点数之中，最长可能为52位

因此，javascript提供的有效数字最长为53个二进制位
精度最长为53个二进制位，意味着绝对值小于2的53次方的整数，即 ±(2^53-1)，都可以精确表示

看几个demo

0.1+0.2!=0.3
0.1表示成二进制
0.0001100110011001100110011001100110011001100110011001101
0.2表示成二进制
0.001100110011001100110011001100110011001100110011001101
在计算机里运算加起来，刚好是
0.0100110011001100110011001100110011001100110011001100111
转为十进制就是 0.30000000000000004

解释下为啥其他情况类似于0.9+0.1==1呢？
这是因为虽然加出来的二进制数也不是完全等于1，但多余下来的值1.0000000000000000000000000000000000000000000000000000001
太小了，就被舍去了

解决方法

如果对精度要求不高，直接(0.1+0.2).toFixed(2) == 0.3
利用ES6 Number新属性EPSILON Math.abs(0.1+0.2-0.3)<Number.EPSILON
利用库mathjs，math.format(math.eval(‘0.1 + 0.2’))