当前位置：网站首页>Educational Codeforces Round 81 (Rated for Div. 2)

Educational Codeforces Round 81 (Rated for Div. 2)

2022-04-23 06:21:00 【Zimba_】

A. Display The Number

题意：

在这里插入图片描述
给你 $n(2\leqslant n\leqslant 10^{5})$ 根火柴，问最大能拼成的数字。

思路：

由于其他数字的火柴都要 $4$ 个以上，除了 $1$ 需要 $2$ 根， $7$ 需要 $3$ 根，所以拼其他数字的话不如拼两个 $1$ ，而 $3$ 根火柴的时候拼 $1$ 不如拼 $7$ 。
所以当 $n$ 为偶数时，全部拼 $1$ ；
当 $n$ 为奇数时，多出来 $3$ 根拼 $7$ ，其他全部拼 $1$ 。

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1000000007;
 
int main()
{
    
    ll T;
    cin>>T;
    while(T--)
    {
    
        ll n;
        cin>>n;
        if(n%2==0)
        {
    
            for(int i=1;i<=n/2;i++)putchar('1');
            putchar('\n');
        }
        else
        {
    
            putchar('7');
            for(int i=1;i<=n/2-1;i++)putchar('1');
            putchar('\n');
        }
    }
    return 0;
}

B. Infinite Prefixes

竟然被B题卡了，有点无语，后来理思路过了。

题意：

给你一个长度为 $n(1\leqslant n\leqslant 10^{5})$ 的串 $s$ ，定义串 $t$ 是 $s$ 的无限循环。
定义一个前缀的平衡值为前缀中 $0$ 的个数减 $1$ 的个数，空串算一个前缀。
给定一个 $x(-10^{9}\leqslant x \leqslant 10^{9})$ 。
问有多少个前缀的平衡值等于 $x$ 。

思路：

我们先处理出整个串 $s$ 的平衡值 $p$ 。
定义 $s$ 串中长度为 $i$ 的前缀的平衡值为 $w_{i}$ 。
于是我们要求的就是方程 $kp+w_{i}=x$ 中， $k$ 有多少个自然数解。
先把 $p = 0$ 的情况判掉，遍历一遍如果存在 $w_{i}=x$ 则有无穷个，否则有 $0$ 个。
当 $p\neq 0$ 时，就得到了 $k=\frac{x-w_{i}}{p}$ 。
然后遍历 $i$ ，对于每一个 $w_{i}$ ，若 $x-w_{i}$ 能被 $p$ 整除，且计算出来的 $k$ 为自然数，则答案加 $1$ 。
最后 $x = 0$ 时，因为空串要考虑，所以答案再加 $1$ 。

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1000000007;
 
 
string s;
int main()
{
    
    int T;
    cin>>T;
    while(T--)
    {
    
        ll n,x;
        cin>>n>>x>>s;
        ll p=0;
        for(ll i=0;i<s.size();i++)
        {
    
            if(s[i]=='0')p++;
            else p--;
        }
        if(p==0)
        {
    
            ll ans=0,w=0;
            for(ll i=0;i<s.size();i++)
            {
    
                if(s[i]=='0')w++;
                else w--;
                if(w==x)ans++;
            }
            if(ans)cout<<-1<<endl;
            else cout<<0<<endl;
            continue;
        }
        ll ans=0,w=0;
        for(ll i=0;i<s.size();i++)
        {
    
            if(s[i]=='0')w++;
            else w--;
            if((x-w)%p==0&&(x-w)/p>=0)ans++;
        }
        if(x==0)ans++;
        cout<<ans<<endl;
    }
    return 0;
}

C. Obtain The String

题意：

给定串 $s$ 和 $t$ ，长度范围均为 $1 e 5$ 。
你有一个空串，你想要构造串 $t$ 。
每次操作时，你可以从 $s$ 中选择一个子序列，加到你的串中。
问你需要多少次操作，可以构造出串 $t$ 。
构造不出则输出 $- 1$ 。

思路：

首先，构造不出的情况可以直接判掉，即 $s$ 中不存在 $t$ 中的某个字母。
我们设一个下标表示 $s$ 中当前在找到的位置。
然后去遍历 $t$ 的每一个字母，要在 $s$ 当前找的位置后面快速找到这个字母。
然后只要预处理出 $s$ 中每一个位置上，每个字母的下一个位置，就可以快速找到那个字母了，总体复杂度 $o (26 \times n)$ 。
不太好讲清楚，具体看代码吧。

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1000000007;
 
string s,t;
int dp[100005][26];
int has[26];
int main()
{
    
    int T;
    cin>>T;
    while(T--)
    {
    
        cin>>s>>t;
        for(int i=0;i<26;i++)
        {
    
            has[i]=0;
            dp[s.size()][i]=-1;
            for(int j=s.size()-1;j>=0;j--)
            {
    
                has[s[j]-'a']=1;
                if(s[j]=='a'+i)
                {
    
                    dp[j][i]=j;
                }
                else dp[j][i]=dp[j+1][i];
            }
        }
        int times=1,cur=0,ok=1;
        for(int i=0;i<t.size();i++)
        {
    
            if(has[t[i]-'a']==0)
            {
    
                ok=0;break;
            }
            cur=dp[cur][t[i]-'a'];
            if(cur==-1)
            {
    
                times++;
                cur=dp[0][t[i]-'a']+1;
            }
            else
            {
    
                cur=dp[cur][t[i]-'a']+1;
            }
        }
        if(ok==0)cout<<-1<<endl;
        else cout<<times<<endl;
    }
    return 0;
}

D. Same GCDs

题意：

给定两个数 $a$ 和 $m$ 。 $(1\leqslant a<m\leqslant10^{10})$
问你有多少个 $x$ 满足 $0\leqslant x<m$ ，且 $g c d (a, m) = g c d (a + x, m)$ 。

思路：

之前题解有漏洞，所以换了个新的。
在这里插入图片描述
所以最后答案就是 $\frac{m}{gcd(a,m)}$ 的欧拉函数值， $\varphi(\frac{m}{gcd(a,m)})$ 。

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1000000007;
 
ll getPhi(ll n)
{
    
    ll ans=n;
    for(ll i=2;i*i<=n;i++)
    {
    
        if(n%i==0)
        {
    
            ans=ans/i*(i-1);
            while(n%i==0)n/=i;
        }
    }
    if(n>1)ans=ans/n*(n-1);
    return ans;
}
 
ll gcd(ll a,ll b)
{
    
    return b?gcd(b,a%b):a;
}
 
int main()
{
    
    ll T;
    scanf("%lld",&T);
    while(T--)
    {
    
        ll a,m;
        scanf("%lld%lld",&a,&m);
        ll w=gcd(a,m);
        ll ans=getPhi(m/w);
        printf("%lld\n",ans);
    }
    return 0;
}

E. Permutation Separation

想出来有点晚，再给点时间就过了。

题意：

给定一个 $1$ 到 $n$ 的排列 $p_{1},p_{2}…p_{n}$ ，还有移动每个位置需要的花费 $a_{i}$ 。
$(2\leqslant n\leqslant2\times 10^{5},1\leqslant a_{i}\leqslant2\times 10^{9})$
现要求你将其划分成左右两个非空集合,即 $p_{1}p_{2}…p_{k}$ 和 $p_{k+1}p_{k+2}…p_{n}$ 。
然后要选择一些左边的元素移到右边去，再选择一些右边的元素移到左边去，最后使得右边的任意元素大于左边的任意元素，其中一边为空也可。
移动元素是要花费的，就是 $a_{i}$ 。
现问你最少需要多少花费，才能满足条件。

思路：

想了挺久的。
首首先，我们的答案在最左边和最右边取个最小值。
首先，既然花钱移动了，那就没有影响了，所以不然改成删去，效果是一样的。
然后我们要确定一个方案的话，是有两个东西要去枚举的。
一个是分割的边界，即划分的集合边界。
一个是分割的数字，即左边最大数字和右边最小数字有个边界。换句话说，左边比这个大的都要删掉，右边比这个小的都要删掉。

显然暴力枚举这两个的复杂度是不够的，那么我们考虑枚举其中一个，然后快速求解另一个。
然后会发现另一个也不满足二分三分性质。
直到我在草稿本上画出了这张图。
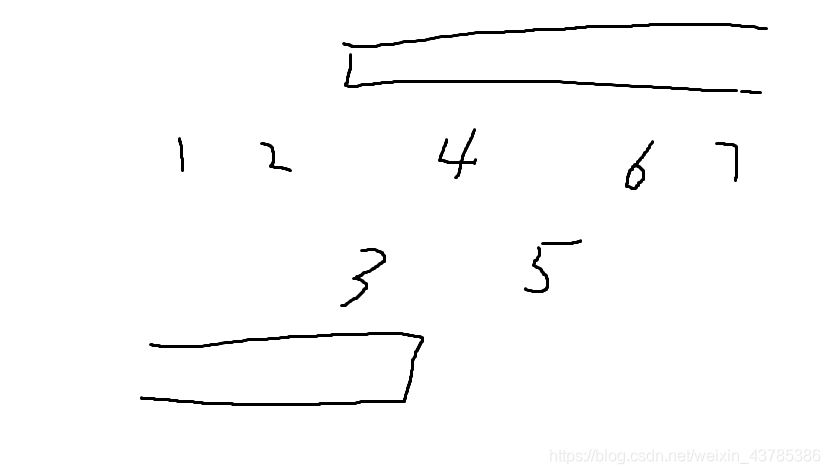
在这里插入图片描述
这张图其实给出了一个很好的计算答案的方案。
上面一排的数字表示划分在左边集合的数字。
下面一排的数字表示划分在右边集合的数字。
然后我们要枚举的是 $1$ 到 $2$ 之间的空隙， $3$ 到 $4$ 之间的空隙……计算其中最小的答案。而对于每一个空隙的计算就是，上面那排在空隙右边的数字的花费和加上下面这排在空隙左边的数字的花费和。
然后对于所有的空隙，我们要求一个最小值。
所以要用线段树来维护这些空隙，并且更新也是区间进行的。

我们再观察怎么更新。
最初时左边集合只有 $1$ 个元素，右边是 $n - 1$ 个元素。
然后我们考虑将一个元素从右边移动到了左边。
比如 $3$ 从右边集合移到了左边集合。我们发现 $3$ 在右边集合时，其左边的空隙都会加上 $a_{3}$ ，现在从右边集合拿走了，所以再给他减掉。而移到左边集合后，就给 $3$ 右边的空隙都加上 $a_{3}$ 。

至此，就是一个线段树区间更新，最值查询的模板题了。

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
 
ll tree[800005],laz[800005];
 
void push_down(ll k,ll l,ll r)
{
    
    if(l==r)
    {
    
        tree[k]=tree[k]+laz[k];
        laz[k]=0;
        return ;
    }
    laz[2*k+1]=laz[2*k+1]+laz[k];
    laz[2*k+2]=laz[2*k+2]+laz[k];
    tree[k]=tree[k]+laz[k];
    laz[k]=0;
}
 
void update(ll k,ll l,ll r,ll x,ll y,ll a)
{
    
    push_down(k,l,r);
    if(x<=l&&r<=y)
    {
    
        laz[k]=laz[k]+a;
        return ;
    }
    ll mid=(l+r)/2;
    if(x<=mid)update(2*k+1,l,mid,x,y,a);
    if(y>=mid+1)update(2*k+2,mid+1,r,x,y,a);
    push_down(2*k+1,l,mid);
    push_down(2*k+2,mid+1,r);
    tree[k]=min(tree[2*k+1],tree[2*k+2]);
}
 
ll query(ll k,ll l,ll r,ll x,ll y)
{
    
    push_down(k,l,r);
    if(x<=l&&r<=y)
    {
    
        return tree[k];
    }
    ll ans=1e18,mid=(l+r)/2;
    if(x<=mid)ans=min(ans,query(2*k+1,l,mid,x,y));
    if(y>=mid+1)ans=min(ans,query(2*k+2,mid+1,r,x,y));
    return ans;
}
ll p[200005];
ll a[200005];
int main()
{
    
    ll n;
    scanf("%lld",&n);
    for(ll i=1;i<=n;i++)scanf("%lld",&p[i]);
    for(ll i=1;i<=n;i++)scanf("%lld",&a[i]);
    ll ans=min(a[1],a[n]);
    if(p[1]!=1)update(0,1,n-1,1,p[1]-1,a[1]);
    for(ll i=2;i<=n;i++)if(p[i]!=n)update(0,1,n-1,p[i],n-1,a[i]);
    ans=min(ans,query(0,1,n-1,1,n-1));
    for(ll i=2;i<=n-1;i++)
    {
    
        if(p[i]!=n)update(0,1,n-1,p[i],n-1,-a[i]);
        if(p[i]!=1)update(0,1,n-1,1,p[i]-1,a[i]);
        ans=min(ans,query(0,1,n-1,1,n-1));
    }
    printf("%lld\n",ans);
    return 0;
}