当前位置:网站首页>保洁阿姨都能看懂的中国剩余定理和扩展中国剩余定理
保洁阿姨都能看懂的中国剩余定理和扩展中国剩余定理
2022-04-23 06:21:00 【Zimba_】
背景:
这个定理又叫孙子定理,问题的提出最早在南北朝的《孙子兵法算经》里,“有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?”,
即,一个整数除以三余二,除以五余三,除以七余二,求这个整数。
问题:
求解同余方程组,形如:(盗图,版权意识薄弱,读书人的事情那能叫偷吗?)
解决这个问题前,我们要清楚的一点。令 M = l c m ( m 1 , m 2 , … , m n ) M=lcm(m_{1},m_{2},…,m_{n}) M=lcm(m1,m2,…,mn),如果方程有解的话,答案一定是 x 0 + k M x_{0}+kM x0+kM的形式,也就是解在模M意义下唯一。
首先 x 0 x_{0} x0是方程的一组特解,其次不管代入哪个方程 k M kM kM总是会被消去。
中国剩余定理:传送门
首先提出问题的简单版本,即方程的模数两两互质。
这就是裸裸 的孙子定理了。
孙子的做法是:我们只要想办法去构造一组解就好了。
那么怎么构造?
这个构造方法和**牛顿插值法拉格朗日插值法 **类似(感谢高中数学老师)。
思考序列 1 , 2 , 3 , π 1,2,3,\pi 1,2,3,π,构造一个通项公式,使得 f ( 1 ) = 1 , f ( 2 ) = 2 , f ( 3 ) = 3 , f ( 4 ) = π f(1)=1,f(2)=2,f(3)=3,f(4)=\pi f(1)=1,f(2)=2,f(3)=3,f(4)=π。
利用拉格朗日插值法构造出函数:
f ( x ) = 1 × ( x − 2 ) ( x − 3 ) ( x − 4 ) ( 1 − 2 ) ( 1 − 3 ) ( 1 − 4 ) + f(x)=1 \times \frac{(x-2)(x-3)(x-4)}{(1-2)(1-3)(1-4)}+ f(x)=1×(1−2)(1−3)(1−4)(x−2)(x−3)(x−4)+ 2 × ( x − 1 ) ( x − 3 ) ( x − 4 ) ( 2 − 1 ) ( 2 − 3 ) ( 2 − 4 ) + 2 \times \frac{(x-1)(x-3)(x-4)}{(2-1)(2-3)(2-4)}+ 2×(2−1)(2−3)(2−4)(x−1)(x−3)(x−4)+ 3 × ( x − 1 ) ( x − 2 ) ( x − 4 ) ( 3 − 1 ) ( 3 − 2 ) ( 3 − 4 ) + 3 \times \frac{(x-1)(x-2)(x-4)}{(3-1)(3-2)(3-4)}+ 3×(3−1)(3−2)(3−4)(x−1)(x−2)(x−4)+ π × ( x − 1 ) ( x − 2 ) ( x − 3 ) ( 4 − 1 ) ( 4 − 2 ) ( 4 − 3 ) \pi \times \frac{(x-1)(x-2)(x-3)}{(4-1)(4-2)(4-3)} π×(4−1)(4−2)(4−3)(x−1)(x−2)(x−3)
这个神仙原理比较显而易见,每一项由两部分构成, × \times ×左边是每一项的数, × \times ×右边是决定项是否存在的控制因子,当 x x x为 1 1 1时,除第 1 1 1项外的其他三项控制因子为 0 0 0,而第一项的为 1 1 1,这就保证了,对应的 x x x可以得到我们想要的对应项。
然后回到我们的问题,应该如何构造一组解,满足所有的方程。
我们令 M = m 1 m 2 m 3 … m n M=m_{1}m_{2}m_{3}…m_{n} M=m1m2m3…mn。
再令 M i = M / m i M_{i}=M/m_{i} Mi=M/mi,就是我们的控制因子了。
然后我们要开始构造特解 x 0 x_{0} x0了。
按照前面的思路暴躁地 构造就好了。
我们先暴力地 把每一项都填到式子里。
x 0 = a 1 + a 2 + … + a n x_{0}=a_{1}\; \; \; \; \; \; \; \; \; \; \; \; +a_{2}\; \; \; \; \; \; \; \; \; \; \; \; +…+a_{n}\; \; \; \; \; \; \; \; \; \; \; \; x0=a1+a2+…+an
然后我们把控制因子 M i M_{i} Mi填进去。
x 0 = a 1 M 1 + a 2 M 2 + … + a n M n x_{0}=a_{1}M_{1}\; \; \; \; \; \; \; +a_{2}M_{2}\; \; \; \; \; \; \; +…+a_{n}M_{n}\; \; \; \; \; \; \; x0=a1M1+a2M2+…+anMn
此时把它带入到第 i i i个方程中,除 a i M i a_{i}M_{i} aiMi以外的其他项都会被消掉,只剩这一项。
然后我们要做的就是把 M i M_{i} Mi也消掉,只剩下 a i a_{i} ai,所以我们乘上它的逆元,就变成了最后这个式子了。
x 0 = a 1 M 1 M 1 − 1 + a 2 M 2 M 2 − 1 + … + a n M n M n − 1 x_{0}=a_{1}M_{1}M_{1}^{-1}+a_{2}M_{2}M_{2}^{-1}+…+a_{n}M_{n}M_{n}^{-1} x0=a1M1M1−1+a2M2M2−1+…+anMnMn−1
这里 M i − 1 M_{i}^{-1} Mi−1是模 m i m_{i} mi意义下的,前面都懂了的话,应该是知道的。
最后的式子要再列一遍:
x 0 ≡ a 1 M 1 M 1 − 1 + a 2 M 2 M 2 − 1 + … + a n M n M n − 1 ( m o d M ) x_{0}\equiv a_{1}M_{1}M_{1}^{-1}+a_{2}M_{2}M_{2}^{-1}+…+a_{n}M_{n}M_{n}^{-1}(mod\;M) x0≡a1M1M1−1+a2M2M2−1+…+anMnMn−1(modM)
还有,记得前提是要两两互素,不然求逆元那步会出现没有逆元的情况。
模板:(修正,改用了快速乘防止溢出)
#include <bits/stdc++.h>
using namespace std;
typedef __int128 ll;
ll fmul(ll a,ll b,ll mod)
{
ll sum=0,base=(a%mod+mod)%mod;
while(b)
{
if(b%2)sum=(sum+base)%mod;
base=(base+base)%mod;
b/=2;
}
return sum;
}
ll read()
{
int X=0,w=0; char ch=0;
while(!isdigit(ch)) {
w|=ch=='-';ch=getchar();}
while(isdigit(ch)) X=(X<<3)+(X<<1)+(ch^48),ch=getchar();
return w?-X:X;
}
void print(ll x)
{
if(x<0){
putchar('-');x=-x;}
if(x>9) print(x/10);
putchar(x%10+'0');
}
ll ex_gcd(ll a,ll b,ll& x,ll& y)
{
if(b==0)
{
x=1;y=0;
return a;
}
ll ans=ex_gcd(b,a%b,x,y);
ll tmp=x;
x=y;
y=tmp-a/b*y;
return ans;
}
ll inv(ll a,ll mod)//存在逆元条件:gcd(a,mod)=1
{
ll x,y;
ll g=ex_gcd(a,mod,x,y);
if(g!=1)return -1;
return (x%mod+mod)%mod;
}
ll a[100005],m[100005];
ll crt(ll *a,ll *m,ll n)//长度为0到n-1
{
ll M=1;
for(int i=0;i<n;i++)M=M*m[i];
ll ans=0;
for(int i=0;i<n;i++)
{
ll MM=M/m[i];
ans=(ans+fmul(fmul(a[i],MM,M),inv(MM,m[i]),M))%M;
}
return ans;
}
int main()
{
ll n;
n=read();
for(int i=0;i<n;i++)
{
m[i]=read();a[i]=read();
}
print(crt(a,m,n));
return 0;
}
扩展中国剩余定理:传送门
现在要解决问题的升级版,也就是没有模数两两互素的条件下。
既然是扩展的,那么举一反三
这是一种与前面完全不同的做法了。
考虑,当前面 i − 1 i-1 i−1个方程的通解是 c + k M c+kM c+kM( M M M是前面模数的最小公倍数)时,我们加入第 i i i个方程 x ≡ a i ( m o d m i ) x\equiv a_{i}\;(mod\;m_{i}) x≡ai(modmi)。 M M M会变成加入新的模数后的最小公倍数,我们要求在模新 M M M意义下的解。
我们把前面的通解带入新的方程,得到 c + k M ≡ a i ( m o d m i ) c+kM\equiv a_{i}\;(mod\;m_{i}) c+kM≡ai(modmi),变形为 k M ≡ a i − c ( m o d m i ) kM\equiv a_{i}-c\;(mod\;m_{i}) kM≡ai−c(modmi)。
注意此时不能对两边同乘 M M M的逆元(因为这个调了一下午的bug),因为此时不能保证 M M M有逆元。我们要求解新的 k k k,将方程转化成 M k + m i y = a i − c Mk+m_{i}y=a_{i}-c Mk+miy=ai−c。
此时如果方程无解,则方程组无解。
我们解出 k k k的值,然后加入第 i i i个方程后新的 c c c就变成了 c + k M c+kM c+kM,而M则是变成加新数的最小公倍数。
我们可以设初解为模 1 1 1意义下为 0 0 0,然后将方程组逐一加入。
模板:
#include <bits/stdc++.h>
using namespace std;
typedef __int128 ll;
inline ll read()
{
ll X=0,w=0; char ch=0;
while(!isdigit(ch)) {
w|=ch=='-';ch=getchar();}
while(isdigit(ch)) X=(X<<3)+(X<<1)+(ch^48),ch=getchar();
return w?-X:X;
}
inline void print(ll x)
{
if(x<0){
putchar('-');x=-x;}
if(x>9) print(x/10);
putchar(x%10+'0');
}
ll fmul(ll a,ll b,ll mod)
{
ll sum=0,base=(a%mod+mod)%mod;
while(b)
{
if(b%2)sum=(sum+base)%mod;
base=(base+base)%mod;
b/=2;
}
return sum;
}
ll gcd(ll a,ll b)
{
return b?gcd(b,a%b):a;
}
ll ex_gcd(ll a,ll b,ll& x,ll& y)
{
if(b==0)
{
x=1;y=0;
return a;
}
ll g=ex_gcd(b,a%b,x,y);
ll tmp=x;
x=y;
y=tmp-a/b*y;
return g;
}
ll a[100005],m[100005];
ll ex_crt(ll *a,ll *m,ll n)//长度为0到n-1
{
ll M=1,c=0;
for(int i=0;i<n;i++)
{
ll t=(a[i]%m[i]-c%m[i]+m[i])%m[i];
ll x,y;
ll g=ex_gcd(M,m[i],x,y);
if(t%g!=0)return -1;
ll tM=M;
M*=m[i]/gcd(M,m[i]);
x=fmul(t/g,(x%M+M)%M,M);
c=(c%M+fmul(x,tM,M)+M)%M;
}
return (c%M+M)%M;
}
int main()
{
ll n;
n=read();
for(int i=0;i<n;i++)
{
m[i]=read();a[i]=read();
}
print(ex_crt(a,m,n));
putchar('\n');
return 0;
}
版权声明
本文为[Zimba_]所创,转载请带上原文链接,感谢
https://blog.csdn.net/weixin_43785386/article/details/104084605
边栏推荐
- kaggle-房价预测实战
- 大型体育赛事无线通信系统
- Lead the industry trend with intelligent production! American camera intelligent video production platform unveiled at 2021 world Ultra HD Video Industry Development Conference
- Typora操作技巧说明(一).md
- Solution of self Networking Wireless Communication intercom system in Beifeng oil and gas field
- Hanlp分词器(通过spark)
- 学习笔记5-梯度爆炸和梯度消失(K折交叉验证)
- Object.create()原理,Object.create()规范,手写Object.create(),Object.create()用法
- Us photo cloud editing helps BiliBili upgrade its experience
- pytorch:关于GradReverseLayer实现的一个坑
猜你喜欢

manjaro安装与配置(vscode,微信,美化,输入法)
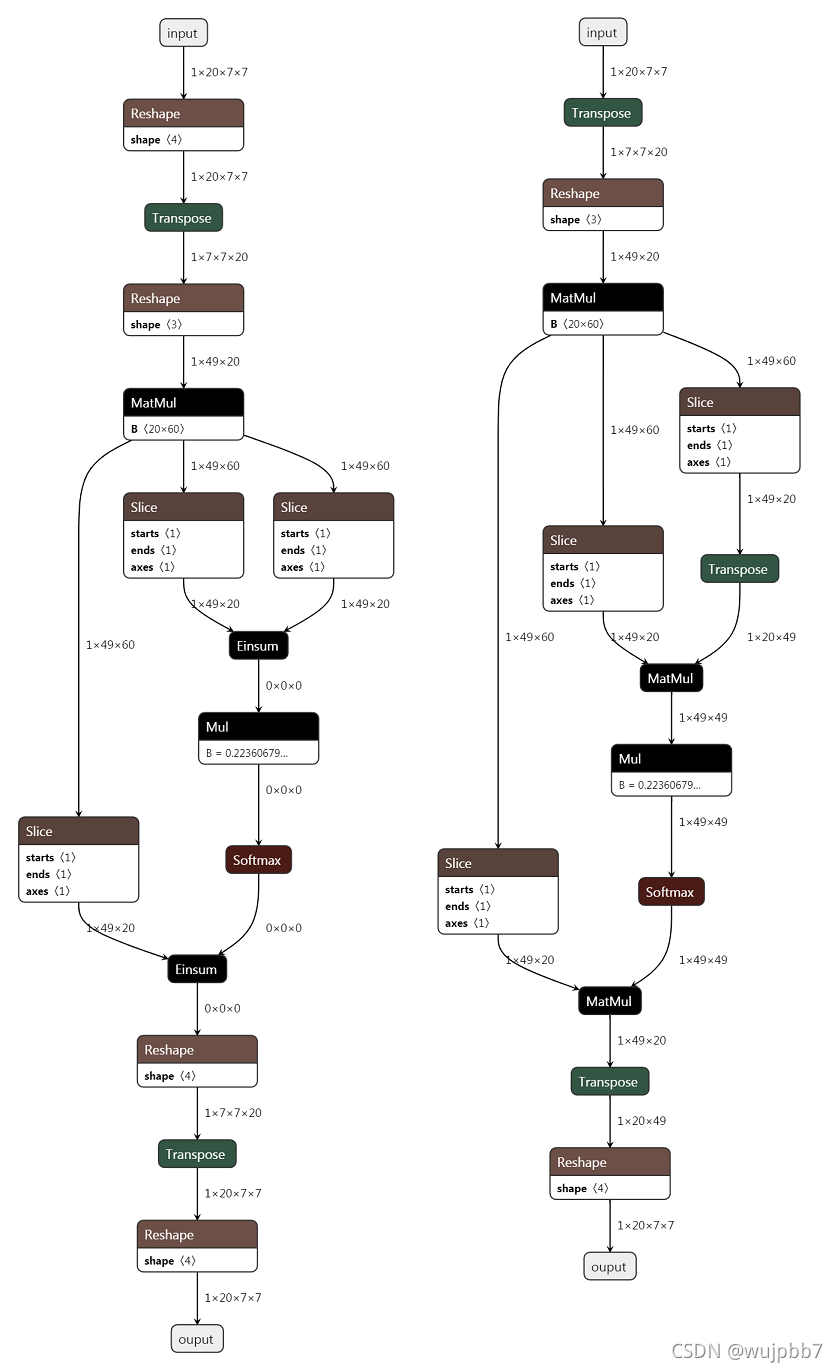
Are realrange and einsum really elegant

Take you to travel in space, and American photography technology provides comprehensive technical support for aerospace creative applet

el-table 横向滚动条固定在可视窗口底部

地铁无线对讲系统

可视化常见绘图(四)柱状图

PC端一次启动多个微信

可视化之路(十一)matplotlib颜色详解

PyTorch 10. Learning rate

枫桥学院开元名庭酒店DMR系统解决方案
随机推荐
可视化常见问题解决方案(八)共享绘图区域问题解决方案
技术小白的第一篇(表达自己)
How does the public and Private Integrated walkie talkie realize cooperative work under multi-mode communication?
商业广场无线对讲系统解决方案
可视化常见绘图(四)柱状图
LATEX公式注意事项
Meishe helps Baidu "Duka editing" to make knowledge creation easier
golang实现正则匹配:密码包含至少一位数字,字母和特殊字符,且长度8-16
P2257 YY的GCD(莫比乌斯反演)
字节数仓实习生面试sql题
PC端一次启动多个微信
Source Insight 4.0常见问题
Warning "force fallback to CPU execution for node: gather_191" in onnxruntime GPU 1.7
VScode
Solution of emergency communication system for major security incidents
海康威视面经总结
广西电网|应急空天一体化通信系统方案
安装tui-editor失败,快速解决方案
免费开源农业物联网云平台(Version:3.0.1)
kaggle-房价预测实战