当前位置:网站首页>GIS与数学
GIS与数学
2022-04-22 14:22:00 【ShirmyMao】
向量基础
1.向量的表示

2.向量运算
2.1.向量的内积(点乘)
向量的内积是一个标量,代表向量b在向量a反向上的投影


a → ⋅ b → { > 0 , 同 向 ( 锐 角 ) = 0 , 垂 直 ( 直 角 ) < 0 , 反 向 ( 钝 角 ) \overrightarrow a·\overrightarrow b \begin{cases} \gt 0, &同向(锐角)\\ =0, &垂直(直角)\\ \lt 0, &反向(钝角) \end{cases} a⋅b⎩⎪⎨⎪⎧>0,=0,<0,同向(锐角)垂直(直角)反向(钝角)
2.2.向量的外积(叉乘)
向量a和向量b的外积结果是一个向量,即垂直于a和b向量构成的平面的法向量


a → × b → = ∣ a → ∣ ⋅ ∣ b → ∣ ⋅ s i n θ { > 0 , b → 在 a → 的 逆 时 针 方 向 = 0 , 共 线 < 0 , b → 在 a → 的 顺 时 针 方 向 \overrightarrow a×\overrightarrow b =|\overrightarrow a|·|\overrightarrow b|·sinθ \begin{cases} \gt 0, &\overrightarrow b 在\overrightarrow a的逆时针方向\\ =0, &共线\\ \lt 0, &\overrightarrow b 在\overrightarrow a的顺时针方向 \end{cases} a×b=∣a∣⋅∣b∣⋅sinθ⎩⎪⎪⎨⎪⎪⎧>0,=0,<0,b在a的逆时针方向共线b在a的顺时针方向
折返线检查

思路:得到几何图形的折点,按顺时针方向进行遍历,若内角为锐角,则向量b在向量a的顺时针方向,若为钝角,则向量b在向量a的逆时针方向,可用向量的叉乘进行判断
/// <summary>
/// 获取角度限差内的节点
/// </summary>
/// <param name="geo"></param>
/// <param name="torrance">角度上限</param>
/// <returns></returns>
public static IPointCollection GetPointsWithinTorrance(IGeometry geo, double torrance)
{
bool isPolygon = false;
if (geo.GeometryType == esriGeometryType.esriGeometryPolygon)
isPolygon = true;
var points = geo as IPointCollection;
IPointCollection result = new Multipoint();
if (isPolygon)
{
///面图形得到的点为顺时针,且起点会被记录两次形成闭环
for (int i = 1; i < points.PointCount - 1; i++)
{
var point = points.Point[i];
if (isSkipPoint(points.Point[i - 1], point, points.Point[i + 1]))
continue;
var angel = CalAngel(points.Point[i - 1], point, points.Point[i + 1]);
if (angel < torrance && angel > 0)
result.AddPoint(point);
}
}
else
{
for (int i = 1; i < points.PointCount - 1; i++)
{
var point = points.Point[i];
var angel = CalAngel(points.Point[i - 1], point, points.Point[i + 1]);
if (angel < torrance && angel > 0)
result.AddPoint(point);
}
}
return result;
}
/// <summary>
/// 计算折角
/// </summary>
/// <param name="p1">起点</param>
/// <param name="p2">顶点</param>
/// <param name="p3">终点</param>
/// <returns></returns>
private static double CalAngel(IPoint p1, IPoint p2, IPoint p3)
{
var angel = Math.Atan2(p1.Y - p2.Y, p1.X - p2.X) - Math.Atan2(p3.Y - p2.Y, p3.X - p2.X);
angel = Math.Abs(angel) / Math.PI * 180;
return angel;
}
//钝角直接跳过
private static bool isSkipPoint(IPoint p1, IPoint p2, IPoint p3)
{
var va = new PointClass()
{
X = p2.X - p1.X,
Y = p2.Y - p1.Y
};
var vb = new PointClass()
{
X = p3.X - p2.X,
Y = p3.Y - p2.Y
};
///向量a×向量b=x1*y2-x2*y1,
///大于0:向量b在向量a的逆时针
///=0共线
///小于0:向量b在向量a的顺时针
///读出的多边形的点均按照顺时针排序,若叉乘大于0,则凹点,内角必然大于180
var VaCrossVb = va.X * vb.Y - vb.X * va.Y;
if (VaCrossVb > 0)
return true;
else
return false;
}
求两线交点
1.根据两点求解一般式的系数
设两个点为 (x1, y1) , (x2, y2),则有:
A = y2 - y1
B = x1 - x2
C = x2y1-x1y2
首先设交点坐标为 (x, y),两线段对应直线的一般式为:
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
那么对 1 式乘 a2,对 2 式乘 a1 得:
a2a1x + a2b1y + a2c1 = 0
a1a2x + a1b2y + a1c2 = 0
两式相减得:
y = (c1 * a2 - c2 * a1) / (a1 * b2 - a2 * b1)
同样可以推得:
x = (c2 * b1 - c1 * b2) / (a1 * b2 - a2 * b1)
其中a1b2 - a2b1 == 0时,代表两条直线重合或平行
如果(x,y)在两线段上,则(x,y)即为答案,否则交点不存在。
2.代码求解
private SGPoint GetCrossPointOfTwoLine(SGPoint p1, SGPoint p2, SGPoint p3, SGPoint p4)
{
SGPoint crossPoint = new SGPoint();
var a1 = p2.y - p1.y;
var b1 = p1.x - p2.x;
var c1 = p1.x * p2.y - p2.x * p1.y;
var a2 = p4.y - p3.y;
var b2 = p3.x - p4.x;
var c2 = p3.x * p4.y - p4.x * p3.y;
var det = a1 * b2 - a2 * b1;
//平行线
if (det == 0) return null;
crossPoint.x = (c1 * b2 - c2 * b1) / det;
crossPoint.y = (a1 * c2 - a2 * c1) / det;
return crossPoint;
}
点到几何图形的距离
/// <summary>
/// 点到几何的最短距离是否在容差内
/// </summary>
/// <param name="pGeometryA"></param>
/// <param name="pGeometryB"></param>
/// <returns></returns>
public static bool IfPointToGeometryWinthTor(IPoint point, IGeometry geo, double torrance)
{
var segments = geo as ISegmentCollection;
torrance = torrance * torrance;
for (int i = 0; i < segments.SegmentCount; i++)
{
var line = segments.Segment[i];
var dis = GetPointLineDis(line.FromPoint, line.ToPoint, point);
if (dis < torrance)
return true;
}
return false;
}
/// <summary>
/// 求点p到线段ab的最短距离的平方,避免过多开方运算
/// </summary>
/// <param name="pa"></param>
/// <param name="pb"></param>
/// <param name="p"></param>
/// <returns></returns>
private static double GetPointLineDis(IPoint a, IPoint b, IPoint p)
{
double dis = 0;
//向量AB·向量Ap
var abCrossAp = (b.X - a.X) * (p.X - a.X) + (b.Y - a.Y) * (p.Y - a.Y);
//∠PAB为钝角,最短距离为PA
if (abCrossAp <= 0)
dis = (p.X - a.X) * (p.X - a.X) + (p.Y - a.Y) * (p.Y - a.Y);
else
{
var ab2 = (b.X - a.X) * (b.X - a.X) + (b.Y - a.Y) * (b.Y - a.Y);
//p的垂线相交于AB向量的延长线上,最短距离为PB
if (abCrossAp >= ab2)
dis = (p.X - b.X) * (p.X - b.X) + (p.Y - b.Y) * (p.Y - b.Y);
//p的垂线相交于AB向量上(交点为D),最短距离为垂线的值
else
{
var r = abCrossAp / ab2;
var Dx = a.X + (b.X - a.X) * r;
var Dy = a.Y + (b.Y - a.Y) * r;
dis = (p.X - Dx) * (p.X - Dx) + (p.Y - Dy) * (p.Y - Dy);
}
}
return dis;
}
版权声明
本文为[ShirmyMao]所创,转载请带上原文链接,感谢
https://blog.csdn.net/qq_36047595/article/details/118335787
边栏推荐
- Apache iotdb's UDF Source Analysis (1)
- Openmldb pulsar connector: efficiently connect real-time data to feature Engineering
- asp.net framework配置swagger并支持上传文件
- ArcEngine符号相关
- Codeforces Round #782 (Div. 2) D. Reverse Sort Sum
- Figure keys and rooms
- CorelDRAW plug-in - CpG plug-in development - environment construction - vs2017-tlb file - CDR plug-in
- Hashtable hash table and statistics 594, 350, |554, 609, 454, 18
- jar 反编译(decode compiler) 在线工具
- 10天完成民猫电商毕设——用户模块实现(2nd day)
猜你喜欢

Methods of CRM system to improve customer experience

VDO虚拟数据优化

In depth analysis of volatile principle
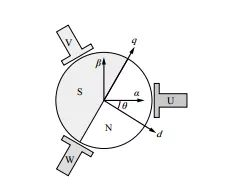
Brushless DC motor vector control (I): concept and process combing
2020 popular whole network series: This is a very suitable Android advanced - interview key and difficult data notes for collection and collection! Continuously update the high-quality interview links

With Feixiang, this task management artifact, the work is more convenient and efficient

CRM系统改善客户体验的方法

spark代码 spark-submit提交yarn-cluster模式

獲取數據庫中數值時,數據庫有值,卻為空??

Byte beating interview sharing, in order to win this offer, who knows what I have experienced
随机推荐
redis的理解
In depth analysis of blocking queue BlockingQueue (explain arrayblockingqueue and linkedblockingqueue and their applications in detail)
Lors de l'obtention d'une valeur dans la base de données, la base de données a une valeur, mais elle est vide.
Shiro之缓存管理
Understand C language -- string, escape character, comment
npm install --save 和 npm install --save-dev区别
Double pointer in the same direction, double pointer, sliding window 3, 594, |27, 26, 80, 83, 82, 611, 187, 643, 674, 209, 438, 567, 424, 76, 30
MapReduce advanced application - full sorting and secondary sorting
做好安全测试的方法
获取数组中每一项对象中的某个值的和(reduce的使用)
shell入门使用
awk命令
What happens when you run the NPM install command?
Deep transfer learning
VDO虚拟数据优化
Wonderful linkage! Principle and practice of openmldb pulsar connector
Ladder race -- l2-004 is this a binary search tree? (25 points) (recursive)
2020 popular whole network series: This is a very suitable Android advanced - interview key and difficult data notes for collection and collection! Continuously update the high-quality interview links
Kubernetes详解(六)——Pod对象部署和应用
链表 环形链表 链表判环 寻找入环节点141、142
