多目标追踪——拓展卡尔曼滤波（EKF）

Reference：
示例1：https://github.com/smartleizi/KalmanFilter-Demo/blob/master/Kalman.m
示例2：https://blog.csdn.net/weixin_46136963/article/details/110142993
示例3：https://www.mathworks.com/help/fusion/ug/extended-kalman-filters.html

不讲原理，只给实例。EKF状态转换关系如下：

示例1：匀速直线运动，观测值为位置X

clc;clear;
T = 1:1:100; %时间
trueX=(1:2:200); %真实值 

figure;%绘图
plot(T,trueX,"r",DisplayName="True Trajectory");

noise=1*randn(1,100); %均值为0，方差为1，生成100个误差项
Z=trueX+noise; %模拟的实际观测值

X=[110;110]; %随机设置的初始状态 X=[位置;速度]
P=[100 0;0 100]; %状态协方差矩阵，如果初始状态不可信，那么协方差矩阵越大越好
F=[1 1;0 1]; %状态转移矩阵
Q=[0.0001,0;0 , 0.0001]; %状态转移协方差矩阵
H=[1,0];%传感器提供的观测矩阵
R=1;%传感器的观测噪声协方差矩阵

%% 卡尔曼滤波
X_est = zeros(1,100);
for i = 1:100 %迭代次数  
  X_ = F*X;%基于上一状态预测当前状态  X_为t时刻状态预测(这里没有控制)
  P_ = F*P*F'+Q;%更新协方差  Q系统过程的协方差
  %% 计算卡尔曼增益
  K = P_*H'/(H*P_*H'+R); %这里省了计算S的过程，S=inv(H*P_*H'+R);
  %% 更新
  X = X_+K*(Z(i)-H*X_);% 得到当前状态的最优化估算值  增益乘以残差
  P = (eye(2)-K*H)*P_;%更新K状态的协方差
  X_est(i) = X(1);%保存
end
hold on;
plot(T,X_est,"g",DisplayName="Estimate Trajectory");
legend(Location="northwest");
%计算误差
figure;
plot(T, trueX-X_est,"g",DisplayName="true-est");
legend(Location="northeast");

结果：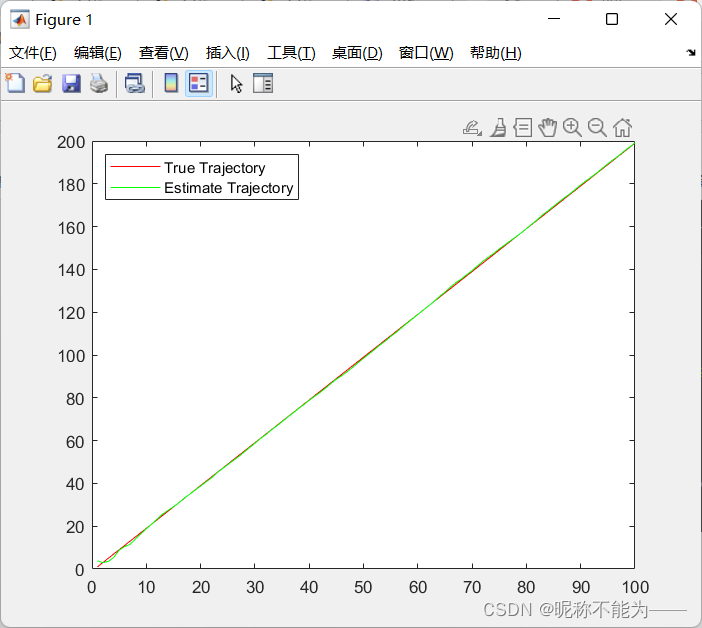

示例1变体：匀速直线运动，观测值为位置X和速度Vx

clc;clear;
T = 1:1:100; %时间
trueX=zeros(2,100); %真实值 
trueX(:,1) = [1;2];
processNoise = diag([0.01,0.01]); %真实过程噪声，该值未知，此处用模拟替代
Z=zeros(2,100); %观测值
measureNoise=diag([100,100]); %真实量测噪声，该值未知，此处用模拟替代

%%生成真实值与量测值
F=[1 1;
   0 1]; %真实的状态转移矩阵，该值未知 
for i = 2:length(Z)
    if i ~= 1
        trueX(:,i) = F*trueX(:,i-1) + sqrt(processNoise)*randn(2,1);  
    end
    Z(:,i) =  trueX(:,i)+ sqrt(measureNoise)*randn(2,1);
end

%%画图
figure;
plot(T,trueX(1,:),"r",DisplayName="True Trajectory");
xlabel("t (s)");
ylabel("x (m)");
title("Trajectory");

X=[50;1]; %初始状态 X=[位置;速度]，随机设置，可思考该参数有何影响？
P=[100 0;
   0 100]; %状态协方差矩阵，随机设置，可思考该参数有何影响？
F=[1 1;
   0 1]; %状态转移矩阵，根据运动学模型设置，可思考该参数有何影响？
Q=processNoise; %状态转移协方差矩阵，该值通过手动设定，设定的值与真实过程噪声越接近，效果越好，简单起见设置为真实过程噪声的值，有兴趣的同学可以更改这个参数试试
H=diag([1,1]); %传感器提供的观测矩阵
R=measureNoise; %传感器的观测噪声协方差矩阵，该值通过手动设定，设定的值与真实过程噪声越接近，效果越好，简单起见设置为真实过程噪声的值，有兴趣的同学可以更改这个参数试试

%% 卡尔曼滤波
X_est = zeros(1,100);
for i = 1:100 %迭代次数  
  X_ = F*X; %基于上一状态预测当前状态  X_为t时刻状态预测(这里没有控制)
  P_ = F*P*F'+Q; %更新协方差  Q系统过程的协方差
  %% 计算卡尔曼增益
  K = P_*H'/(H*P_*H'+R);
  %% 更新
  X = X_+K*(Z(:,i)-H*X_); %得到当前状态的最优化估算值  增益乘以残差
  P = (eye(2)-K*H)*P_; %更新K状态的协方差
  X_est(i) = X(1); 
end
hold on;
plot(T,X_est,"g",DisplayName="Estimate Trajectory");
legend(Location="northwest");
%计算误差
figure;
plot(T, trueX(1,:)-X_est,"g",DisplayName="real-est");
legend(Location="northeast");

结果：

示例2：非线性运动，大家可以参考链接。

示例3：matlab官方EKF例子，二维平面下物体匀速直线运动，观测值为角度angle和距离range

clc;clear;
tic;
rng(2022);    % For repeatable results
dt = 0.2;     % seconds
simTime = 20; % seconds
tspan = 0:dt:simTime;
trueInitialState = [30; 1; 40; 1]; % [x;vx;y;vy]
initialCovariance = diag([100,1e3,100,1e3]);
processNoise = diag([0; .01; 0; .01]); % Process noise matrix
measureNoise = diag([2e-6;1]); % Measurement noise matrix. Units are m^2 and rad^2.
numSteps = length(tspan);
trueStates = NaN(4,numSteps);
trueStates(:,1) = trueInitialState;
estimateStates = NaN(size(trueStates));
measurements = NaN(2,numSteps);
for i = 2:length(tspan)
    if i ~= 1
        trueStates(:,i) = stateModel(trueStates(:,i-1),dt) + sqrt(processNoise)*randn(4,1);  
    end
    measurements(:,i) = measureModel(trueStates(:,i)) + sqrt(measureNoise)*randn(2,1);
end
figure(1)
plot(trueStates(1,1),trueStates(3,1),"r*",DisplayName="Initial Truth")
hold on
plot(trueStates(1,:),trueStates(3,:),"r",DisplayName="True Trajectory")
xlabel("x (m)")
ylabel("y (m)")
title("True Trajectory")
axis square
figure(2)
subplot(2,1,1)
plot(tspan,measurements(1,:)*180/pi)
xlabel("time (s)")
ylabel("angle (deg)")
title("Angle and Range")
subplot(2,1,2)
plot(tspan,measurements(2,:))
xlabel("time (s)")
ylabel("range (m)")
filter = trackingEKF(State=[35; 0; 45; 0],StateCovariance=initialCovariance, ...
    StateTransitionFcn=@stateModel,ProcessNoise=processNoise, ...
    MeasurementFcn=@measureModel,MeasurementNoise=measureNoise);
estimateStates(:,1) = filter.State;
for i=2:length(tspan)
    predict(filter,dt);
    estimateStates(:,i) = correct(filter,measurements(:,i));
end
figure(1)
plot(estimateStates(1,1),estimateStates(3,1),"g*",DisplayName="Initial Estimate")
plot(estimateStates(1,:),estimateStates(3,:),"g",DisplayName="Estimated Trajectory")
legend(Location="northwest")
title("True Trajectory vs Estimated Trajectory")
toc;
disp(["运行时间：", num2str(toc)]);
function stateNext = stateModel(state,dt)
    F = [1 dt 0  0; 
         0  1 0  0;
         0  0 1 dt;
         0  0 0  1];
    stateNext = F*state;
end

function z = measureModel(state)
    angle = atan(state(3)/state(1));
    range = norm([state(1) state(3)]);
    z = [angle;range];
end

结果：

在这个官方示例中，调用了集成好的 trackingEKF对象，这样虽然调用起来比较方便，但不利于原理的理解，现在考虑如何自己重写一下该示例。因为该运动为匀速直线运动，求一下状态转移矩阵的一阶雅可比矩阵，结果为F。现在只需要求观测矩阵的一阶雅可比矩阵即可。首先，有如下公式
angle = arctan(Y/X);
range = sqrt(XX+YY);
所以，观测矩阵的一阶雅可比矩阵为：
H = [∂angle/∂X, ∂angle/∂Vx, ∂angle/∂yY ∂angle/∂Vy;  =  [∂angle/∂X, 0, ∂angle/∂Y, 0;
    ∂range/∂X, ∂range/∂Vx, ∂range/∂Y, ∂range/∂Vy];   ∂range/∂x, 0, ∂range/∂y, 0];
对应的传感器观测噪声协方差矩阵：
R = [2e-6, 0;
   0,  1];
求出这两项以后，按照示例1的逻辑来写就行了。代码如下：

clc;clear;
tic;
rng(2022);    % For repeatable results
dt = 0.2;     % seconds
simTime = 20; % seconds
tspan = 0:dt:simTime;
trueInitialState = [30; 1; 40; 1]; % [x;vx;y;vy]
initialCovariance = diag([100,1e3,100,1e3]);
processNoise = diag([0; 1e-2; 0; 1e-2]); % Process noise matrix
measureNoise = diag([2e-6;1]); % Measurement noise matrix. Units are m^2 and rad^2.
numSteps = length(tspan);
trueStates = NaN(4,numSteps);
trueStates(:,1) = trueInitialState;
estimateStates = NaN(size(trueStates));
measurements = NaN(2,numSteps);
for i = 2:length(tspan)
    if i ~= 1
        trueStates(:,i) = stateModel(trueStates(:,i-1),dt) + sqrt(processNoise)*randn(4,1);  
    end
    measurements(:,i) = measureModel(trueStates(:,i)) + sqrt(measureNoise)*randn(2,1);
end

figure(1)
plot(trueStates(1,1),trueStates(3,1),"r*",DisplayName="Initial Truth")
hold on
plot(trueStates(1,:),trueStates(3,:),"r",DisplayName="True Trajectory")
xlabel("x (m)")
ylabel("y (m)")
title("True Trajectory")
axis square

%%filter
X = [35; 0; 45; 0];
P = initialCovariance;
F = [1 dt 0  0; 
     0  1 0  0;
     0  0 1 dt;
     0  0 0  1];
Q = processNoise;
syms x y vx vy; 
jacobianH = jacobian([atan((y)/(x));norm([x y])], [x, vx, y, vy]);
R = measureNoise;

estimateStates(:,1) = X;
for i=2:length(tspan)
    X_ = F*X;%基于上一状态预测当前状态  X_为t时刻状态预测(这里没有控制)
    P_ = F*P*F'+Q;%更新协方差  Q系统过程的协方差
    %% 计算卡尔曼增益
    H = double(subs(jacobianH,{
    x,vx,y,vy},{
    X_(1),X_(2),X_(3),X_(4)}));
    K = P_*H'/(H*P_*H'+R);
    %% 更新
    X = X_+K*(measurements(:,i)-measureModel(X_));% 得到当前状态的最优化估算值  增益乘以残差
    P = (eye(4)-K*H)*P_;%更新K状态的协方差
    estimateStates(:,i) = X;
end

figure(1)
plot(estimateStates(1,1),estimateStates(3,1),"g*",DisplayName="Initial Estimate")
plot(estimateStates(1,:),estimateStates(3,:),"g",DisplayName="Estimated Trajectory")
legend(Location="northwest")
title("True Trajectory vs Estimated Trajectory")
toc;
disp(["运行时间：", num2str(toc)]);
function stateNext = stateModel(state,dt)
    F = [1 dt 0  0; 
         0  1 0  0;
         0  0 1 dt;
         0  0 0  1];
    stateNext = F*state;
end

function z = measureModel(state)
    angle = atan(state(3)/state(1));
    range = norm([state(1) state(3)]);
    z = [angle;range];
end

结果：