Review the logarithmic probability

• In my last article ：https://blog.csdn.net/qq_42902997/article/details/124255802?spm=1001.2014.3001.5501 The principle of logistic regression and optimization objectives are described in ：
  • Performed at each gradient descent step in , We all need to calculate each sample , For samples $x_i$, Its label is $y_i$, The vector of the parameter he needs to calculate can be expressed as ${\theta }^T$（ That includes $b$）
  • We can argue that ${\theta }^T\cdot x_i$ after sigmoid The result of function processing is $\widehat{y_i}$ namely ,$\widehat{y_i}=\sigma ({\theta }^T\cdot x_i)$
  • In this case , Our loss for each sample can be expressed as ：$L(y_i,\widehat{y_i})$ Again because $y_i$ There are two different situations for the value of , We use a formula to express the optimization objectives in these two different cases $L(y_i,\widehat{y_i})=-{\widehat{y_i}}^{y_i}(1-\widehat{y_i}{)}^{1-y_i}$, after $log$ After transformation, the final loss function for a sample is obtained ：$$L(y_i,\widehat{y_i})=-y_{i}log(\widehat{y_i})+(1-y_i)log(1-\widehat{y_i})(1)$$
  • thus , Extend to the entire dataset $m$ The total cost function of a sample can be written as ：$$-\frac{1}{m}{\Sigma }_{i=1}^m{y}_{i}log(\widehat{y_i})+(1-y_i)log(1-\widehat{y_i})+\frac{\lambda }{2m}{\Sigma }_{j=1}^n{\theta }_j^2(2)$$

  The second part of the formula is the regularization part

• The core of logarithmic probability is the introduction of sigmoid Nonlinear functions , Thus, the task of linear regression can evolve into a classification task ,sigmoid Function as follows ：
  
  • The symbols here ${\theta }^{T}x$ It means the same as the above , there $z={\theta }^{T}x$ In fact, it is equivalent to $\widehat{y_i}$
  • When this $x$ The corresponding real label is $y=1$ When （ Positive samples ）, We hope $h_{\theta }(x)$ The value of is best approximated infinitely $1$, In other words , We want to be sigmoid Before mapping ${\theta }^{T}x$ The bigger the better , namely ${\theta }^{T}x>>0$
  • And when $y=0$ When （ Negative sample ）, And we hope $h_{\theta }(x)$ The value of is best approximated infinitely $0$, namely ${\theta }^{T}x<<0$

Another perspective of logistic regression cost function

• Look at the formula （1） The cost function given ：

$$L(y_i,\widehat{y_i})=-y_{i}log(\widehat{y_i})+(1-y_i)log(1-\widehat{y_i})$$

• If you write the formula more completely , Into the $h_{\theta }(x)$ The definition of , And remove the subscript $i$ （ Because we don't study all the samples in the whole data set for the time being , We only study the case of one sample , Not for the time being $i$ To distinguish samples ） We can get the following formula ：

$$\begin{gathered} L(y,\hat{y})=-ylog(\frac{1}{1+e^{-{\theta }^{T}x}})+(1-y)log(1-\frac{1}{1+e^{-{\theta }^{T}x}}) \\ =y(-log(\frac{1}{1+e^{-{\theta }^{T}x}}))+(1-y)log(1-\frac{1}{1+e^{-{\theta }^{T}x}})(3) \end{gathered}$$

In this formula （3） Let's take a look at it alone $y=1$ and $y=0$ The case when , Look at the goals they want to optimize ：

• When $y=1$ When (${\theta }^{T}x>>0)$ By analyzing the formula (3) Only the first half is left $$-log(\frac{1}{1+e^{-{\theta }^{T}x}})$$, This will be ${\theta }^{T}x=z$ We can get a follow $z$ Curve of value change ：
  
  • When $z$ When the value of gradually increases , The value of this function tends to $0$ Of
  • That explains , Why to be $y=1$ Usually when ${\theta }^{T}x$ Set it very big . This is because in the $y=1$ The whole loss function $L(y,\hat{y})$ There's only... Left $-log(\frac{1}{1+e^z})$ At this time, set a big ${\theta }^{T}x$ It's going to lead to the whole thing $L(y,\hat{y})$ Very small , It will reduce as much as possible loss Purpose .
• Empathy , about $y=0$ The situation of , You can also see a curve when you come $L(y,\hat{y})$:
  
  • You can also draw an intuitive conclusion from this diagram , When $y=0$ When , take ${\theta }^{T}x$ The setting is small , Because this time will also lead to $L(y,\hat{y})$ Very small

SVM Improvement

• SVM It can be seen as improving the loss function on the basis of logarithmic probability regression ,logistic regression The loss function can be divided into two parts , It has also been discussed above , Look at here SVM The design of the , He put the two parts in $1$ and $-1$ Pull the value between to $0$ 了 , It's hard $y=1$ and $y=0$ A gap has been dug between the situation of .
  

• In this case, how to express in mathematical form SVM What about the loss function of ？

• Let's put the original formula (3) The loss in is divided into two parts , The front part is written as $$cos{t}_1(z)generationOn\; behalf\; of-log(\frac{1}{1+e^{-z}})(4)$$

• The latter part is written as ：
  $$cos{t}_0(z)generationOn\; behalf\; of-log(1-\frac{1}{1+e^{-z}})(5)$$

• $cost$ The subscripts of indicate $y=1$ ($cos{t}_1$) perhaps $y=0$ ($cos{t}_0$) The situation of , So for a sample $x$,SVM The loss can be caused by logistic regression The loss evolved from , As follows ：
  $$L(y,\hat{y})=ycos{t}_1({\theta }^{T}x)+(1-y)cos{t}_0({\theta }^{T}x)(6)$$

• Further, we can get SVM The cost of the whole sample set under representation can be expressed as ：
  $$\frac{1}{m}{\Sigma }_{i=1}^m{y}_{i}cos{t}_1({\theta }^T{x}_i)+(1-y_i)cos{t}_0({\theta }^T{x}_i)+\frac{\lambda }{2m}{\Sigma }_{j=1}^n{\theta }_j^2(7)$$

• For this equation , We use a $C$ Parameter to control the proportion of the first item , So as to remove the $\lambda$ and $m$

• $$C{\Sigma }_{i=1}^m{y}_{i}cos{t}_1({\theta }^T{x}_i)+(1-y_i)cos{t}_0({\theta }^T{x}_i)+\frac{1}{2}{\Sigma }_{j=1}^n{\theta }_j^2(8)$$

• $SVM$ There's another feature , That is, a probability value will not be output in the end , But more simply $0$ perhaps $1$

Why? SVM It's called maximum interval classifier

• stay SVM Because we have adopted more stringent measures , That is, not just hope ${\theta }^{T}x>=0$ They are classified as positive samples , We want the criteria to be strict to ${\theta }^{T}x>=1$; alike , For negative samples , We also hope that the criterion of discrimination can be strict to ${\theta }^{T}x<=-1$ Not just less than $0$

• So we distinguish this from logistic regression As SVM Constraints of ：

  ${\theta }^{T}x>=1,if{y}_i=1$
  ${\theta }^{T}x<=-1,if{y}_i=0$

• Through the formula （8） We can know , When we do SVM In the optimization process, a particularly large $C$ Then our optimization process will expect the value of the first term ${\Sigma }_{i=1}^m{y}_{i}cos{t}_1({\theta }^T{x}_i)+(1-y_i)cos{t}_0({\theta }^T{x}_i)$ As small as possible , The closer the $0$ The better , Because that's the only way , Whole loss The value of is not very big , In order to meet the optimization goal .

• In this case, we assume that we have achieved our goal , bring $C$ The latter item is small enough , Suppose you reach $0$, So the whole loss function can be abbreviated as ：
  $$C\cdot 0+\frac{1}{2}{\Sigma }_{j=1}^n{\theta }_j^2(9)$$

• Therefore, the optimization goal becomes to minimize $\frac{1}{2}{\Sigma }_{j=1}^n{\theta }_j^2$; And this part is the guarantee of the maximum interval Let's analyze it in detail .

Vector dot product

• For two vectors $\vec{u}=[u_1,u_2{]}^T,\vec{v}=[v_1,v_2{]}^T$
• The dot product of these two vectors can be regarded as $\vec{v}$ In vector $\vec{u}$ The projection on the , The length of the projection is $p$,$\vec{u}$ The length of can be expressed as $||u||$ So the dot product of two vectors can be expressed as ： $$\vec{u}\cdot \vec{v}=p\cdot ||u||=u_1{v}_1+u_2{v}_2$$

According to the preliminary knowledge of dot product , To achieve $$mi{n}_{\theta }\frac{1}{2}{\Sigma }_{j=1}^n{\theta }_j^2$$ amount to $$mi{n}_{\theta }\frac{1}{2}{\Sigma }_{j=1}^n||{\theta }_j|{|}^2$$ And the original constraints ：

${\theta }^{T}x>=1,if{y}_i=1$
${\theta }^{T}x<=-1,if{y}_i=0$
You can write ：
$p_i\cdot ||\theta ||>=1,if{y}_i=1$
$p_i\cdot ||\theta ||<=-1,if{y}_i=0$

Why? SVM Don't choose small margin

• Suppose there is a pile of points that need to be separated （ Red and blue ）
• Suppose there is an optional decision boundary （ Green line ）, its margin A very small , Now let's see why SVM Will not choose the decision in this case .

Add a little knowledge ,${\theta }^T$ This vector is perpendicular to the decision boundary . For example, if I have a hyperplane $y=-x$ As a decision boundary （ Here, for simplicity, the intercept is temporarily used as $0$ （${\theta }_0=0$） What if ）,$y=-x$ You can also write ： $x+y=0$ So his ${\theta }^T$ The vector is expressed as ${\theta }^T=[1,1]$;
So to sum up , The decision boundary is a slope of $-1$ The straight line of , And the corresponding ${\theta }^T$ The vector does point diagonally to the top right , As shown in the figure below ：

• Continue to look at the current situation , According to our existing knowledge of the dot product above , We can get that the loss of the two points closest to the decision boundary can be expressed as ：
  • $p_1\cdot ||\theta ||$
  • $p_2\cdot ||\theta ||$
    
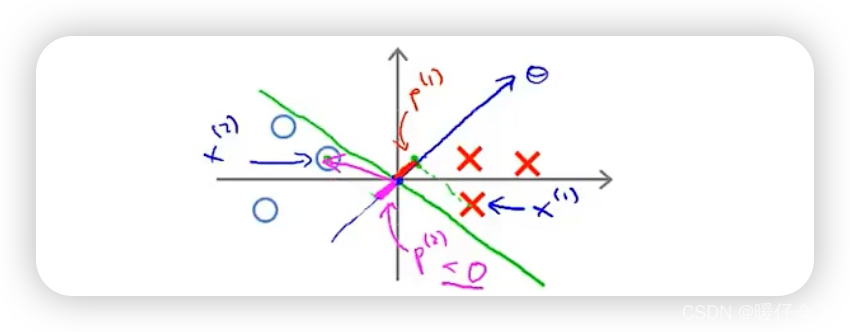
• And because of this margin A very small , Means $p_1$ and $p_2$ A very small , Don't forget our constraints above ：

  $p_i\cdot ||\theta ||>=1,if{y}_i=1$
  $p_i\cdot ||\theta ||<=-1,if{y}_i=0$

• So if $p_1$ and $p_2$ A very small , We have to make sure that $||\theta ||$ Great to meet the results $>=1$ perhaps $<=-1$ The requirements of
• and $||\theta ||$ It means violating the optimization goal $$mi{n}_{\theta }\frac{1}{2}{\Sigma }_{j=1}^n{\theta }_j^2$$
• Therefore, in order not to make the optimization objectives and constraints conflict , We have to ensure that the decision boundary margin The larger . So let's take a look at the right situation , And make corresponding analysis .

When SVM Choose a reasonable margin

• In this situation , hypothesis margin The straight line can be used $x=0$ To express ; That is, it can be expressed as $x+0y=0$ So the corresponding vector ${\theta }^T=[1,0]$

• At this time, the losses of the two positive and negative samples closest to the decision boundary are ：
  

  • $p_1\cdot ||\theta ||$
  • $p_2\cdot ||\theta ||$
  • And because the $p_1$, $p_1$ Relatively large , therefore ${\theta }^T$ Can guarantee that $||\theta ||$ The constraints are met in the case of ：

  $p_i\cdot ||\theta ||>=1,if{y}_i=1$
  $p_i\cdot ||\theta ||<=-1,if{y}_i=0$

• So compare two different SVM Decision boundaries , Because the second can be in $||\theta ||$ In small cases, the constraints are guaranteed to be established , therefore SVM Will choose the big one margin Classification strategy .