Likou 221 questions, the largest square

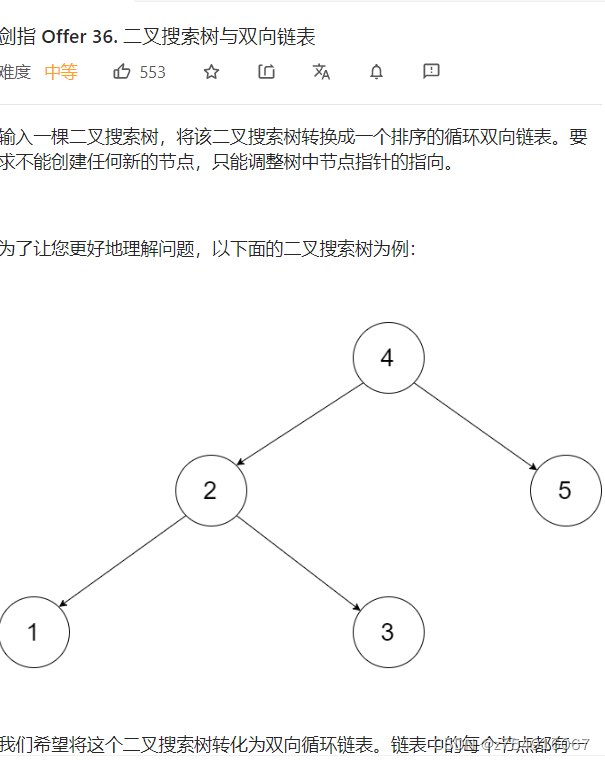
力扣221题,最大正方形

题目描述

在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积.

输入输出样例

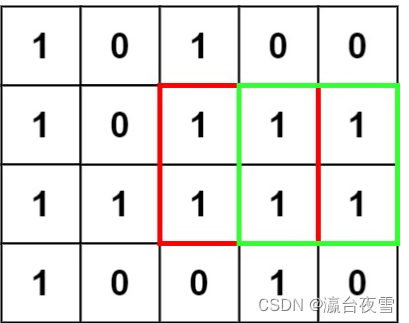
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

输入：matrix = [["0","1"],["1","0"]]
输出：1

输入：matrix = [["0"]]
输出：0

解法一：暴力解法

//使用暴力解法
//Iterates over each element in the matrix each time it is encountered1,That element is the upper left corner of the square
//Determine the upper left corner of the square,根据左上角所在的行和列计算可能的最大正方形的边长
//判断右下,右,Whether the following is an element1

//时间复杂度为O(mn*min(m,n)^2)
//空间复杂度 为 O(1)
    int maximalSquare(vector<vector<char>>&matrix)
    {
    
        int rowLength=matrix.size();
        int colLength=matrix[0].size();

        if(rowLength==0||colLength==0)
        {
    
            return 0;
        }

        //The maximum side length for storing the current value
        int maxSide=0;

        //Iterate over every space in the space1的结点
        for(int i=0;i<rowLength;i++)
        {
    
            for(int j=0;j<colLength;j++)
            {
    
                if(matrix[i][j]=='1')
                {
    
                    maxSide=max(maxSide,1);

                    //Calculates the current maximum possible edge length
                    int currMaxSide=min(rowLength-i,colLength-j);

                    //Check whether the value in the lower right exists
                    for(int k=1;k<currMaxSide;k++)
                    {
    
                        //设置标志位,Indicates the current lower right,右侧,Whether the lower side is both1
                        bool flag=true;
                        if(matrix[i+k][j+k]=='0')
                        {
    
                            break;
                        }

                        //Bottom left verification is successful,then verify that the right and lower sides are1
                        for(int m=0;m<k;m++)
                        {
    
                            if(matrix[i+k][j+m]=='0'||matrix[i+m][j+k]=='0')
                            {
    
                                flag=false;
                                break;
                            }
                        }

                        if(flag)
                        {
    
                            maxSide=max(maxSide,k+1);
                        }

                        else
                        {
    
                            break;
                        }
                    }
                }
            }
        }
        int maxSquare=maxSide*maxSide;
        return maxSquare;


    }

解法二：使用动态规划

//使用动态规划的方法
    //动态规划,Take the lower right corner as the initial value condition,且只包含1的正方形的边长的最大值
    //状态转移方程 dp[i]由上方,左方,左上方的dp值决定
    //dp[i][j]=min(dp[i-1][j],dp[i-1][j-1],dp[i][j-1])+1
    //时复：O(mn)
    //空复：O(mn)
    int maximalSquare2(vector<vector<char>>&matrix)
    {
    
        int rowLength=matrix.size();
        int colLength=matrix[0].size();

        if(rowLength==0||colLength==0)
        {
    
            return 0;
        }

        //建立动态规划数组
        vector<vector<int>>dp(rowLength,vector<int>(colLength,0));

        //Initialize dynamic programming arrays and transition equations
        int maxSides=0;
        for(int row=0;row<rowLength;row++)
        {
    
            for(int col=0;col<colLength;col++)
            {
    
                if(matrix[row][col]=='1')
                {
    
                    //对row和coldifferent locations for classification discussions
                    //因为在第一行,The first line is whateverdp的值肯定为1
                    if(row==0||col==0)
                    {
    
                        dp[row][col]=1;
                    }
                    else{
    
                        //转移方程
                        dp[row][col]=min(dp[row-1][col-1],min(dp[row-1][col],dp[row][col-1]))+1;
                    }
                    maxSides=max(maxSides,dp[row][col]);

                }
            }
        }
        return maxSides*maxSides;
    }