当前位置:网站首页>【The sword refers to Offer II 091. Paint the house】
【The sword refers to Offer II 091. Paint the house】
2022-08-09 16:47:00 【wangyunpeng33】
剑指 Offer II 091. 粉刷房子
假如有一排房子,共 n 个,每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种,你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同.
当然,因为市场上不同颜色油漆的价格不同,所以房子粉刷成不同颜色的花费成本也是不同的.每个房子粉刷成不同颜色的花费是以一个 n x 3 的正整数矩阵 costs 来表示的.
例如,costs[0][0] 表示第 0 号房子粉刷成红色的成本花费;costs[1][2] 表示第 1 号房子粉刷成绿色的花费,以此类推.
请计算出粉刷完所有房子最少的花费成本.
示例 1:
输入: costs = [[17,2,17],[16,16,5],[14,3,19]]
输出: 10
解释: 将 0 号房子粉刷成蓝色,1 号房子粉刷成绿色,2 号房子粉刷成蓝色.
最少花费: 2 + 5 + 3 = 10.
示例 2:
输入: costs = [[7,6,2]]
输出: 2
题解
动态规划
Each house can be painted in one of three colors,It is necessary to calculate the minimum cost of painting all the houses under the condition that the colors of the adjacent houses are different.As when known before painting ii the minimum cost of a house,According to Stucco pp i + 1 i+1 i+1 No. The cost of the house can be calculated before painting i + 1 i+1 i+1The minimum cost of a house,So the minimum cost can be calculated using dynamic programming.
Since each house can be painted in one of three colors,Therefore, the minimum cost of painting in three colors needs to be considered separately.
用 dp [ i ] [ j ] \textit{dp}[i][j] dp[i][j] 表示粉刷第 0 号房子到第 i 号房子且第 i 号房子被粉刷成第 j 种颜色时的最小花费成本.由于一共有 n a house and 3 种颜色,因此 0 ≤ i < n 0≤i<n 0≤i<n, 0 ≤ j < 3 0≤j<3 0≤j<3.
when only the first 0 When the house was painted,对于每一种颜色,The total cost will be the first 0 The cost of painting a house in that color,So the boundary conditions are :对于任意 0 ≤ j < 3 , dp [ 0 ] [ j ] = costs [ 0 ] [ j ] 0≤j<3,\textit{dp}[0][j] = \textit{costs}[0][j] 0≤j<3,dp[0][j]=costs[0][j].
对于 1 ≤ i < n 1≤i<n 1≤i<n,第 i No. House and No i−1 No. House color must be different,因此当第 i When the house is painted in a certain color,第 i−1 House No. can only be painted in one of the other two colors.当第 i House No. was painted in three colors,粉刷第 0 号房子到第 i The minimum cost of house No. is calculated as follows:
dp [ i ] [ 0 ] = min ( dp [ i − 1 ] [ 1 ] , dp [ i − 1 ] [ 2 ] ) + costs [ i ] [ 0 ] dp [ i ] [ 1 ] = min ( dp [ i − 1 ] [ 0 ] , dp [ i − 1 ] [ 2 ] ) + costs [ i ] [ 1 ] dp [ i ] [ 2 ] = min ( dp [ i − 1 ] [ 0 ] , dp [ i − 1 ] [ 1 ] ) + costs [ i ] [ 2 ] \begin{aligned} \textit{dp}[i][0] &= \min(\textit{dp}[i - 1][1], \textit{dp}[i - 1][2]) + \textit{costs}[i][0] \\ \textit{dp}[i][1] &= \min(\textit{dp}[i - 1][0], \textit{dp}[i - 1][2]) + \textit{costs}[i][1] \\ \textit{dp}[i][2] &= \min(\textit{dp}[i - 1][0], \textit{dp}[i - 1][1]) + \textit{costs}[i][2] \end{aligned} dp[i][0]dp[i][1]dp[i][2]=min(dp[i−1][1],dp[i−1][2])+costs[i][0]=min(dp[i−1][0],dp[i−1][2])+costs[i][1]=min(dp[i−1][0],dp[i−1][1])+costs[i][2]
The three color cases can be combined into one state transition equation,对于 1 ≤ i < n 1≤i<n 1≤i<n 和 0 ≤ j < 3 0≤j<3 0≤j<3,状态转移方程如下:
dp [ i ] [ j ] = min ( dp [ i − 1 ] [ ( j + 1 ) m o d 3 ] , \textit{dp}[i][j] = \min(\textit{dp}[i - 1][(j + 1) \bmod 3], dp[i][j]=min(dp[i−1][(j+1)mod3],
dp [ i − 1 ] [ ( j + 2 ) m o d 3 ] ) + costs [ i ] [ j ] \textit{dp}[i - 1][(j + 2) \bmod 3]) + \textit{costs}[i][j] dp[i−1][(j+2)mod3])+costs[i][j]
计算结束时, dp [ n − 1 ] \textit{dp}[n - 1] dp[n−1] The smallest of these is the minimum cost to paint all the houses.
当 i ≥ 1 i≥1 i≥1 时,由于 dp [ i ] \textit{dp}[i] dp[i]的计算只和 dp [ i − 1 ] \textit{dp}[i - 1] dp[i−1] 有关,So space can be optimized using rolling arrays,将空间复杂度降低到 O ( 1 ) O(1) O(1).
代码
class Solution:
def minCost(self, costs: List[List[int]]) -> int:
dp = costs[0]
for i in range(1, len(costs)):
dp = [min(dp[j - 1], dp[j - 2]) + c for j, c in enumerate(costs[i])]
return min(dp)
边栏推荐
猜你喜欢

More than pytorch from zero to build neural network to realize classification (training data sets)
Candide3人脸动画模型
OpenCV下载、安装以及使用
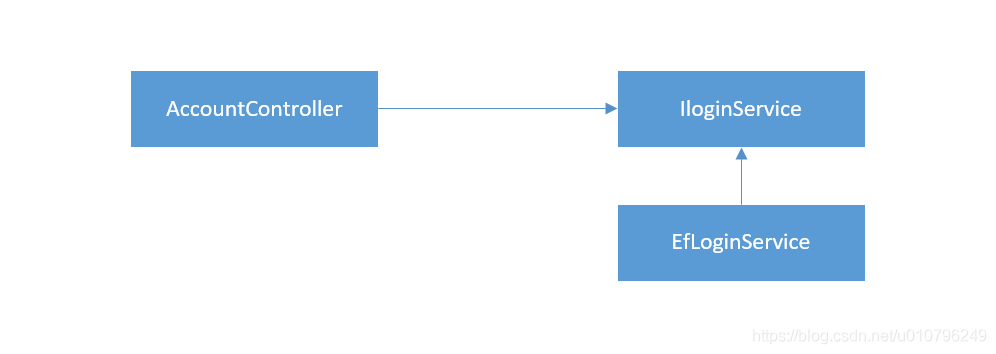
ASP.Net Core实战——初识.NetCore

类别特征编码分类任务选择及效果影响

Simply record offsetof and container_of

PHP开源 | ysKit(ys工具包) - 微型Web框架

【深度学习】介绍六大类损失函数(九)

ASP.Net Core实战——使用Swagger
It is deeply recognized that the compiler can cause differences in the compilation results
随机推荐
如何正确使用防关联浏览器
如何选择可靠的亚马逊代运营
关于初级程序员职场如何提升技能的几点建议?
Simply record offsetof and container_of
【研究生工作周报】(第八周)
抱抱脸(hugging face)教程-中文翻译-使用 AutoClass 加载预训练的实例
地铁预约Postman脚本使用
抱抱脸(hugging face)教程-中文翻译-基于pipeline的推理
抱抱脸(hugging face)教程-中文翻译-预处理
记一次解决Mysql:Incorrect string value: ‘\xF0\x9F\x8D\x83\xF0\x9F...‘ for column 插入emoji表情报错问题
Use tensorboard remotely on the server
function calling convention
PAT1027 Printing Hourglass
抱抱脸(hugging face)教程-中文翻译-分享一个模型
OpenCV下载、安装以及使用
A shortcut method for writing menu commands in C
【研究生工作周报】(第三周)
研究生工作周报(第四周)
C#轻量级ORM使用 Dapper+Contrib
实现一个支持请求失败后重试的JS方法
