当前位置:网站首页>【图形学】01 数学部分(一、集合和三角函数)
【图形学】01 数学部分(一、集合和三角函数)
2022-08-08 06:26:00 【纸境止境】
1、集合和映射(Sets and Mappings)
①当我们认为一个对象是一个集合的元素的时候,我们有:
a ∈ S a ∈ S a∈S
②当我们向创建第三个集合的时候,我们采用笛卡尔积(Cartesian product): A × B A × B A×B 。新的集合: A × B A × B A×B 包含了所有的有序 paris ( a , b ) ( a ∈ A & & b ∈ B ) (a, b)( a ∈ A \&\& b ∈ B) (a,b)(a∈A&&b∈B)
③常见的集合有:
④映射(Mapping): f f f 是一个从实数作为输入,映射到整数的函数。 f : R → Z , f : R → Z, f:R→Z, ,左边的我们称之为 作用域(domain),右边的我们称之为 值域(target)
⑤反函数(Inverse Mappings):如果我们有一个函数 f : A → B f : A → B f:A→B, 然后我们有一个反函数 f − 1 : B → A f^{−1} : B →A f−1:B→A。
⑥双射(bijections):一个双射函数形成一个对应,并且每一个输入值都有正好一个输出值以及每一个输出值都有正好一个输入值。
⑦交(∩,intersection)并(∪,unions)补(-,difference)
⑧对数(Logarithms): y = log a x ⇔ a y = x y\,\,=\,\,\log _ax\,\,⇔\,\,a^y=x y=logax⇔ay=x,其基本运算法则:
a l o g a ( x ) = x l o g a ( a x ) = x l o g a ( x y ) = l o g a x + l o g a y l o g a ( x / y ) = l o g a x − l o g a y l o g a x = l o g a b l o g b x a^{log_a\left( x \right)}=x \\ log_a\left( a^x \right) =x \\ log_a\left( xy \right) =log_ax\,\,+\,\,log_ay \\ log_a\left( x/y \right) =logax\,\,-\,\,logay \\ log_ax=log_ab\,\,log_bx aloga(x)=xloga(ax)=xloga(xy)=logax+logayloga(x/y)=logax−logaylogax=logablogbx
⑨弧度(radians):
d e g r e e s = 180 π r a d i a n s r a d i a n s = π 180 d e g r e e s degrees\,\,=\,\,\frac{180}{\pi}\,\,radians \\ radians\,\,=\,\,\frac{\pi}{180}\,\,degrees degrees=π180radiansradians=180πdegrees
2、三角函数公式:
基本变换:
s i n ( − A ) = − s i n A c o s ( − A ) = c o s A t a n ( − A ) = − t a n A s i n ( π / 2 − A ) = c o s A c o s ( π / 2 − A ) = s i n A t a n ( π / 2 − A ) = c o t A sin(−A) = −sinA \\ cos(−A) = cosA \\ tan(−A) = −tanA \\ sin(π/2 − A) = cosA \\ cos(π/2 − A) = sinA \\ tan(π/2 − A) = cotA sin(−A)=−sinAcos(−A)=cosAtan(−A)=−tanAsin(π/2−A)=cosAcos(π/2−A)=sinAtan(π/2−A)=cotA
平方变换:
s i n 2 A + c o s 2 A = 1 s e c 2 A − t a n 2 A = 1 c s c 2 A − c o t 2 A = 1 sin^2 A + cos^2 A = 1 \\ sec^2 A − tan^2 A = 1 \\ csc^2 A − cot^2 A = 1 sin2A+cos2A=1sec2A−tan2A=1csc2A−cot2A=1
加减变换:
s i n ( A + B ) = s i n A c o s B + s i n B c o s A s i n ( A − B ) = s i n A c o s B − s i n B c o s A s i n ( 2 A ) = 2 s i n A c o s A c o s ( A + B ) = c o s A c o s B − s i n A s i n B c o s ( A − B ) = c o s A c o s B + s i n A s i n B c o s ( 2 A ) = c o s 2 A − s i n 2 A t a n ( A + B ) = t a n A + t a n B 1 − t a n A t a n B t a n ( A − B ) = t a n A − t a n B 1 + t a n A t a n B t a n ( 2 A ) = 2 t a n A 1 − t a n 2 A sin(A + B) = sinA cosB + sinB cosA\\ sin(A − B) = sinA cosB − sinB cosA\\ sin(2A) = 2sinAcosA\\ cos(A + B) = cosA cosB − sinA sinB\\ cos(A − B) = cosA cosB + sinA sinB\\ cos(2A) = cos^2 A − sin^2 A\\ tan(A + B) =\frac{tanA + tanB}{1 − tanAtanB}\\ tan(A − B) =\frac{tanA − tanB}{1 + tanAtanB}\\ tan(2A) =\frac{2 tanA}{1 − tan2 A} sin(A+B)=sinAcosB+sinBcosAsin(A−B)=sinAcosB−sinBcosAsin(2A)=2sinAcosAcos(A+B)=cosAcosB−sinAsinBcos(A−B)=cosAcosB+sinAsinBcos(2A)=cos2A−sin2Atan(A+B)=1−tanAtanBtanA+tanBtan(A−B)=1+tanAtanBtanA−tanBtan(2A)=1−tan2A2tanA
Half-angle identities:
s i n 2 ( A / 2 ) = ( 1 − c o s A ) / 2 c o s 2 ( A / 2 ) = ( 1 + c o s A ) / 2 sin^2(A/2) = (1 − cosA)/2\\ cos^2(A/2) = (1 + cosA)/2 sin2(A/2)=(1−cosA)/2cos2(A/2)=(1+cosA)/2
Product identities:
s i n A s i n B = − ( c o s ( A + B ) − c o s ( A − B ) ) / 2 s i n A c o s B = ( s i n ( A + B ) + s i n ( A − B ) ) / 2 c o s A c o s B = ( c o s ( A + B ) + c o s ( A − B ) ) / 2 sinAsinB = −(cos(A + B) − cos(A − B))/2\\ sinAcosB= (sin(A + B) + sin(A − B))/2\\ cosAcosB= (cos(A + B) + cos(A − B))/2 sinAsinB=−(cos(A+B)−cos(A−B))/2sinAcosB=(sin(A+B)+sin(A−B))/2cosAcosB=(cos(A+B)+cos(A−B))/2
对于任意的三角形有:![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ePaGKoVy-1654065349920)(assets/image-20220311224729380.png)]](/img/ab/7c9904fcf13bbe749f62e43190a7d4.png)
边栏推荐
- Prompt for Extraction? PAIE:Prompting Arguement Interaction for Event Argument Extraction
- jupyter notebook添加目录
- ACM latex
- Unity—ParticleSystem (particle system) and Animator (animation state machine) batch manager
- Gym 101492E Teamwork 伪dp解法
- P20 美颜相机的实现——基础铺垫2
- 栈队列OJ题分享及讲解
- MongoDB配置文件.conf配置项介绍
- 神经网络二分类问题范例,神经网络解决分类问题
- MySQL数据库和数据表的增删改查基础
猜你喜欢

DesignWare_APB_GPIO模块DUT&Testbench仿真

Unity HDRP下VRTK传送、穿墙 时画面淡入淡出、视觉遮挡无法正确显示问题解决

cybox target machine wp

CSDN21天学习挑战赛之顺序查找

Mac下按装php的MongoDB扩展

Flutter 实现一款简单的音乐播放器
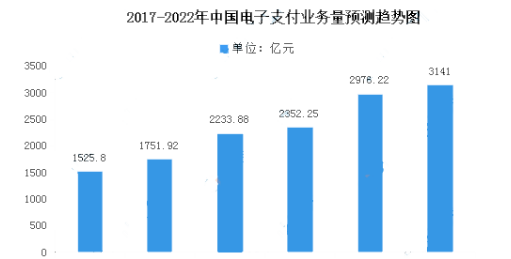
Electronic payment market status quo of the study: 2022 volume is expected to increase to 314.1 billion yuan

Unity 物体颜色渐变效果(判断逻辑实现)

简悦音乐播放器用到的相关技术点都在这里了(一)

最详细的Vivado安装教程
随机推荐
CSDN21天学习挑战赛之选择排序
二叉树代码练习
C# Unicode (Universal Code) text conversion
CSDN21天学习挑战赛之插入排序
Paramenter-Efficient Transfer Learning for NLP
人工神经网络的工作原理,神经网络的基本原理
Mac下按装php的MongoDB扩展
MongoDB配置文件.conf配置项介绍
bp神经网络预测模型原理,神经网络模型怎么预测
何恺明2017CVPR大会上演讲PPT,非常适合ResNet学习者!
状态机控制移位寄存器multisim仿真过程中出现的状态变量和状态转移条件不匹配的问题
简悦音乐播放器用到的相关技术点都在这里了(一)
leetcode每日一题8.6(持续更新)
Gym 101492E Teamwork 伪dp解法
神经网络的图像识别技术,神经网络的层数怎么看
CSDN21天学习挑战赛之顺序查找
Consumer Goods Industry Report: Research Analysis and Development Prospect Forecast of Cosmetic Container Market Status
MongoDB的备份与恢复
Yii2中对MongoDB的配置与问题处理
[Unity] GPU动画实现(四)——生成动画数据