Sort

Common sorting algorithms

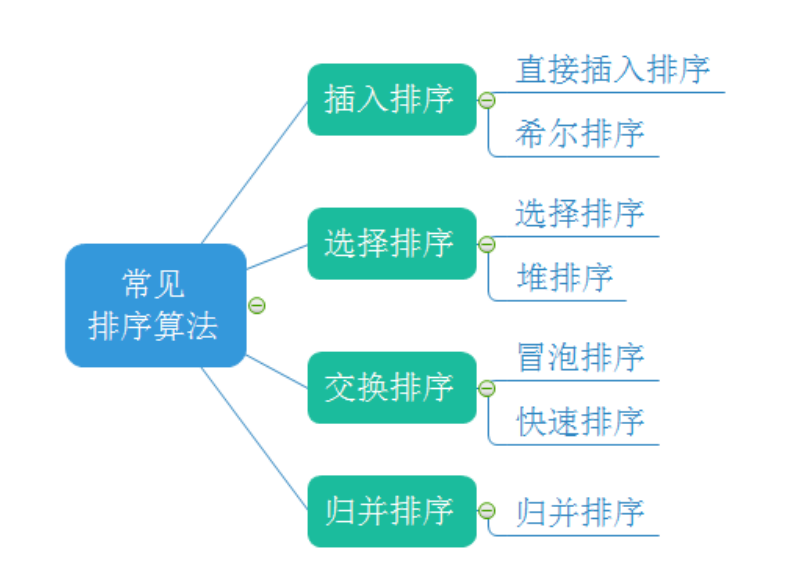
Implementation of common sorting algorithms

Merge sort

The basic idea

Merge sort （MERGE-SORT） It is an effective sorting algorithm based on merge operation , The algorithm is a divide-and-conquer method （Divide and Conquer） A very typical application . Merges ordered subsequences , You get a perfectly ordered sequence ; So let's make each subsequence in order , Then make the subsequence segments in order . If two ordered tables are merged into one ordered table , It's called a two-way merge . The core steps of merging and sorting ：

In fact, merging is not our first contact , We've been in contact before , such as Merge two ordered arrays This is the idea of merging

But our topic above is left interval order , The right interval is also ordered . Our normal questions will certainly not be given to you directly . This time a little deeper , Don't you have no order , Then let's divide , To the point that you can't share any more ,== That is, there is only one , Can you say that there is no order , Definitely not ==, So we continue to divide and conquer .

Recursive writing

Look at the above. GIF Also know that the first reaction is recursion

Check the phenomenon through debugging

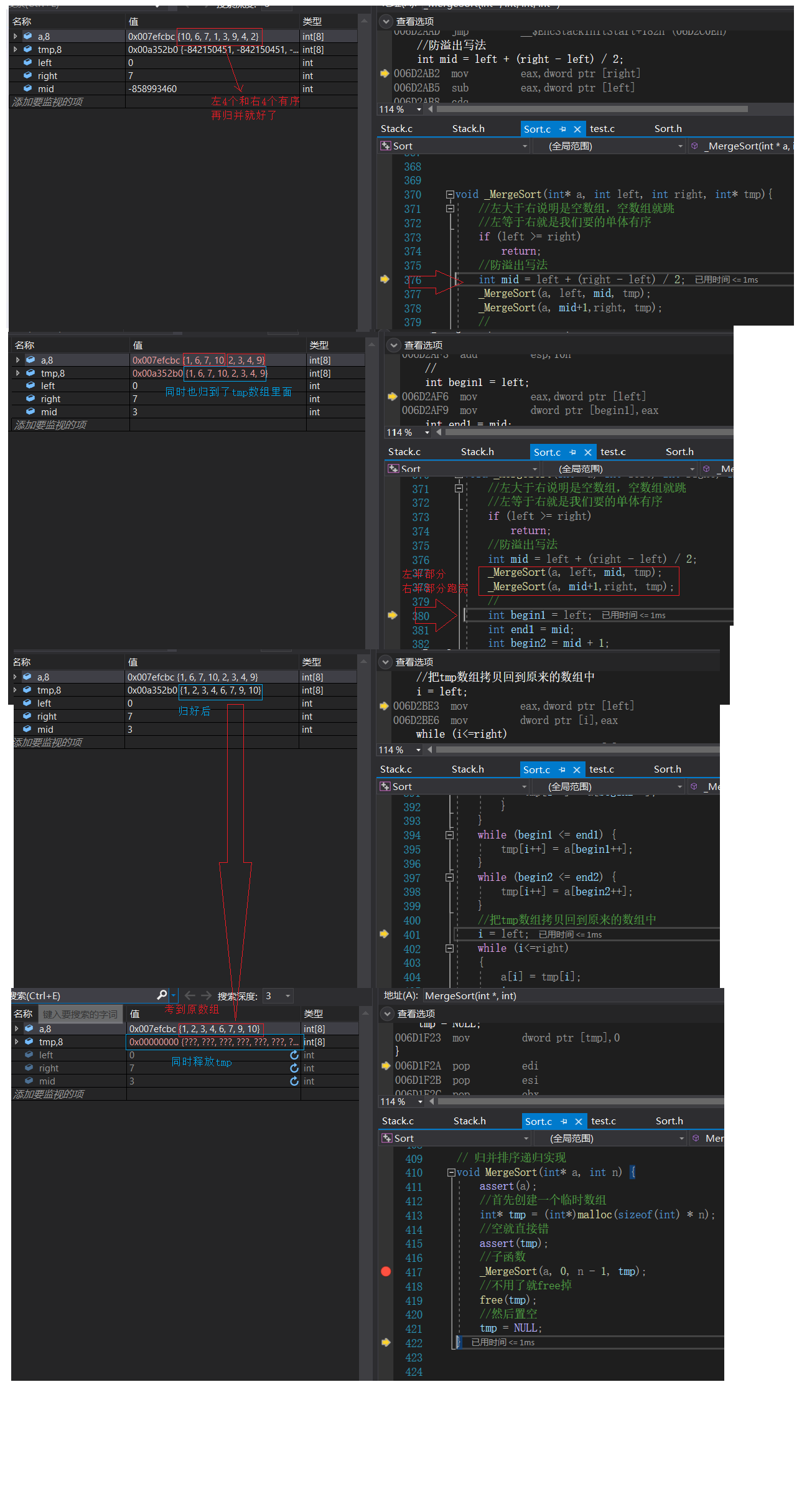
Merging order

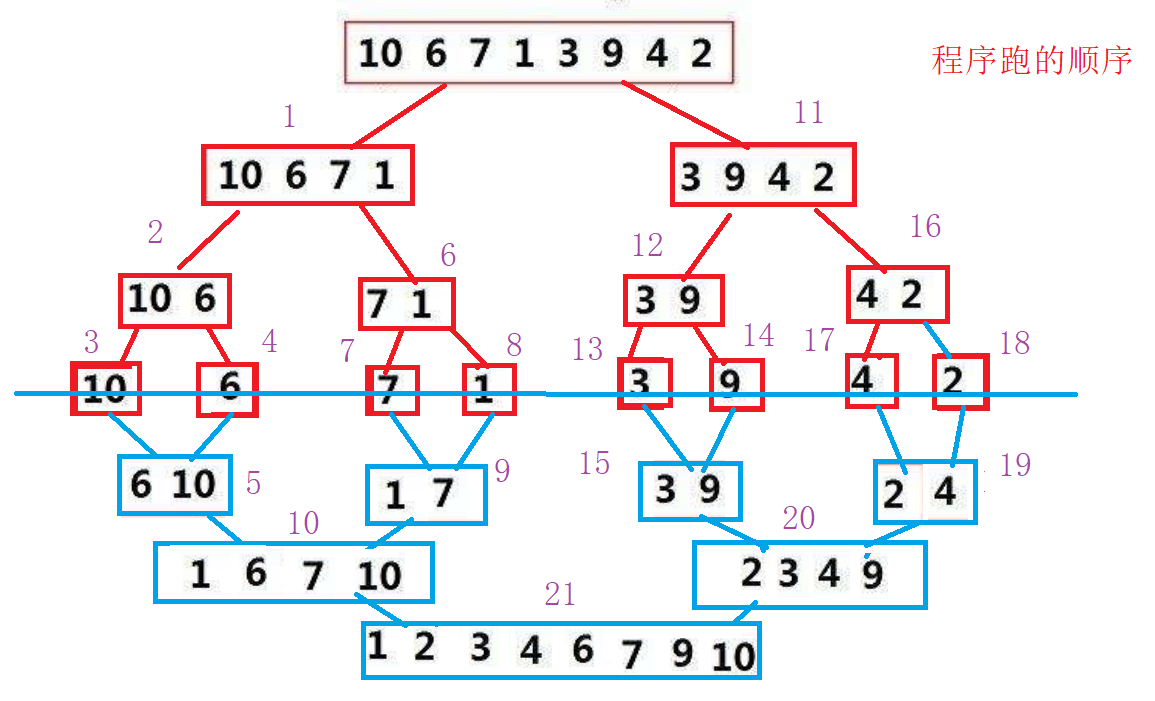
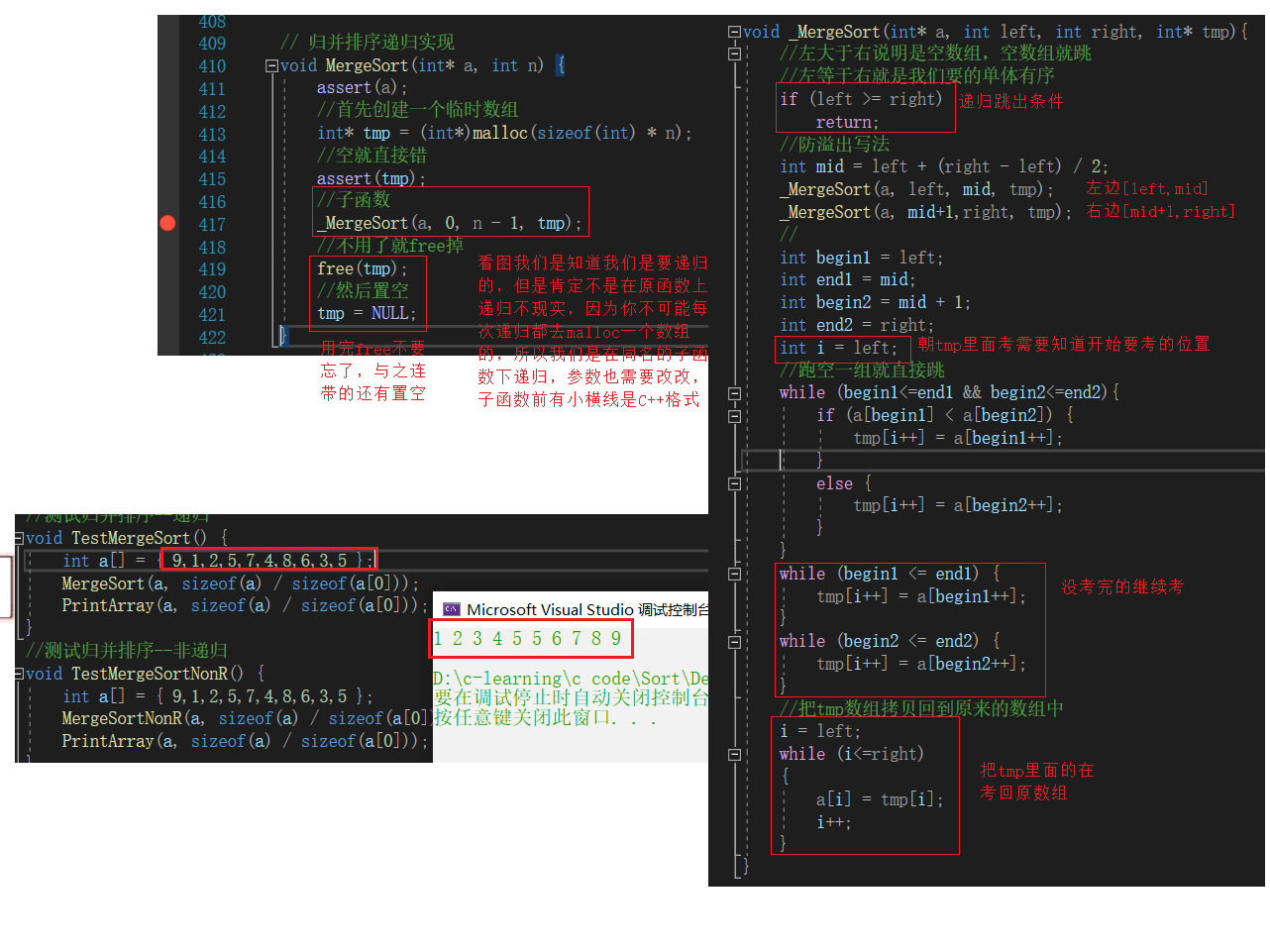
Merge sort recursive sub functions

//  Merge sort recursive sub functions void _MergeSort(int* a, int left, int right, int* tmp){	// If the left is greater than the right, it means that it is an empty array , Empty arrays jump 	// Left equals right, which is the monomer order we want 	if (left >= right)		return;	// Anti overflow writing 	int mid = left + (right - left) / 2;	_MergeSort(a, left, mid, tmp);	_MergeSort(a, mid+1,right, tmp);	//	int begin1 = left;	int end1 = mid;	int begin2 = mid + 1;	int end2 = right;	int i = left;	// Run empty group and jump directly 	while (begin1<=end1 && begin2<=end2){		if (a[begin1] < a[begin2]) {			tmp[i++] = a[begin1++];		}					else {			tmp[i++] = a[begin2++];		}	}	while (begin1 <= end1) {		tmp[i++] = a[begin1++];	}	while (begin2 <= end2) {		tmp[i++] = a[begin2++];	}	// hold tmp Copy the array back to the original array 	i = left;	while (i<=right)	{		a[i] = tmp[i];		i++;	}}

Merge sort recursive implementation

//  Merge sort recursive implementation void MergeSort(int* a, int n) {	assert(a);	// First create a temporary array 	int* tmp = (int*)malloc(sizeof(int) * n);	// Empty is directly wrong 	assert(tmp);	// Subfunctions 	_MergeSort(a, 0, n - 1, tmp);	// No, it's fine free fall 	free(tmp);	// Then leave it empty 	tmp = NULL;}

Non recursive writing

2^n^ Array of elements

We see there seems to be nothing wrong with it , That's used as the number of array elements. It's really good , There has been no single element , Well, it's not true

An array of any number of elements

Fixed subscript

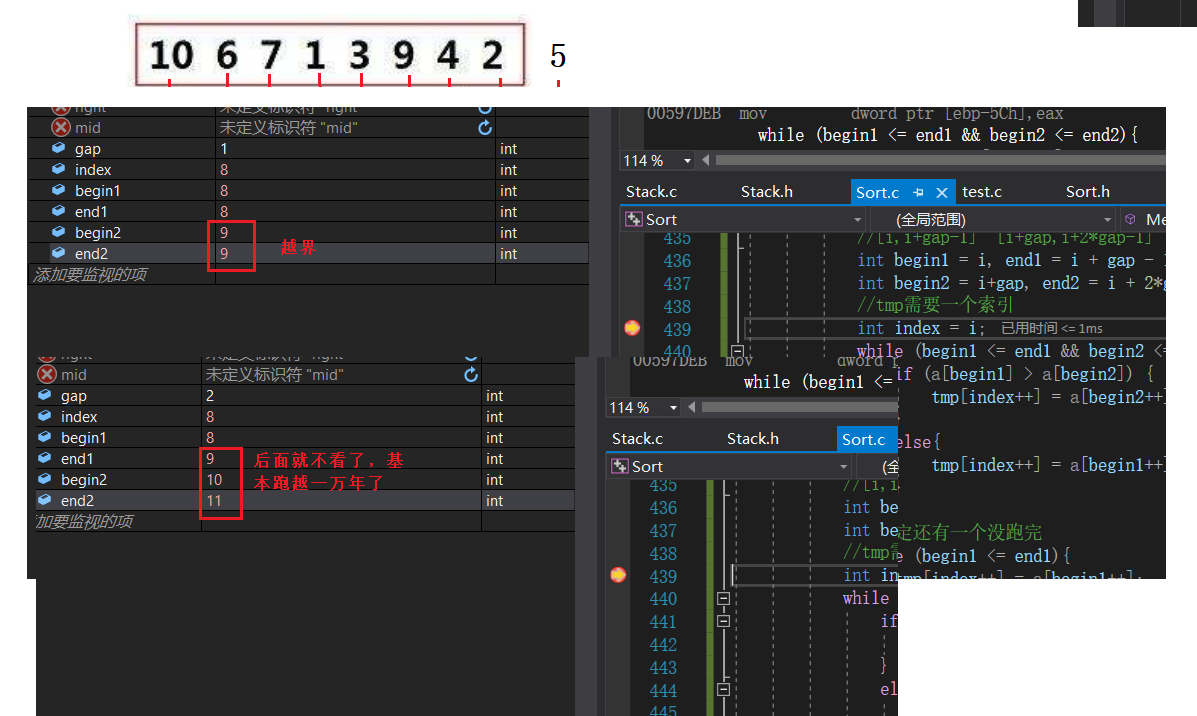
Cross border discussions

But there's another kind of nausea == Duplicate copy ==

So next we need to solve index problem

We revised it to n-1, You can also modify the array to be nonexistent , Let him not enter the following cycle, so he can not merge

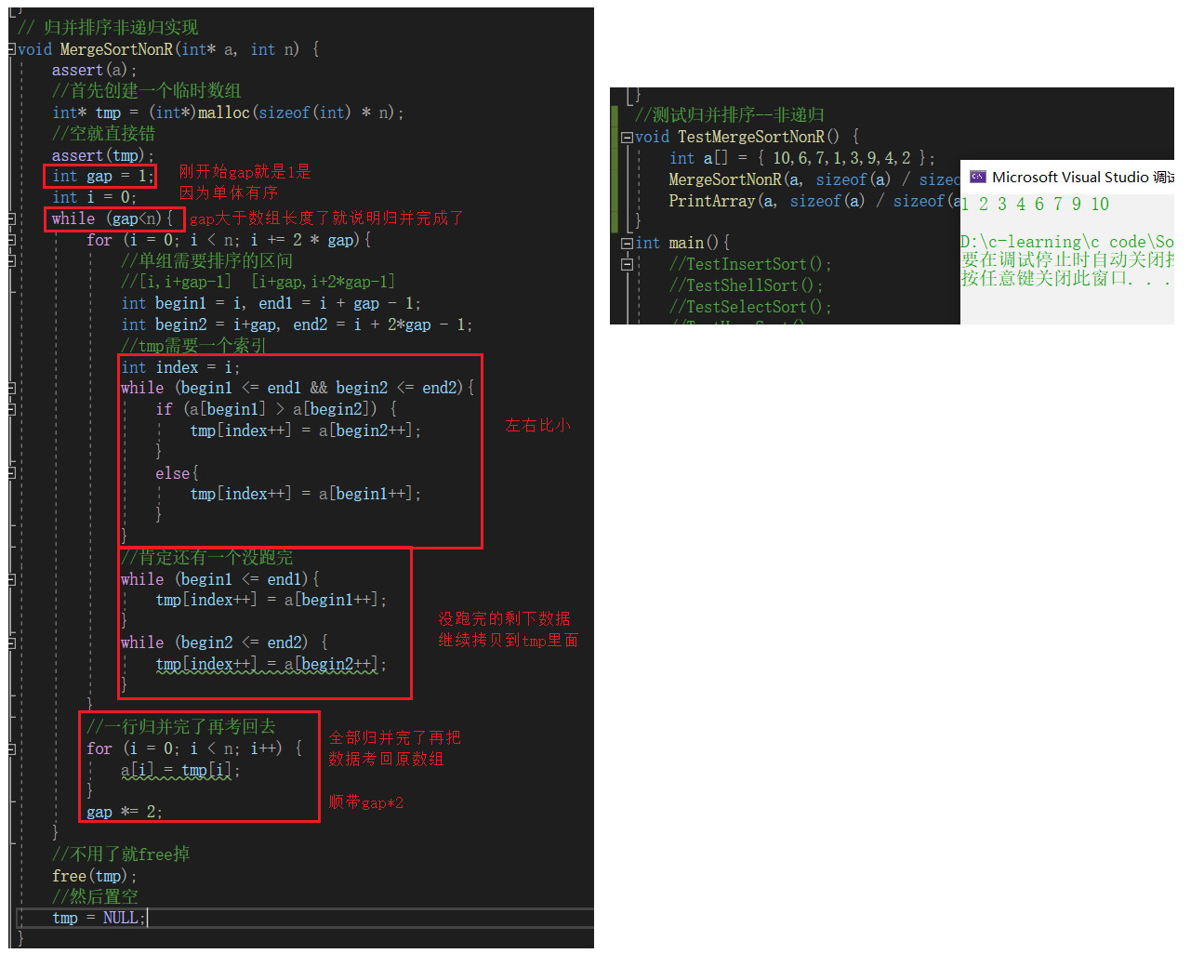
Merge sort non recursive implementation          Fixed subscript

//  Merge sort non recursive implementation void MergeSortNonR(int* a, int n) {	assert(a);	// First create a temporary array 	int* tmp = (int*)malloc(sizeof(int) * n);	// Empty is directly wrong 	assert(tmp);	int gap = 1;	int i = 0;	while (gap<n){		for (i = 0; i < n; i += 2 * gap){			// A single group of intervals to be sorted 			//[i,i+gap-1] [i+gap,i+2*gap-1]			int begin1 = i, end1 = i + gap - 1;			int begin2 = i+gap, end2 = i + 2*gap - 1;			// Applicable to the core part of any number of elements 			//end1 out ,[begin2,end2] non-existent 			if (end1 >= n) {				end1 = n - 1;			}			//[begin2,end2] non-existent 			if (begin2 >= n) {				begin2 = n ;				end2 = n - 1;			}			//end2 out 			if (end2 >= n) {				end2 = n - 1;			}			//printf("[%d,%d],[%d,%d]",begin1,end1,begin2,end2);			//// Duplicate copies are basically why we fix to the same location 			//// Let's talk about 			//if (begin1 == end1 && end1 == begin2 && begin2 == end2 && end2 == n-1)			//{			// // Any code to accept breakpoints , A fee code 			// int a = 0;			//}						//tmp Need an index 			int index = i;			while (begin1 <= end1 && begin2 <= end2){				if (a[begin1] > a[begin2]) {					tmp[index++] = a[begin2++];				}				else{					tmp[index++] = a[begin1++];				}			}						// There must be another one who hasn't finished 			while (begin1 <= end1){				tmp[index++] = a[begin1++];			}			while (begin2 <= end2) {				tmp[index++] = a[begin2++];			}					//printf(" %d", index);		}		//printf("\n");				// After a line is merged, go back to the exam 		for (i = 0; i < n; i++) {			a[i] = tmp[i];		}		gap *= 2;	}		// No, it's fine free fall 	free(tmp);	// Then leave it empty 	tmp = NULL;}

Part by part, part by part

We can also divide the copy into half and part like recursion , There's no need to fix it , Because many boundary conditions have to be considered in the correction , It's a bit tedious.

Merge sort non recursive implementation         Part by part, part by part

//  Merge sort non recursive implementation void MergeSortNonR(int* a, int n) {	assert(a);	// First create a temporary array 	int* tmp = (int*)malloc(sizeof(int) * n);	// Empty is directly wrong 	assert(tmp);	int gap = 1;	int i = 0;	while (gap<n){		for (i = 0; i < n; i += 2 * gap){			// A single group of intervals to be sorted 			//[i,i+gap-1] [i+gap,i+2*gap-1]			int begin1 = i, end1 = i + gap - 1;			int begin2 = i+gap, end2 = i + 2*gap - 1;			//// Applicable to the core part of any number of elements 			////end1 out ,[begin2,end2] non-existent 			//if (end1 >= n) {			// end1 = n - 1;			//}			////[begin2,end2] non-existent 			//if (begin2 >= n) {			// begin2 = n ;			// end2 = n - 1;			//}			////end2 out 			//if (end2 >= n) {			// end2 = n - 1;			//}			// Applicable to the core part of any number of elements 			//end1 out ,[begin2,end2] non-existent   There is no need to merge 			if (end1 >= n || begin2 >= n) {				// Jump directly , Because it is operated in the original array, there is no need to worry about the last one not being taken into account 				break;			}			//end2 out   Need to merge   On correction 			if (end2 >= n) {				end2 = n - 1;			}			//printf("[%d,%d],[%d,%d]",begin1,end1,begin2,end2);			//// Duplicate copies are basically why we fix to the same location 			//// Let's talk about 			//if (begin1 == end1 && end1 == begin2 && begin2 == end2 && end2 == n-1)			//{			// // Any code to accept breakpoints , A fee code 			// int a = 0;			//}						//tmp Need an index 			int index = i;			while (begin1 <= end1 && begin2 <= end2){				if (a[begin1] > a[begin2]) {					tmp[index++] = a[begin2++];				}				else{					tmp[index++] = a[begin1++];				}			}						// There must be another one who hasn't finished 			while (begin1 <= end1){				tmp[index++] = a[begin1++];			}			while (begin2 <= end2) {				tmp[index++] = a[begin2++];			}					// Copy one part of the file 			int j = 0;			for (j = i; j <= end2; j++) {				a[j] = tmp[j];			}			//printf(" %d", index);		}		//printf("\n");				//// After a line is merged, go back to the exam 		//for (i = 0; i < n; i++) {		// a[i] = tmp[i];		//}		gap *= 2;	}		// No, it's fine free fall 	free(tmp);	// Then leave it empty 	tmp = NULL;}

Summary of the characteristics of merge sorting

1. The disadvantage of merging is that it requires O(N) Spatial complexity of , The thinking of merge sort is more about solving the problem of external sort in disk .
2. Time complexity ：O(N*logN)
3. Spatial complexity ：O(N)
4. stability ： Stable

Time complexity

Time complexity :O(N*logN)

The method of merging and sorting is to put a group of n Sequence of Numbers , Split into two sequences , Then divide the two sequences , Keep dividing , Until divided into n A length of 1 Sequence . Then merge two by two . So again and again , Until the final form contains n An array of numbers .

== Total merge sort time = Decomposition time + The time when the subsequence is arranged + Merger time ==

No matter how many numbers each sequence has, it is a compromise decomposition , So the decomposition time is a constant , Negligible .

== be ： Total merge sort time = The time when the subsequence is arranged + Merger time ==

Test performance

1000    A thousand

10000    Ten thousand     == Abandon choice and bubbling first ==

100000    One hundred thousand           == Then discard the direct insertion ==

1000000    One million

10000000    Ten million

Code

Sort.h

#pragma once#include <stdio.h>#include <stdlib.h>#include <assert.h>#include <time.h>#define HEAP 1//  Interface for sorting implementation //  Print array extern void PrintArray(int* a, int n);//  Insertion sort extern void InsertSort(int* a, int n);//  Shell Sort extern void ShellSort(int* a, int n);// Data exchange extern void Swap(int* pa, int* pb);//  Selection sort extern void SelectSort(int* a, int n);// Downward adjustments extern void AdjustDwon(int* a, int n, int parent);//  Heap sort extern void HeapSort(int* a, int n);//  Bubble sort extern void BubbleSort(int* a, int n);//  Quick sort recursive implementation //  Quick sort hoare edition extern int PartSort1(int* a, int left, int right);//  Quick sort digging extern int PartSort2(int* a, int left, int right);//  Pointer before and after quick sort extern int PartSort3(int* a, int left, int right);extern void QuickSort(int* a, int left, int right);//  Quick sort   Non recursive implementation extern void QuickSortNonR(int* a, int left, int right);//  Merge sort recursive implementation extern void MergeSort(int* a, int n);//  Merge sort non recursive implementation extern void MergeSortNonR(int* a, int n);//  Count sorting extern void CountSort(int* a, int n);

Sort.c

#define _CRT_SECURE_NO_WARNINGS 1#include "Sort.h"#include"Stack.h"//  Print array void PrintArray(int* a, int n) {	assert(a);	int i = 0;	for (i = 0; i < n; i++) {		printf("%d ", a[i]);	}	printf("\n");}//  Insertion sort void InsertSort(int* a, int n) {	assert(a);	int i = 0;	for (i = 0; i < n - 1; i++)	{		int end = i;		int x = a[end+1];		while (end >= 0) {			// If the number to be inserted is smaller than the number in the sequence, prepare to move the position 			if (a[end] > x) {				a[end + 1] = a[end];				end--;			}			else {				// If the number inserted is larger than that in the order, jump out 				break;			}		}		// Jump out of two situations 		//1.end == -1  When 		//2.break  When 		// hold x to end Front one 		a[end + 1] = x;	}}//  Shell Sort void ShellSort(int* a, int n) {	// grouping 	int gap = n;	// Multiple pre sort （gap>1）+  Directly inserted into the （gap == 1）	while (gap>1){		//gap /= 2;		// Divided by three, we know we don't have to pass 1, So we +1 Let him have a must 1 Conditions 		gap = gap / 3 + 1;		// Single group lie more 		int i = 0;		for (i = 0; i < n - gap; i++) {		int end = i;		int x = a[end + gap];		while (end >= 0) {			if (a[end] > x) {				a[end + gap] = a[end];				// Step length is gap				end -= gap;			}			else {				break;			}		}		a[end + gap] = x;	}	}	}// Data exchange void Swap(int* pa, int* pb) {	int tmp = *pa;	*pa = *pb;	*pb = tmp;}//  Selection sort void SelectSort(int* a, int n) {	int begin = 0;	int end = n - 1;	while (begin < end){		// Single trip 		// The maximum number , The subscript of the lowest decimal 		int mini = begin;// Let's say the initial subscript 		int maxi = end;  // Let's assume that this is the subscript at the end 		int i = 0;		for (i = begin; i <= end; i++) {			if (a[i] < a[mini])				mini = i;			if (a[i] > a[maxi])				maxi = i;		}		// The smallest one is in the front 		Swap(&a[begin], &a[mini]);				if (begin == maxi)			// If the maximum number is begin Positional , Then when exchanging, the maximum number moves with the subscript 			maxi = mini;		// Put the biggest one in the back 		Swap(&a[end], &a[maxi]);		begin++;		end--;	}}// Adjust the function down void AdjustDown(int* a, int n, int parent){	assert(a);	// Create a child variable , Two children add... To this 1 Just go 	int child = parent * 2 + 1;#if HEAP	while (child < n)	{		// Choose older children 		if (child + 1 < n && a[child] < a[child + 1])		{			child++;		}		// Older children exchange when they are older than their father 		if (a[child] > a[parent])		{			Swap(&a[child], &a[parent]);			parent = child;			child = parent * 2 + 1;		}		else		{			break;		}	}#elif !HEAP	while (child < n)	{		// Choose children 		if (child + 1 < n && a[child] > a[child + 1])		{			child++;		}		// Young children exchange when they are younger than their father 		if (a[child] < a[parent])		{			Swap(&a[child], &a[parent]);			parent = child;			child = parent * 2 + 1;		}		else		{			break;		}	}#endif // HEAP }//  Heap sort   We talked about building a lot in ascending order before void HeapSort(int* a, int n) {	// Reactor building time complexity O(N)	// Build a pile 	int i = 0;	for (i = (n - 1 - 1) / 2; i >= 0; i--) {		AdjustDown(a, n, i);	}	int end = n - 1;	// Heap sort time complexity O(N*logN)	while (end>0){		// In exchange for   Put the biggest back 		Swap(&a[0], &a[end]);		// Adjust down 		AdjustDown(a,end,0);		end--;	}}//  Bubble sort void BubbleSort(int* a, int n) {	// Lie more 	int j = 0;		for (j = 0; j < n - 1; j++) {			// Swap tag variables 		int flag = 0;		// Single trip 		int i = 0;		for (i = 0; i < n - 1-j; i++) {						if (a[i] > a[i + 1]) {				// Exchange mark change 				flag = 1;				Swap(&a[i], &a[i + 1]);			}		}		// Mark or 0 Just jump out 		if (!flag)			break;	}}// Take the three Numbers int GetMinIndex(int* a, int left, int right) {	// This will prevent  int  overflow 	int mid = left + (right - left) / 2;	if (a[left] < a[mid]) {		if (a[mid] < a[right])			return mid;		else if (a[left] > a[right])			return left;		else			return right;	}	else //a[left] >= a[mid]	{		if (a[mid] > a[right])			return mid;		else if (a[left] < a[right])			return left;		else			return right;	}}//  Quick sort hoare edition   Single pass sorting // Leftmost do key [left,right]  Let's give you an interval here int PartSort1(int* a, int left, int right) {	// Take the three Numbers 	int mini = GetMinIndex(a, left, right);	// Put the middle number to the far left , In exchange 	Swap(&a[mini], &a[left]);	// Or on the far left keyi	int keyi = left;	// Stop when you meet left and right 	while (left < right)	{		// On the far left is key, Then move first on the far right 		// Find less than key Of 		while (left < right && a[right] >= a[keyi]) {			right--;		}		// Then move the right 		// Find more than key Of 		while (left < right && a[left] <= a[keyi]) {			left++;		}		Swap(&a[left], &a[right]);	}	Swap(&a[keyi], &a[right]);	// After returning to the correct position keyi	return left;}//  Quick sort digging int PartSort2(int* a, int left, int right) {	assert(a);	// Take the three Numbers 	int mini = GetMinIndex(a, left, right);	// Put the middle number to the far left , In exchange 	Swap(&a[mini], &a[left]);	// The first Key Save it 	int Key = a[left];	// Dig a hole 	int pit = left;	while (left<right){		// Look for a small on the right 		while (left < right && a[right] >= Key) {			right--;		}		// Throw the data into the pit when you find it 		Swap(&a[right],&a[pit]);		// You become a new pit 		pit = right;		// Look big on the left 		while (left < right && a[left] <= Key) {			left++;		}		// Throw the data into the pit when you find it 		Swap(&a[left], &a[pit]);		// You become a new pit 		pit = left;	}	// When you come out, put Key Put it in the pit 	a[pit] = Key;	return pit;}//  Pointer before and after quick sort int PartSort3(int* a, int left, int right) {	assert(a);		// Take the three Numbers 	int mini = GetMinIndex(a, left, right);	// Put the middle number to the far left , In exchange 	Swap(&a[mini], &a[left]);	// hold keyi write down 	int keyi = left;	int prev = left;	int cur = prev + 1;	while (cur <= right){		//// Than Key Jump out when you're young 		//while (cur <= right && a[cur] >= a[keyi]) {		// cur++;		//}		//if (cur <= right) {		// // Jump out prev++		// prev++;		// // In exchange for 		// Swap(&a[prev], &a[cur]);		// // After the exchange cur also ++		// cur++;		//} 		if(a[cur] < a[keyi])			Swap(&a[prev++], &a[cur]);		cur++;	}	// Jump out to explain the exchange a[prev] and Key	Swap(&a[prev],&a[keyi]);	return prev;}//  Quick sort   Inter cell optimization void QuickSort(int* a, int left, int right) {	if (left >= right)		return;	if (right - left + 1 < 10)//10 Insert a number within 	{		InsertSort(a + left, right - left + 1);	}	else	{		int keyi = PartSort3(a, left, right);		//[left,keyi-1] keyi [keyi+1,right]		QuickSort(a, left, keyi - 1);		QuickSort(a, keyi + 1, right);	}	}//  Quick sort   Non recursive implementation void QuickSortNonR(int* a, int left, int right) {	// Build a stack 	ST st;	// Initialization stack 	StackInit(&st);	//left Into the stack 	StackPush(&st, left);	//right Into the stack 	StackPush(&st, right);	// Empty stack jumps out  	while (!StackEmpty(&st))	{		// Take the tail first 		int end = StackTop(&st);		//pop fall 		StackPop(&st);		// Then take the head 		int start = StackTop(&st);		// Again pop fall 		StackPop(&st);		// Then, sort in a single pass to find keyi		int keyi = PartSort3(a,start,end);		//[start,keyi-1] keyi [keyi+1,end]		if (keyi + 1 < end)// Indicates that the separated interval is greater than 1		{			// Because we take the tail first , So ask first 			StackPush(&st, keyi + 1);			// Reentry tail 			StackPush(&st, end);		}		if (keyi - 1 > start)// Indicates that the separated interval is greater than 1		{			// Because we take the tail first , So ask first 			StackPush(&st, start);			// Reentry tail 			StackPush(&st, keyi - 1);		}	}	// Stack destruction linked with initialization 	StackDestroy(&st);}//  Merge sort recursive sub functions void _MergeSort(int* a, int left, int right, int* tmp){	// If the left is greater than the right, it means that it is an empty array , Empty arrays jump 	// Left equals right, which is the monomer order we want 	if (left >= right)		return;	// Anti overflow writing 	int mid = left + (right - left) / 2;	_MergeSort(a, left, mid, tmp);	_MergeSort(a, mid+1,right, tmp);	//	int begin1 = left;	int end1 = mid;	int begin2 = mid + 1;	int end2 = right;	int i = left;	// Run empty group and jump directly 	while (begin1<=end1 && begin2<=end2){		if (a[begin1] < a[begin2]) {			tmp[i++] = a[begin1++];		}					else {			tmp[i++] = a[begin2++];		}	}	while (begin1 <= end1) {		tmp[i++] = a[begin1++];	}	while (begin2 <= end2) {		tmp[i++] = a[begin2++];	}	// hold tmp Copy the array back to the original array 	i = left;	while (i<=right)	{		a[i] = tmp[i];		i++;	}}//  Merge sort recursive implementation void MergeSort(int* a, int n) {	assert(a);	// First create a temporary array 	int* tmp = (int*)malloc(sizeof(int) * n);	// Empty is directly wrong 	assert(tmp);	// Subfunctions 	_MergeSort(a, 0, n - 1, tmp);	// No, it's fine free fall 	free(tmp);	// Then leave it empty 	tmp = NULL;}//  Merge sort non recursive implementation void MergeSortNonR(int* a, int n) {	assert(a);	// First create a temporary array 	int* tmp = (int*)malloc(sizeof(int) * n);	// Empty is directly wrong 	assert(tmp);	int gap = 1;	int i = 0;	while (gap<n){		for (i = 0; i < n; i += 2 * gap){			// A single group of intervals to be sorted 			//[i,i+gap-1] [i+gap,i+2*gap-1]			int begin1 = i, end1 = i + gap - 1;			int begin2 = i+gap, end2 = i + 2*gap - 1;			//// Applicable to the core part of any number of elements 			////end1 out ,[begin2,end2] non-existent 			//if (end1 >= n) {			// end1 = n - 1;			//}			////[begin2,end2] non-existent 			//if (begin2 >= n) {			// begin2 = n ;			// end2 = n - 1;			//}			////end2 out 			//if (end2 >= n) {			// end2 = n - 1;			//}			// Applicable to the core part of any number of elements 			//end1 out ,[begin2,end2] non-existent   There is no need to merge 			if (end1 >= n || begin2 >= n) {				// Jump directly , Because it is operated in the original array, there is no need to worry about the last one not being taken into account 				break;			}			//end2 out   Need to merge   On correction 			if (end2 >= n) {				end2 = n - 1;			}			//printf("[%d,%d],[%d,%d]",begin1,end1,begin2,end2);			//// Duplicate copies are basically why we fix to the same location 			//// Let's talk about 			//if (begin1 == end1 && end1 == begin2 && begin2 == end2 && end2 == n-1)			//{			// // Any code to accept breakpoints , A fee code 			// int a = 0;			//}						//tmp Need an index 			int index = i;			while (begin1 <= end1 && begin2 <= end2){				if (a[begin1] > a[begin2]) {					tmp[index++] = a[begin2++];				}				else{					tmp[index++] = a[begin1++];				}			}						// There must be another one who hasn't finished 			while (begin1 <= end1){				tmp[index++] = a[begin1++];			}			while (begin2 <= end2) {				tmp[index++] = a[begin2++];			}					// Copy one part of the file 			int j = 0;			for (j = i; j <= end2; j++) {				a[j] = tmp[j];			}			//printf(" %d", index);		}		//printf("\n");				//// After a line is merged, go back to the exam 		//for (i = 0; i < n; i++) {		// a[i] = tmp[i];		//}		gap *= 2;	}		// No, it's fine free fall 	free(tmp);	// Then leave it empty 	tmp = NULL;}

test.c

#define _CRT_SECURE_NO_WARNINGS 1#include "Sort.h"//  Test the performance comparison of sorting void TestOP(){	// Set a random starting point 	srand(time(NULL));	// The size of the array to be created 	const int N = 10000000;	int* a1 = (int*)malloc(sizeof(int) * N);	int* a2 = (int*)malloc(sizeof(int) * N);	int* a3 = (int*)malloc(sizeof(int) * N);	int* a4 = (int*)malloc(sizeof(int) * N);	int* a5 = (int*)malloc(sizeof(int) * N);	int* a6 = (int*)malloc(sizeof(int) * N);	int* a7 = (int*)malloc(sizeof(int) * N);	int* a8 = (int*)malloc(sizeof(int) * N);	int* a9 = (int*)malloc(sizeof(int) * N);	for (int i = 0; i < N; ++i)	{		// Ensure that the two arrays are the same 		a1[i] = rand();		a2[i] = a1[i];		a3[i] = a1[i];		a4[i] = a1[i];		a5[i] = a1[i];		a6[i] = a1[i];		a7[i] = a1[i];		a8[i] = a1[i];		a9[i] = a1[i];	}	int begin1 = clock();// Starting time 	//InsertSort(a1, N);	int end1 = clock();  // End time 	int begin2 = clock();	ShellSort(a2, N);	int end2 = clock();	int begin3 = clock();	//SelectSort(a3, N);	int end3 = clock();	int begin4 = clock();	HeapSort(a4, N);	int end4 = clock();	int begin5 = clock();	//BubbleSort(a5, N);	int end5 = clock();	int begin6 = clock();	QuickSort(a6, 0, N - 1);	int end6 = clock();	int begin7 = clock();	QuickSortNonR(a7, 0, N - 1);	int end7 = clock();	int begin8 = clock();	MergeSort(a8, N);	int end8 = clock();	int begin9 = clock();	MergeSort(a9, N);	int end9 = clock();	printf("InsertSort:%d\n", end1 - begin1);// End time minus start time  	printf("ShellSort:%d\n", end2 - begin2);	printf("SelectSort:%d\n", end3 - begin3);	printf("HeapSort:%d\n", end4 - begin4);	printf("BubbleSort:%d\n", end5 - begin5);	printf("QuickSort:%d\n", end6 - begin6);	printf("QuickSortNonR:%d\n", end7 - begin7);	printf("MergeSort:%d\n", end8 - begin8);	printf("MergeSortNonR:%d\n", end9 - begin9);	free(a1);	free(a2);	free(a3);	free(a4);	free(a5);	free(a6);	free(a7);	free(a8);	free(a9);}// Test insert sort void TestInsertSort() {	int a[] = { 1,5,3,7,0,9 };	InsertSort(a, sizeof(a) / sizeof(a[0]));		PrintArray(a, sizeof(a) / sizeof(a[0]));}// Test Hill sort void TestShellSort() {	int a[] = { 9,1,2,5,7,4,8,6,3,5 };	ShellSort(a, sizeof(a) / sizeof(a[0]));	PrintArray(a, sizeof(a) / sizeof(a[0]));}// Test selection sort void TestSelectSort() {	int a[] = { 9,1,2,5,7,4,8,6,3,5 };	SelectSort(a, sizeof(a) / sizeof(a[0]));	PrintArray(a, sizeof(a) / sizeof(a[0]));}// Test heap sorting void TestHeapSort() {	int a[] = { 9,1,2,5,7,4,8,6,3,5 };	HeapSort(a, sizeof(a) / sizeof(a[0]));	PrintArray(a, sizeof(a) / sizeof(a[0]));}// Test bubble sort void TestBubbleSort() {	int a[] = { 9,1,2,5,7,4,8,6,3,5 };	BubbleSort(a, sizeof(a) / sizeof(a[0]));	PrintArray(a, sizeof(a) / sizeof(a[0]));}// Test single pass sorting void TestPartSort1() {	int a[] = { 5,5,5,5,5,5,5,5,5,5 };	PartSort1(a,0 ,sizeof(a) / sizeof(a[0])-1);	PrintArray(a, sizeof(a) / sizeof(a[0]));}// Test quick sort void TestQuickSort() {	int a[] = { 9,1,2,5,7,4,8,6,3,5 };	QuickSort(a, 0, sizeof(a) / sizeof(a[0]) - 1);	PrintArray(a, sizeof(a) / sizeof(a[0]));}// Test quick sort -- Non recursive void TestQuickSortNonR() {	int a[] = { 9,1,2,5,7,4,8,6,3,5 };	QuickSortNonR(a, 0, sizeof(a) / sizeof(a[0]) - 1);	PrintArray(a, sizeof(a) / sizeof(a[0]));}// Test merge sort -- recursive void TestMergeSort() {	int a[] = { 10,6,7,1,3,9,4,2 };	MergeSort(a, sizeof(a) / sizeof(a[0]));	PrintArray(a, sizeof(a) / sizeof(a[0]));}// Test merge sort -- Non recursive void TestMergeSortNonR() {	int a[] = {  10,6,7,1,3,9,4,2,5 };	MergeSortNonR(a, sizeof(a) / sizeof(a[0]));	PrintArray(a, sizeof(a) / sizeof(a[0]));}int main(){	//TestInsertSort();	//TestShellSort();	//TestSelectSort();	//TestHeapSort();	//TestBubbleSort();	//TestPartSort1();	//TestQuickSort();	//TestQuickSortNonR();	//TestMergeSort();	//TestMergeSortNonR();	TestOP();	return 0;}