前言

如果看过前面这几篇，那么下面这几题，应该不在话下

深入理解二叉树的前中后序

104二叉树的最大深度，543二叉树的直径，124二叉树的最大路径和

226翻转二叉树，116填充二叉树节点的右侧指针，114将二叉树展开为链表

先来复习一下，我们说过写树的算法，关键思路如下：

把题目的要求细化，搞清楚根节点应该做什么，然后剩下的事情交给前/中/后序的遍历框架就行了，千万不要跳进递归的细节里，因为很烧脑。

654. 最大二叉树

654. 最大二叉树，leetcode链接

函数签名如下：

public TreeNode constructMaximumBinaryTree(int[] nums) {
    };

按照我们刚刚说的，先明确根节点做什么？

对于构造二叉树的问题，根节点要做的就是想办法把自己构造出来。

我们肯定要遍历数组找到最大值maxVal，把根节点root做出来，然后对maxVal左边的数组和右边的数组进行递归调用，作为root的左右子树。

按照题目给出的例子，输入的数组为[3,2,1,6,0,5]，对于整棵树的根节点来说，其实在做这件事：

TreeNode constructMaximumBinaryTree([3,2,1,6,0,5]) {
    
    // 找到数组中的最大值
    TreeNode root = new TreeNode(6);
    // 递归调用构造左右子树
    root.left = constructMaximumBinaryTree([3,2,1]);
    root.right = constructMaximumBinaryTree([0,5]);
    return root;
}

再详细一点，就是如下伪码：

TreeNode constructMaximumBinaryTree(int[] nums) {
    
    if (nums is empty) return null;
    // 找到数组中的最大值,和对应的索引
    int maxVal = Integer.MIN_VALUE;
    int index = 0;
    for (int i = 0; i < nums.length; i++) {
    
        if (nums[i] > maxVal) {
    
            maxVal = nums[i];
            index = i;
        }
    }

    TreeNode root = new TreeNode(maxVal);
    // 递归调用构造左右子树
    root.left = constructMaximumBinaryTree(nums[0..index-1]);
    root.right = constructMaximumBinaryTree(nums[index+1..nums.length-1]);
    return root;
}

你看，对于每个根节点，只需要找到当前nums中的最大值和对应的索引，然后递归调用左右数组构造左右子树就行啦。

好，明确了思路，我们可以重新写一个辅助函数build，来控制nums的索引：

/* 主函数 */
TreeNode constructMaximumBinaryTree(int[] nums) {
    
    return build(nums, 0, nums.length - 1);
}

/* 将 nums[l...r] 构造成符合条件的树，返回根节点 */
TreeNode build(int[] nums, int l, int r) {
    
    // base case
    if (l > r) {
    
        return null;
    }

    // 找到数组中的最大值和对应的索引
    int index = -1, maxVal = Integer.MIN_VALUE;
    for (int i = l; i <= r; i++) {
    
        if (maxVal < nums[i]) {
    
            index = i;
            maxVal = nums[i];
        }
    }

    TreeNode root = new TreeNode(maxVal);
    // 递归调用构造左右子树
    root.left = build(nums, l, index - 1);
    root.right = build(nums, index + 1, r);

    return root;
}

105. 根据前序与中序遍历构造二叉树

105. 从前序与中序遍历序列构造二叉树，leetcode链接

函数签名如下：

public TreeNode buildTree(int[] preorder, int[] inorder) {
    };

还是一样，首先思考，根节点应该做什么。

类似前一题，我们肯定要想办法确定根节点的值，把根节点做出来，然后递归构造左右子树即可。

我们先来回顾一下，前序遍历和中序遍历的结果有什么特点？

了解二叉树前中后序遍历，找到根节点应该是比较简单的，前序遍历的第一个值preorder[0]就是根节点的值，关键是，如何通过根节点的值，将preorder和postorder数组划分成两半，构造根节点的左右子树？

换句话说，对于以下代码中的?部分应该填入什么：

/* 主函数 */
TreeNode buildTree(int[] preorder, int[] inorder) {
    

    return build(preorder, 0, preorder.length - 1,
                 inorder, 0, inorder.length - 1);
}

/* 前序遍历数组为 preorder[preStart...preEnd]， 中序遍历数组为 inorder[inStart...inEnd]， 构造二叉树，返回该二叉树的根节点 */
TreeNode build(int[] preorder, int preStart, int preEnd, 
               int[] inorder, int inStart, int inEnd) {
    
    // root 节点对应的值就是前序遍历数组的第一个元素
    int rootVal = preorder[preStart];
    // rootVal 在中序遍历数组中的索引
    int index = 0;
    for (int i = inStart; i <= inEnd; i++) {
    
        if (inorder[i] == rootVal) {
    
            index = i;
            break;
        }
    }
	// 构造跟节点
    TreeNode root = new TreeNode(rootVal);
    // 递归构造左右子树
    root.left = build(preorder, ?, ?,
                      inorder, ?, ?);

    root.right = build(preorder, ?, ?,
                       inorder, ?, ?);
    return root;
}

对于代码中的rootVal和index变量，就是下图这种情况：

现在我们来看图做填空题，下面这几个问号处应该填什么：

root.left = build(preorder, ?, ?,
                  inorder, ?, ?);

root.right = build(preorder, ?, ?,
                   inorder, ?, ?);

对于左右子树，对应的inorder数组的起始索引和终止索引比较容易确定：

root.left = build(preorder, ?, ?,
                  inorder, inStart, index - 1);

root.right = build(preorder, ?, ?,
                   inorder, index + 1, inEnd);

对于preorder数组呢？如何确定左右数组对应的起始索引和终止索引？

这个可以通过左子树的节点数推导出来，假设左子树的节点数为leftSize，那么preorder数组上的索引情况是这样的：

看着d上图就可以把preorder对应的索引写进去了：

int leftSize = index - inStart;

root.left = build(preorder, preStart + 1, preStart + leftSize,
                  inorder, inStart, index - 1);

root.right = build(preorder, preStart + leftSize + 1, preEnd,
                   inorder, index + 1, inEnd);

至此，整个算法思路就完成了，我们再补一补 base case 即可写出解法代码：

TreeNode build(int[] preorder, int preStart, int preEnd, 
               int[] inorder, int inStart, int inEnd) {
    

    if (preStart > preEnd) {
    
        return null;
    }

    // root 节点对应的值就是前序遍历数组的第一个元素
    int rootVal = preorder[preStart];
    // rootVal 在中序遍历数组中的索引
    int index = 0;
    for (int i = inStart; i <= inEnd; i++) {
    
        if (inorder[i] == rootVal) {
    
            index = i;
            break;
        }
    }

    int leftSize = index - inStart;

    // 先构造出当前根节点
    TreeNode root = new TreeNode(rootVal);
    // 递归构造左右子树
    root.left = build(preorder, preStart + 1, preStart + leftSize,
                      inorder, inStart, index - 1);

    root.right = build(preorder, preStart + leftSize + 1, preEnd,
                       inorder, index + 1, inEnd);
    return root;
}

看着build函数这么多参数，解法这么多代码，感觉很难。。。但实际上，你仔细思考下，与上面那题的本质逻辑是一样的，这些参数无非就是控制数组起止位置的。

106. 根据中序与后序遍列构造二叉树

106. 从中序与后序遍历序列构造二叉树，leetcode链接

函数签名如下：

public TreeNode buildTree(int[] inorder, int[] postorder) {
    };

类似的，知道了后序遍历和中序遍历的特点，这样的遍历顺序差异，导致了preorder和inorder数组中的元素分布有如下特点：

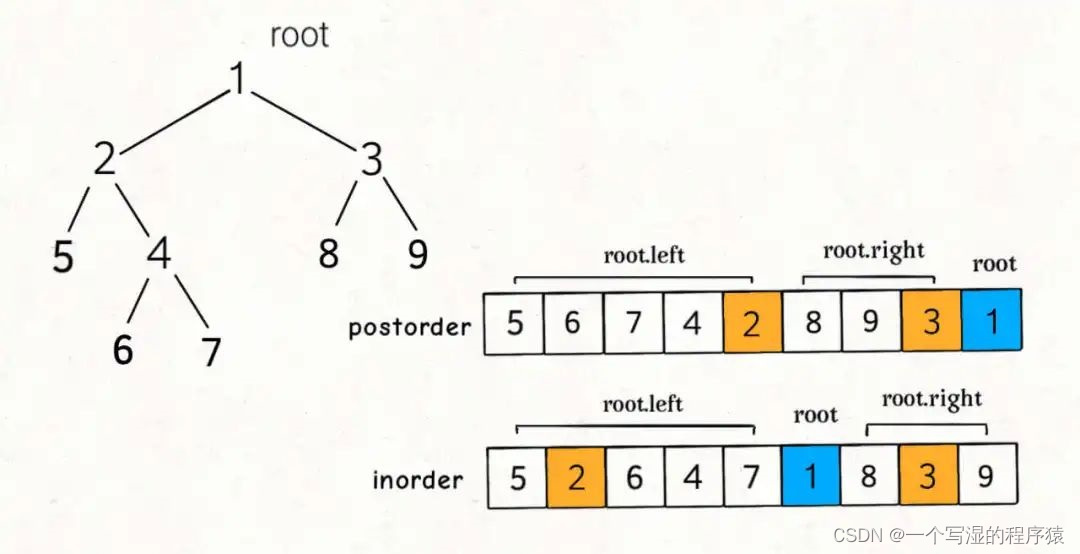
这道题和上一题的关键区别是，后序遍历和前序遍历相反，根节点对应的值为postorder的最后一个元素。

整体的算法框架和上一题非常类似，我们依然写一个辅助函数build：

TreeNode buildTree(int[] inorder, int[] postorder) {
    
    return build(inorder, 0, inorder.length - 1,
                 postorder, 0, postorder.length - 1);
}

TreeNode build(int[] inorder, int inStart, int inEnd,
               int[] postorder, int postStart, int postEnd) {
    
    // root 节点对应的值就是后序遍历数组的最后一个元素
    int rootVal = postorder[postEnd];
    // rootVal 在中序遍历数组中的索引
    int index = 0;
    for (int i = inStart; i <= inEnd; i++) {
    
        if (inorder[i] == rootVal) {
    
            index = i;
            break;
        }
    }

    TreeNode root = new TreeNode(rootVal);
    // 递归构造左右子树
    root.left = build(inorder, ?, ?,
                      postorder, ?, ?);

    root.right = build(inorder, ?, ?,
                       postorder, ?, ?);
    return root;
}

现在postoder和inorder对应的状态如下：

我们可以按照上图将问号处的索引正确填入：

int leftSize = index - inStart;

root.left = build(inorder, inStart, index - 1,
                  postorder, postStart, postStart + leftSize - 1);

root.right = build(inorder, index + 1, inEnd,
                   postorder, postStart + leftSize, postEnd - 1);

综上，可以写出完整的解法代码：

TreeNode build(int[] inorder, int inStart, int inEnd,
               int[] postorder, int postStart, int postEnd) {
    

    if (inStart > inEnd) return null;
    
    // root 节点对应的值就是后序遍历数组的最后一个元素
    int rootVal = postorder[postEnd];
    // rootVal 在中序遍历数组中的索引
    int index = 0;
    for (int i = inStart; i <= inEnd; i++) {
    
        if (inorder[i] == rootVal) {
    
            index = i;
            break;
        }
    }
    // 左子树的节点个数
    int leftSize = index - inStart;
    TreeNode root = new TreeNode(rootVal);
    // 递归构造左右子树
    root.left = build(inorder, inStart, index - 1,
                       postorder, postStart, postStart + leftSize - 1);

    root.right = build(inorder, index + 1, inEnd,
                        postorder, postStart + leftSize, postEnd - 1);
    return root;
}

有了前一题的铺垫，这道题很快就解决了，无非就是rootVal变成了最后一个元素，再改改递归函数的参数而已。

889. 根据前序和后序遍历构造二叉树

889. 根据前序和后序遍历构造二叉树，leetcode链接

函数签名如下：

public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
    };

这道题和前两道题有一个本质的区别：

通过 前序 中序遍历，后序 中序遍历 结果可以确定唯一的二叉树，但是通过前序后序遍历结果无法确定唯一的二叉树。

题目也说了，如果有多种可能的还原结果，你可以返回任意一种。

为什么呢？ 我们之前说过，构建二叉树的套路，无非就是先找到根节点，然后通过跟节点递归构造左右子树即可。

前两道题，可以通过前序或者后序遍历结果找到根节点，然后根据中序遍历结果确定左右子树。

这道题，你可以确定根节点，但是无法确切的知道左右子树有哪些节点。

举个例子，比如给你这个输入：

preorder = [1,2,3], postorder = [3,2,1]

下面这两棵树都是符合条件的，但显然它们的结构不同：

不过话说回来，用后序遍历和前序遍历结果还原二叉树，解法逻辑上和前两道题差别不大，也是通过控制左右子树的索引来构建：

1. 首先把前序遍历结果的第一个元素或后序遍历结果的最后一个元素确定为根节点的值。

2. 然后把前序遍历结果的第二个元素作为左子树的根节点的值。

3. 在后序遍历结果中寻找左子树根节点的值，从而确定了左子树的索引边界，进而确定右子树的索引边界，递归构造左右子树即可。

代码如下：

public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
    
    return build(preorder, 0, preorder.length - 1,
                 postorder, 0, postorder.length - 1);
}

private TreeNode build(int[] preorder, int preStart, int preEnd,
                       int[] postorder, int postStart, int postEnd) {
    
    // 为了要保证索引不越界，必须保证 preStart + 1 <= preEnd，即 preStart < preEnd
    if (preStart > preEnd) return null;
    
    int rootVal = preorder[preStart]; // 根节点值
    int leftRootVal = preorder[preStart + 1]; // 左子树节点值，对于rootVal来说属于左子树
    int index = 0; // leftRootVal的索引
    // 前序遍历数组的第一个元素等于后序遍历最后一个元素
    // 在后序数组中寻找leftRootVal的索引
    for (int i = postStart; i < postEnd; i++) {
    
        if (postorder[i] == leftRootVal) {
    
            index = i;
            break;
        }
    }
    int leftSize = index - postStart + 1; // +1是因为leftRootVal也属于左子树
    TreeNode root = new TreeNode(rootVal);
    root.left = build(preorder, preStart + 1, preStart + leftSize,
                       postorder, postStart, index);
    // index为leftRootVal的索引，作为左子树的边界，所以不用-1
    root.right = build(preorder, preStart + leftSize + 1, preEnd,
                        postorder, index + 1, postEnd - 1);
    // postEnd-1是因为前序遍历数组的第一个元素等于后序遍历最后一个元素
    return root;
}

代码和前两道题非常类似，我们可以看着代码思考一下，为什么通过前序遍历和后序遍历结果还原的二叉树可能不唯一呢？

关键在这一句：

int leftRootVal = preorder[preStart + 1];

我们都知道，一般前序遍历的第二个元素是左子树的根节点，但实际上左子树有可能是空的，那么这个元素就应该是右子树的根节点。由于这里无法确切进行判断，所以导致了最终答案的不唯一。