当前位置:网站首页>深入理解去噪论文——FFDNet和CBDNet中noise level与噪声方差之间的关系探索
深入理解去噪论文——FFDNet和CBDNet中noise level与噪声方差之间的关系探索
2022-04-23 05:44:00 【umbrellalalalala】
知乎同名账号同步发布。如有错误,欢迎指正。
问题来源
读这两篇文章的时候,发现文中AWGN(加性高斯白噪声)的方差用σ²表示,noise level用σ表示,符号使用似乎出现了冲突;
又发现作者默认已知噪声模型 N ( 0 , σ 2 ) N(0, \sigma^2) N(0,σ2),生成的含噪声图像的ground-truth的noise level似乎也随之确定,一切都在暗示AWGN的方差和其noise level有千丝万缕的关系。
一、基础知识和生成AWGN步骤
引用这篇文章对matlab生成AWGN的讲解,补充一些基础知识:
awgn(x,snr,’measured’,'linear’)的作用是向x加入信噪比为snr的AWGN。所谓信噪比,公式如下:
s n r = s i g P o w e r / n o i s e P o w e r snr = sigPower/noisePower snr=sigPower/noisePower
即信号的强度/噪声的强度,或者信号功率/噪声功率。
sigPower的计算方法只需要看matlab代码就一目了然:
sigPower = sum(abs(sig(: )).^2)/length(sig(: ))
(.^2指的是对矩阵每个元素都求平方,上述分母起到规范化的作用,sig(: )表示信号)
awgn()函数的第一步,就是估计信号x的强度sigPower,然后计算出noisePower:
n o i s e P o w e r = s i g P o w e r / s n r noisePower = sigPower / snr noisePower=sigPower/snr
假如说要生成的噪声的size是[1000, 1],那么最终要添加的噪声信号就是:
sqrt(noisePower) * randn(n, 1)
其中randn生成的是 N ( 0 , 1 ) N(0, 1) N(0,1)的噪声,那么这个噪声信号服从的分布就是:
N ( 0 , n o i s e P o w e r ) N(0, noisePower) N(0,noisePower)
所以网上有篇文章,文中一句话说:
对于高斯噪声,其方差和功率(噪声强度)是一样的
二、从MATLAB生成含AWGN的noisy image入手分析
二.0、先放结论
noisePower就是方差σ²,σ就是paper中的noise level。
取自FFDNet paper:对于clean image x,生成noise level为σ的noisy y:
imnoise(x, ’gaussian’, 0, (σ/255)²)
作用就是向x中加入高斯噪声,这个噪声服从的分布为:
N ( 0 , ( σ / 255 ) 2 ) N(0, (\sigma/255)^2) N(0,(σ/255)2)
当然,分母的255可能是因为将原始图片的像素值缩放到了0-1之间,所以noise level也需要除以255。如果没有这样做,那么显然噪声服从的分布就是:
N ( 0 , σ 2 ) N(0, \sigma^2) N(0,σ2)
那么显然,结合目前搜集到的信息,noisePower就是方差σ²,σ就是paper中的noise level。再看一个FFDNet中的片段佐证这个观点:
To synthesize spatially variant AWGN, we first generate an AWGN image v1 with unit standard deviation and a noise level map M of the same size. Then, element-wise multiplication is applied on v1 and M to produce the spatially variant AWGN, i.e., v = v1 ⊙ M.
上述noise level map M就是由不同位置的noise level σ组合而成的map。先生成v1,它拥有单位标准差,然后让M(M中元素为noise level σ)和它做element-wise的相乘,显然得到的v就拥有方差σ²,而论文称σ为noise level,不就和上面的观点对应上了么。
再看CBDNet中所提到:
For a batch of real images, due to the unavailability of ground-truth noise level map, only Lrec and LT V are considered in training.
对于真实数据,是无法得到ground-truth的noise level map的,我当时很疑惑的点在于:对于合成数据,也没有办法得到ground-truth的noise level map,为什么paper似乎在默认这个是能够得到的?然而实际上,paper中提到了合成数据中噪声服从的分布:
N ( 0 , σ 2 ( L ) ) N(0, \sigma^2(L)) N(0,σ2(L))
其中 σ 2 ( L ) = L ⋅ σ s 2 + σ c 2 \sigma^2(L) = L · \sigma^2_s+\sigma^2_c σ2(L)=L⋅σs2+σc2,(L是irradiance image)。
这样,合成数据的ground-truth的noise level map不就直接是 σ ( L ) \sigma(L) σ(L)了么(如果本文之前的推断都没问题的话)。
三、小结
-
确定的事情:
对于高斯噪声,方差σ²就是噪声强度noisePower;
如果已知噪声服从的高斯分布,那么对于根据这个分布+clean image合成的noisy image,可以直接得出其ground-truth的noise level or noise level map。 -
不太确定的事情:
另外读到这里你肯定发现了论文中的noise level和本文中的noisePower不是一个东西,网上没有找到两者特别明显的概念区别,所以noise level可能是作者对σ起的专门的称谓,这个称谓是否为图像去噪领域默认叫法,我还不太清楚。

版权声明
本文为[umbrellalalalala]所创,转载请带上原文链接,感谢
https://blog.csdn.net/umbrellalalalala/article/details/120686861
边栏推荐
- Latex quick start
- 建表到页面完整实例演示—联表查询
- 金蝶EAS“总账”系统召唤“反过账”按钮
- Rsync for file server backup
- Meta annotation (annotation of annotation)
- umi官网yarn create @umijs/umi-app 报错:文件名、目录名或卷标语法不正确
- Software architecture design - software architecture style
- MySQL的锁机制
- 多线程与高并发(3)——synchronized原理
- Pyqy5 learning (III): qlineedit + qtextedit
猜你喜欢

opensips(1)——安装opensips详细流程
Package mall system based on SSM

Pytorch Learning record (XIII): Recurrent Neural Network

Pyqy5 learning (4): qabstractbutton + qradiobutton + qcheckbox

MySQL realizes master-slave replication / master-slave synchronization
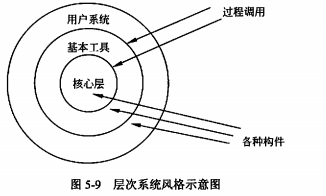
软件架构设计——软件架构风格

Anaconda安装PyQt5 和 pyqt5-tools后没有出现designer.exe的问题解决

Graphic numpy array matrix

给yarn配置国内镜像加速器

Anaconda installed pyqt5 and pyqt5 tools without designer Exe problem solving
随机推荐
JVM系列(4)——内存溢出(OOM)
EditorConfig
创建二叉树
Dva中在effects中获取state的值
The list attribute in the entity is empty or null, and is set to an empty array
JVM series (3) -- memory allocation and recycling strategy
redhat实现目录下特定文本类型内关键字查找及vim模式下关键字查找
MySQL lock mechanism
Navicate连接oracle(11g)时ORA:28547 Connection to server failed probable Oeacle Net admin error
Pyqy5 learning (III): qlineedit + qtextedit
自定义异常类
Ptorch learning record (XIII): recurrent neural network
Pytorch学习记录(九):Pytorch中卷积神经网络
Pytorch learning record (IV): parameter initialization
PyEMD安装及简单使用
域内用户访问域外samba服务器用户名密码错误
你不能访问此共享文件夹,因为你组织的安全策略阻止未经身份验证的来宾访问
2 - principes de conception de logiciels
MySQL的锁机制
SQL基础:初识数据库与SQL-安装与基本介绍等—阿里云天池