From brute force recursion to dynamic programming leetcode Question 62: Different paths

1、什么是动态规划?

动态规划（英语：Dynamic programming,简称 DP）,是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法.动态规划常常适用于有重叠子问题和最优子结构性质的问题.

2、动态规划的核心思想

动态规划的基本思想是将待求解的问题分解成若干个相互联系的子问题,先求解子问题,然后从这些子问题的解得到原问题的解.对于重复出现的子问题,只在第一次遇到的时候对它进行求解,并把答案保存起来,让以后再次遇到时直接引用答案,不必重新求解.

3、leetcode案例分析

**Violent recursive thinking:**For recursion, we have to determine the conditions for recursive return,Because of the problem, the robot can only go forward,Or go to the right,So the first condition for our recursive return is that the robot's position is already greater than thatm或者大于了n,At this time, it means that the robot has not reached the lower right corner,The second recursive condition is when the robot goes to the bottom right,Indicates that a path has been found.
代码实现:

class Solution {
    
public:
    int uniquePaths(int m, int n) {
    
        int i=0,j=0;
        return _uniquePaths(i,j,m-1,n-1);
    }
    int _uniquePaths(int i,int j,int m,int n)
    {
    
        if(i>m||j>n)
          return 0;

        if(i==m&&j==n)
           return 1;

        return _uniquePaths(i+1,j,m,n)+_uniquePaths(i,j+1,m,n);
    }
};

Here I wrote another sub-function to recurse,这里的i和jIt represents the current position of the robot,When the robot has crossed the line,我们直接返回0就可以了,Because of the cross-border situation,No matter how you go, it is impossible to get to the lower right corner,如果说im&&jnIt means we have found a path,返回1即可,Finally repeat this function recursively,_uniquePaths(i+1,j,m,n)It is to calculate all the times that the robot goes right at this time and add it_uniquePaths(i,j+1,m,n)The number of times the robot has moved forward at this time,Return the number of times they add up to the number of times the lower right corner can be reached.
我们的思路是对的,But the question is actually not passable,Because the stack frame of the call is too large,超出了时间限制.
如下:

动态规划解题思路:
We found that if the robot wants to go to the bottom right corner,must go(m-1,n)或者(m,n-1）这两个位置,want to go(m-1,n)This position must be reached again(m-2,n)或者(m-1,n-1),子问题再拆分成子问题,这就是动态规划的核心思想,我们可以创建一个二维数组dp,大小就是m*n这么大,Each location stores the maximum number of different paths the robot takes to that location. Here's a picture for everyone to understand：

First the robot is there(0,0)这个位置,At this time, the robot moves forward in a row of grids,都只有一种走法,At this time, the first line of the robot going to the right has only one way to move,So I filled it all in1,Explain to you why,Because it is impossible to go backward and to the left,So once the robot goes forward,There is no way to go to the first row of grids,Conversely, when the robot goes right,There is no way to get to the first grid.
Next we need to calculate the maximum number of different paths to other grids,而我们可以发现,其实(1,1）The number of times this coordinate is actually able to go(1,0)The number of times plus can go(0,1）的次数,Such a line-by-line calculation,坐标(2,6)The value of is actually the maximum number of different paths that can go to the lower right corner.
代码实现:

class Solution {
    
public:
    int uniquePaths(int m, int n) {
    
        int dp[m][n];
        for(int i=0;i<n;i++)
        {
    
            dp[0][i]=1;
        }
        for(int i=0;i<m;i++)
        {
    
            dp[i][0]=1;
        }
        for(int i=1;i<m;i++)
        {
    
            for(int j=1;j<n;j++)
            {
    
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
};

运行结果如下: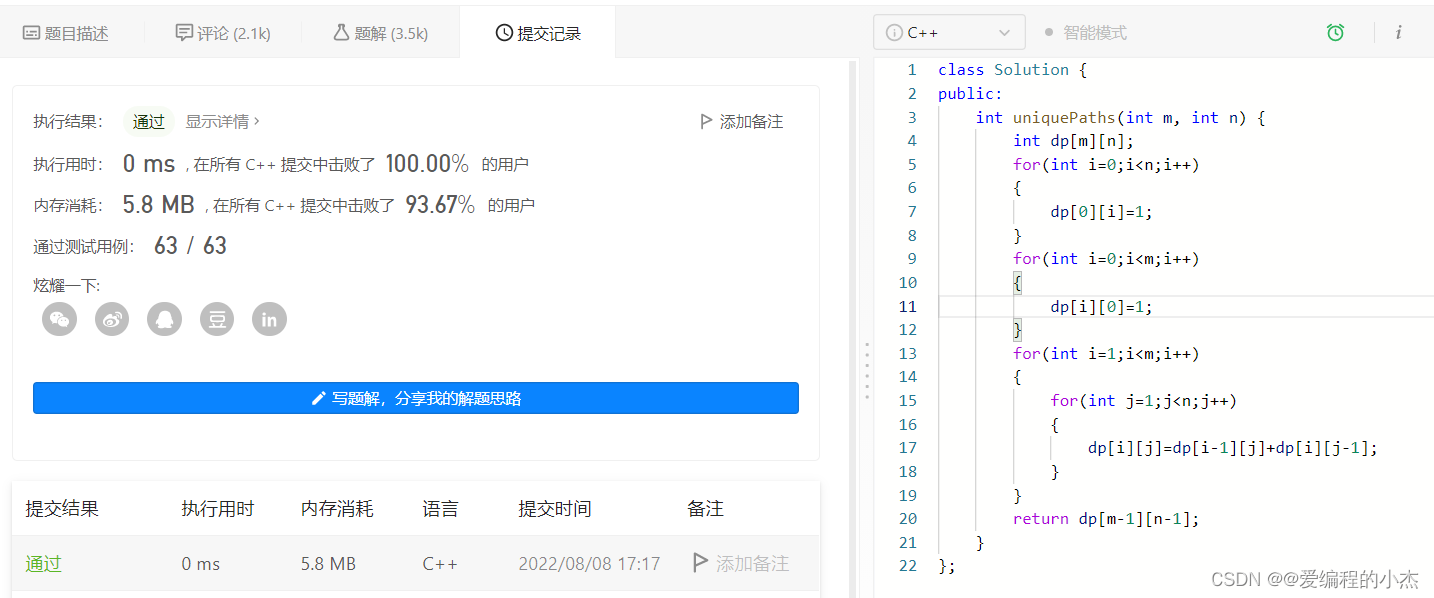

这就是本篇博客的全部内容了,希望对大家有所帮助,感谢大家观看,喜欢的记得点赞收藏加关注哦!I will continue to update this type of questions!