一、模型model

• 一个函数function的集合：

  • 其中w_i代表权重weight，b代表偏置值bias
  • 𝑥_𝑖可以取不同的属性，如: 𝑥_𝑐𝑝, 𝑥_ℎ𝑝, 𝑥_𝑤,𝑥_ℎ…

  $$y=b+\sum w_i{x}_i$$

• 我们将𝑥_𝑐𝑝拿出来作为未知量，来寻找一个最优的线性模型Linear model：
  $$y=b+w\bullet Xcp$$

二、较好的函数function

• 损失函数Loss function 𝐿：

  • L的输入Input是一个函数 f ，输出output则是一个具体的数值，而这个数值是用来评估输入的函数 f 到底有多坏

  • ${\hat{y}}^n$代表真实值，而$f(x_{cp}^n)$代表预测值，$L(f)$代表真实值与预测值之间的总误差
    $$L(f)=\sum _{n=1}^{10}({\hat{y}}^n-f(x_{cp}^n){)}^2$$

  • 将函数 f 用w，b替换，则可以写成下面这样
    $$L(w,b)=\sum _{n=1}^{10}({\hat{y}}^n-(b+w\cdot x_{cp}^n){)}^2$$

  • 当 L 越小时，则说明该函数 f 越好，也就是该模型越好。在下图中的每一个点都代表一个函数 f

    

三、最好的函数function

• 梯度下降Gradient Descent：就是求最好函数的过程

• $f^{ } $代表最好的函数function，$w^{*},b{ }：$代表最好的权重weight和偏置值bias

  $f^{\ast }=arg\underset{f}{\min }L(f)$

  $w^{\ast },b^{\ast }=arg\underset{w,b}{\min }L(w,b)$

  ​ $=arg\underset{w,b}{\min }{\sum }_{n=1}^{10}({\hat{y}}^n-(b+w\cdot x_{cp}^n){)}^2$

3.1 一维函数

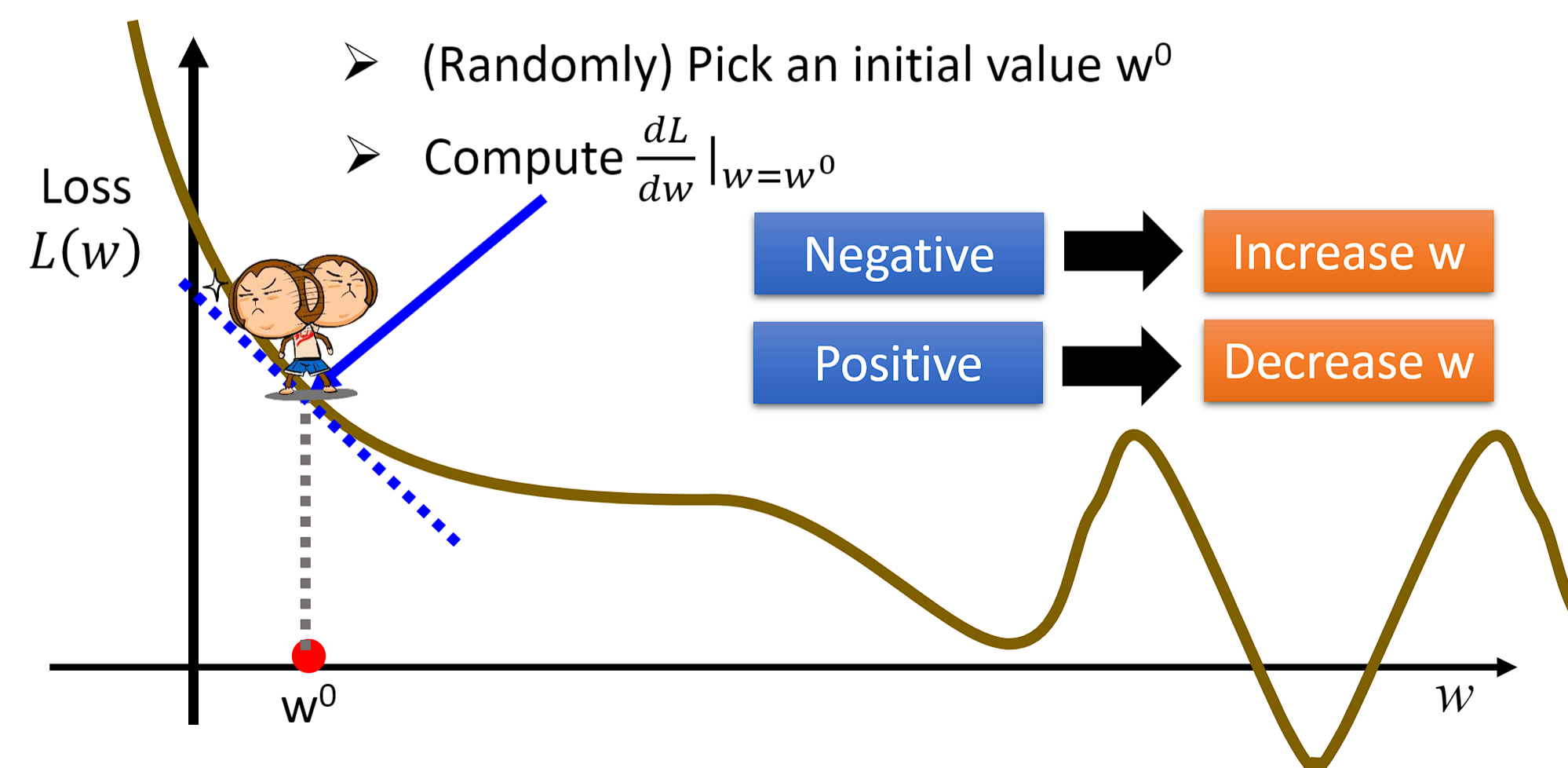
下图代表Loss函数求梯度下降（Gradient Descent）的过程，首先随机选择一个$w^0$。在该点对w求微分，如果为负数，那么我们增大$w^0$的值；如果为正数，那么我们减小$w^0$的值。

• $w^{\ast }=arg\underset{w}{\min }L(w)$
• $w^0=-\eta \frac{dL}{dw}{|}_w$，其中 η 代表学习率：Learning rate，意味着每次移动的步长（step）
• $w^1\leftarrow w^0-\eta \frac{dL}{dw}{|}_{w=w^0}$，$w1$代表初始点$w^0$要移动的下一个点，就这样一直迭代（Iteration）下去，最终就会找到我们的局部最优解：Local optimal solution

3.2 二维函数

• 对二维函数$Loss $ $L(w,b)$求梯度下降：${\left[\begin{array}{c}\frac{\partial L}{\partial w}\\ \frac{\partial L}{\partial b}\end{array}\right]}_{gradient}$
• $w^{\ast },b^{\ast }=arg\underset{w,b}{\min }L(w,b)$
• 随机初始化$w^0,b^0$，然后计算$\frac{\partial L}{\partial w}{|}_{w=w^0,b=b^0}$和$\frac{\partial L}{\partial b}{|}_{w=w^0,b=b^0}$：
  • $w^1\leftarrow w^0-\eta \frac{\partial L}{\partial w}{|}_{w=w^0,b=b^0}$
  • $b^1\leftarrow b^0-\eta \frac{\partial L}{\partial b}{|}_{w=w^0,b=b^0}$

3.3 局部最优解和全局最优解

• 公式化（Formulation）$\frac{\partial L}{\partial w}$和$
  \frac{\partial L}{\partial b}$：

  • $L(w,b)={\sum }_{n=1}^{10}({\hat{y}}^n-(b+w\cdot x_{cp}^n){)}^2$
  • $\frac{\partial L}{\partial w}=2{\sum }_{n=1}^{10}({\hat{y}}^n-(b+w\cdot x_{cp}^n))(-x_{cp}^n)$
  • $\frac{\partial L}{\partial b}=2{\sum }_{n=1}^{10}({\hat{y}}^n-(b+w\cdot x_{cp}^n))$

• 在非线性系统中，可能会存在多个局部最优解：

  

3.4 模型的泛化（Generalization）能力

• 将根据loss函数找到的最好模型拿出来，分别计算它在训练集（Training Data）和测试集（Testing Data）上的均方误差（Average Error），当然我们只关心模型在测试集上的具体表现如何。

  • $y=b+w\bullet x_{cp}$ Average Error=35.0

• 由于原来的模型均方误差还是比较大，为了做得更好，我们来提高模型的复杂度。比如，引入二次项(x_cp)²

  • $y=b+w1\bullet x_{cp}+w2\bullet (x_{cp)}2$ Average Error = 18.4

• 继续提高模型的复杂度，引入三次项(x_cp)³

  • $y=b+w1\bullet x_{cp}+w2\bullet (x_{cp})2+w3\bullet (x_{cp})3$ Average Error = 18.1

• 继续提高模型的复杂度，引入三次项(x_cp)⁴，此时模型在训练集上的均方误差变得更小了，但测试集上的反而变大了，这种现象被称为模型的过拟合（Over-fitting）

  • $y = b + w1∙x_{cp} + w2∙(x_{cp})2+ w3∙(x_{cp})3+ w4∙(x_{cp})4 $ Average Error = 28.8

3.5 隐藏的因素（hidden factors）

• 当我们不仅仅只考虑宝可梦的cp值，将宝可梦的物种因素也考虑进去的话，在测试集上的均方误差降低到了14.3

• 当我们继续考虑其他的因素，比如每只宝可梦的身高Height，体重weight，经验值HP。模型此时变得更加复杂了，让我们来看看它在测试集上的具体表现如何，非常不幸模型再次出现过拟合。

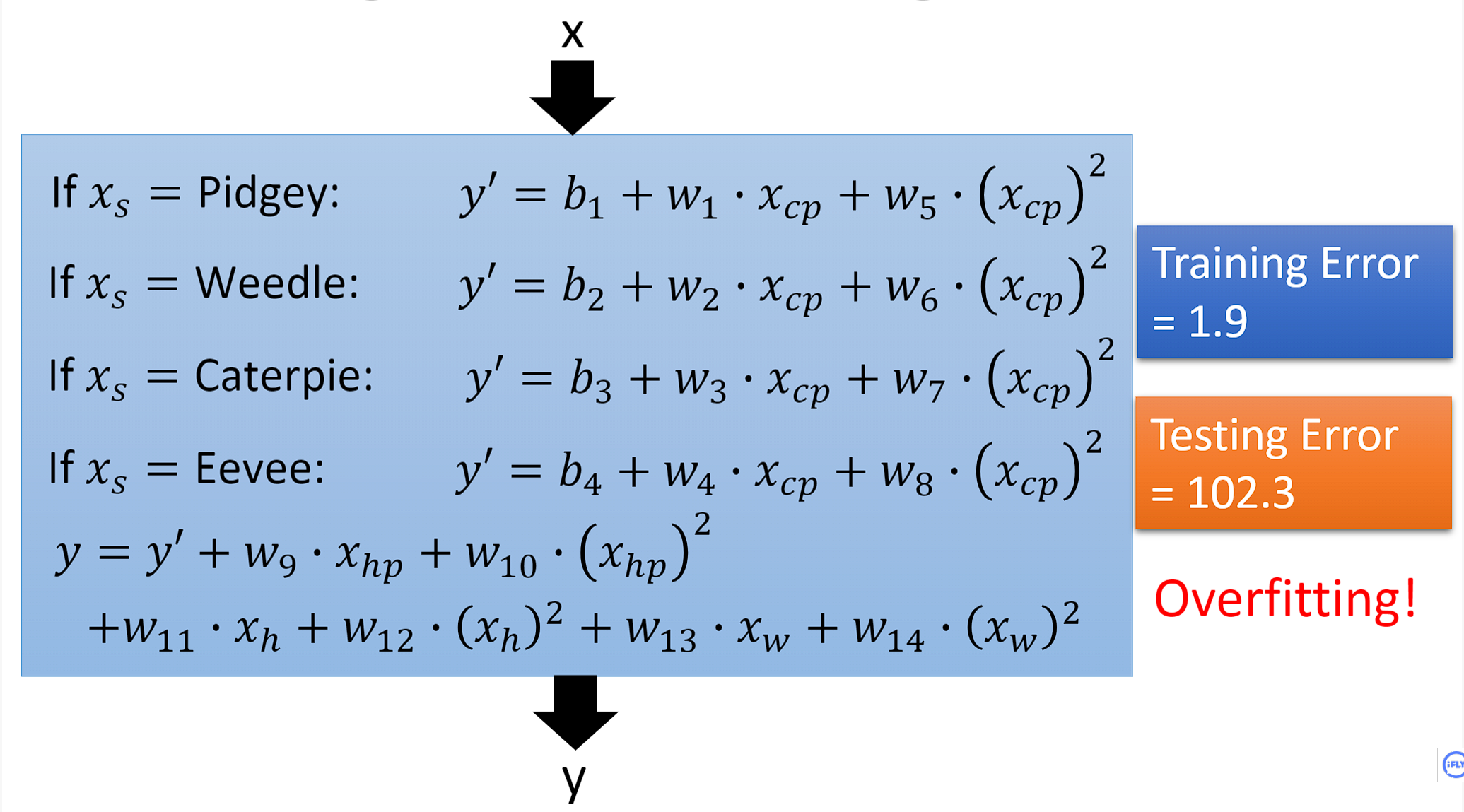
3.5 正则化（Regularization）

• 为了解决过拟合的问题，我们需要重新设计一下损失函数 L，原来的损失函数只计算了方差，而没有考虑到含有干扰的输入对模型的影响。因此我们在 L 后面加上一项: $\lambda \sum (w_i{)}^2$ ，以此来提高模型的泛化能力，使模型变得更加平滑，降低模型对输入的敏感（Sensitive）

  • 重新设计的损失函数 L ：$L(f)=\sum _n({\hat{y}}^n-(b+\sum w_i{x}_i){)}^2+\lambda \sum (w_i{)}^2$

• 很显然根据下面的实验，我们取得了更好的表现，$当\lambda =100时，TestError=11.1$